
CAP-DSDN: Node Co-association Prediction in Communities in Dynamic
Sparse Directed Networks and a Case Study of Migration Flow
Jaya Sreevalsan-Nair
1 a
and Astha Jakher
2
1
Graphics-Visualization-Computing Lab, International Institute of Information Technology Bangalore, Bangalore, India
2
Department of Humanities and Social Sciences, IIT Kharagpur, Kharagpur, West Bengal 721302, India
Keywords:
Real-world Graphs, Directed Networks, Edge Sparsity, Dynamic Networks, Community Detection,
Community Evaluation, Migration Flows, Co-association, Prediction, Autoregressive Models, VAR Model,
ARMA Model.
Abstract:
Predicting the community structure in the time series, or snapshots, of a real-world graph in the future, is a
pertinent challenge. This is motivated by the study of migration flow networks. The dataset is characterized
by edge sparsity due to the inconsistent availability of data. Thus, we generalize the problem to predicting
community structure in a dynamic sparse directed network (DSDN). We introduce a novel application of co-
association which is a pairwise relationship between the nodes belonging to the same community. We thus
propose a three-step algorithm, CAP-DSDN, for co-association prediction (CAP) in such a network. Given
the absence of benchmark data or ground truth, we use an ensemble of community detection (CD) algorithms
and evaluation metrics widely used for directed networks. We then define a metric based on entropy rate as
a threshold to filter the network for determining a significant and data-complete subnetwork. We propose
the use of autoregressive models for predicting the co-association relationship given in its matrix format. We
demonstrate the effectiveness of our proposed method in a case study of international refugee migration during
2000–18. Our results show that our method works effectively for migration flow networks for short-term
prediction and when the data is complete across all snapshots.
1 INTRODUCTION
The communities in the time series of directed net-
works (Malliaros and Vazirgiannis, 2013) enable us
to understand the change in the network topology in
real-world graphs. Let us take the example of the in-
ternational refugee migration network. Using the mi-
gration flow data for n consecutive years, referred to
as snapshots, we get the time series of a directed net-
work, where the countries are nodes and the migrant
counts are the edge weights. Predicting a network at a
future time is difficult as it involves predicting the oc-
currence of edges, i.e., pairwise relationship between
nodes, and their weights. This issue deteriorates in the
case of edge-sparse networks where there is no spe-
cific known model for the occurrence of edges. For
instance, in the case of migration networks, there are
socio-economic-political systemic dependencies, nat-
ural disasters, and other factors for the additions and
deletions of nodes and edges in the network which are
often complex to predict (Suleimenova et al., 2017).
a
https://orcid.org/0000-0001-6333-4161
At the same time, the data is not consistently avail-
able for any given pair of countries owing to lapses in
data curation and communication (Neumayer, 2005).
This inconsistency in the availability of edge data also
leads to inaccuracy in the study of network commu-
nity structures. Hence, we shift our focus to studying
the community behavior of nodes in the network in-
stead of the communities themselves. Thus, we focus
on using the persistent community behavior of nodes
in the time series to predict its community behavior
in the future. We propose an algorithm, CAP-DSDN
1
(Co-Association Prediction in Dynamic Sparse Di-
rected Network), for predicting the co-association be-
tween nodes in the (n+1)
th
year, using the data until
the n
th
year.
As an example, if the United States of America
(USA) and Mexico co-existed in a community over
most part of the n-year period, can we then use the
available data to predict their co-association in a com-
munity, i.e., membership to the same community,
in the (n+1)
th
year? Our proposed algorithm, CAP-
1
Pronounced as \kap-duhs-durn\.
Sreevalsan-Nair, J. and Jakher, A.
CAP-DSDN: Node Co-association Prediction in Communities in Dynamic Sparse Directed Networks and a Case Study of Migration Flow.
DOI: 10.5220/0011537600003335
In Proceedings of the 14th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2022) - Volume 1: KDIR, pages 63-74
ISBN: 978-989-758-614-9; ISSN: 2184-3228
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
63

DSDN (Figure 1) predicts such co-associations at a
future time instance, which in turn helps in inferring
the community structure. It must be noted that CAP-
DSDN does not predict the number of communities or
their constituencies. Instead, CAP-DSDN predicts the
likelihood of any two nodes being in the same com-
munity in the future.
Our novel contributions towards community anal-
ysis in DSDNs are:
• A three-step algorithm, CAP-DSDN, for co-
association prediction (CAP) for implicitly fore-
casting community behavior in real-world graphs
which are DSDNs.
• Definition of a metric of entropy rate H to be
used on the co-association matrices (CAM) for
determining persistent community behavior of the
nodes, and thus, a threshold τ
h
for node-filtering
the network to address the issue of sparsity.
• A method of applying time series autoregressive
models to CAMs.
2 RELATED WORK
Recently, the communities in DSDNs have been mod-
eled as routed activity-driven networks for model-
ing its community structure (Bongiorno et al., 2019).
Here, starting from a set of existing community de-
tection (CD) algorithms, such as Louvain, Infomap,
etc., the communities are improved by using the pro-
posed characterization. A recent study on the state-
of-the-art CD algorithms for dynamic networks has
shown that the choice of algorithm is contextual and
is based on the nature of communities and commu-
nity events involved in such networks (Rossetti and
Cazabet, 2018).
In the classification of different CD algo-
rithms (Rossetti and Cazabet, 2018), CAP-
DSDN falls in the category of instant optimal
CD approach that finds communities in each snapshot
and matches communities across snapshots. A known
disadvantage of this approach is that it is ambiguous
if the evolution in community structures is due to the
actual evolution of events or due to the instabilities of
CD algorithms in each timestamp.
There has been an empirical comparison of CD al-
gorithms for directed networks (Agreste et al., 2016),
which has studied the accuracy and time complex-
ity of selected state-of-the-art methods on real and
synthetic datasets. This work has concluded that
the WalkTrap algorithm (Pons and Latapy, 2006)
has the highest accuracy, but the worst time com-
plexity. The other key algorithms discussed in this
work are Infomap (IMAP) (Rosvall and Bergstrom,
2008), eigenvector algorithm or the modularity opti-
mization for directed networks (MODN) (Leicht and
Newman, 2008), and speaker-listener label propaga-
tion algorithm (SLPA) (Xie et al., 2011). The al-
gorithms are further classified as follows, based on
how they use the directionality information of the
networks: (i) directionality-preserving ones, e.g., In-
fomap and label propagation algorithm, and (ii)
directionality-discarding ones, e.g., eigenvector algo-
rithm and WalkTrap.
SLPA is based on directional propagation of la-
bels, whereas MODN defines a community based on
high and low densities of intra- and inter-community
edges, respectively; and IMAP uses random walks to
determine communities. Thus, these methods fall in
different categories of models used for CD, namely,
models based on dynamic processes on graphs, on a
null model, and on a flow model, respectively (Agreste
et al., 2016). SLPA and IMAP are efficient methods
and scalable to large graphs (Agreste et al., 2016).
SLPA and IMAP methods use the directionality infor-
mation, whereas MODN ignores the same by using a
symmetric adjacency matrix.
• Speaker Listener Label Propagation Algorithm
(SLPA) (Xie et al., 2011): is an extension of
the label propagation algorithm which initially as-
signs each node with a unique label and iteratively
updates labels to the most frequently occurring la-
bel in the neighborhood of the node. SLPA ex-
tends to overlapping communities, where nodes
can have multiple labels based on their role as a
listener or a speaker.
• Modularity Optimization for Directed Networks
(MODN) Algorithm (Leicht and Newman, 2008):
uses the variant of Girvan-Newman modularity
for directed networks, given by:
Q =
1
2m
∑
i, j
A
i, j
−
k
i
k
j
2m
δ(C
i
,C
j
),
where A
i j
is an element of the adjacency matrix
A giving edge weight between nodes i and j,
δ
i j
is the Kronecker delta, C
i
is the label of the
community to which node i belongs, k
i
is the
degree of node i, and 2m is the sum of degrees
of all nodes in the network. The algorithm is
implemented as an optimization problem, where
Q is maximized for community detection. The
maximum value of Q is considered as the best
approximation of the true communities in the
network.
• Infomap (IMAP) Algorithm (Rosvall and
Bergstrom, 2008): is based on information
theory, using the map equation. The entropy
of random walks within and between modules
KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval
64
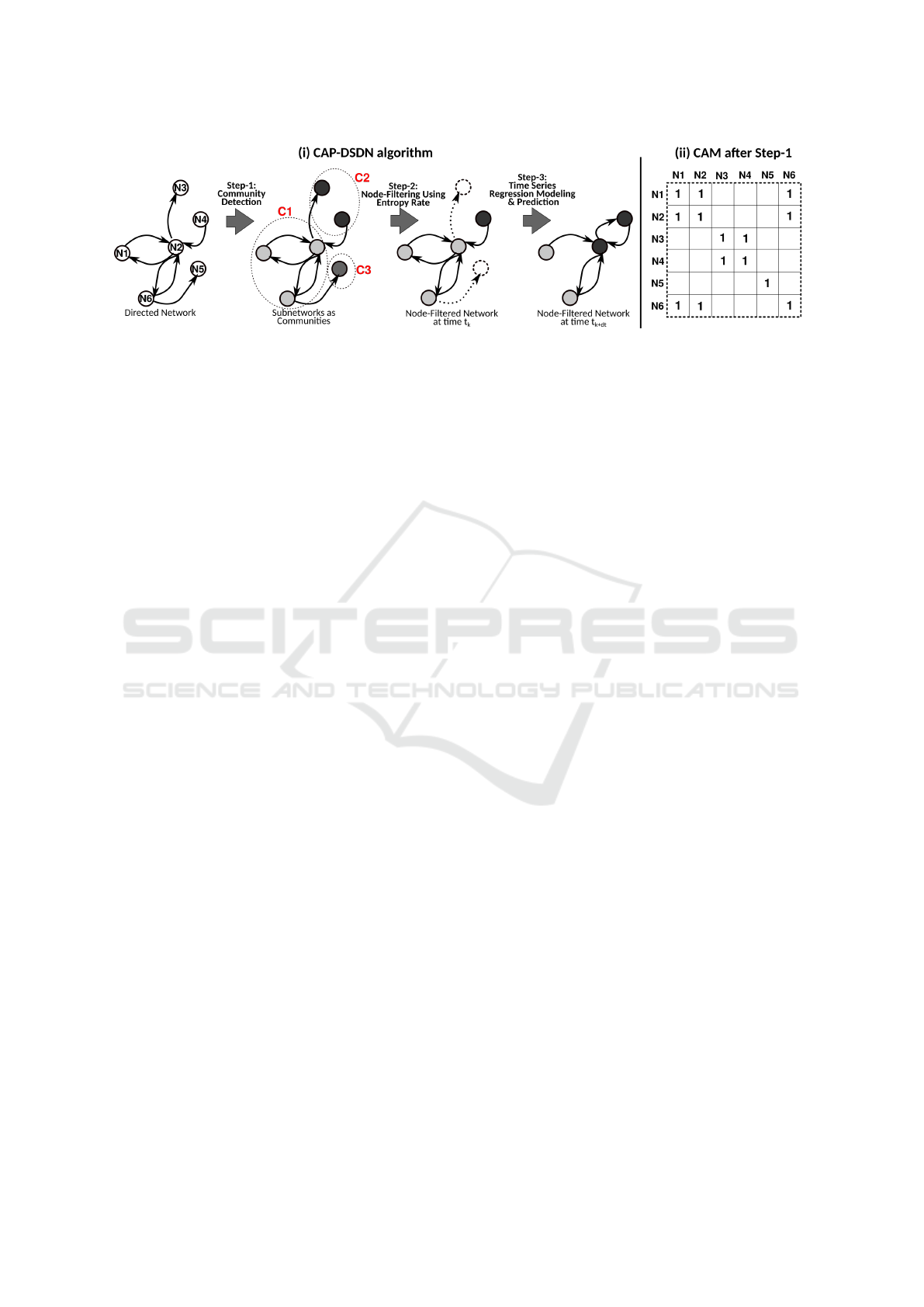
Figure 1: (i) Our proposed three-step algorithm, CAP-DSDN, for prediction of community behavior of nodes in a dynamic
sparse directed network (DSDN), where the node color indicates community ID. (ii) The co-association matrix (CAM) of the
network after community detection (CD) in Step-1.
is used in a cost function in the map equation.
This cost function is the expected description
length of a random walk, which is minimized.
Thus, the best node-partitioning occurs where the
probability flow is the most cost-efficient.
Community detection has been recently implemented
on sparse directed networks using a parameter-Sparse
Random Graph Model, that preserves the direction-
ality (Stein and Leng, 2021). This involves model-
ing using an estimator using an l
1
penalty to achieve
sparsity in parameter space to simulate a sparse net-
work. Previously, spectral methods have been used
extensively for sparse directed networks using the
spectrum of the non-backtracking matrix (Singh and
Humphries, 2015; Krzakala et al., 2013). Spec-
tral methods using non- and reluctant-backtracking
matrices have been successfully used for real-world
graphs (Singh and Humphries, 2015).
Perturbing and resampling network has been done
to aggregate information in large sparse undirected
networks (Mirshahvalad et al., 2012). This is simi-
lar to our proposed method of using an information-
theoretic metric of entropy rate for assessing the sta-
tistical significance of communities. The size of a
controllable subnetwork for a node has been used to
determine the statistical significance of the node in
sparse directed networks (Wang et al., 2012). This is
similar to how we use moving average smoothing for
finding significant nodes.
There is limited work on community detection
in dynamic sparse directed networks (DSDNs). Re-
cently, a consensus method has been used to deter-
mine the state of clusters of nodes (Martin et al.,
2016). The rationale for tracking the state of the node
clusters is for reducing the dimensionality of DSDNs.
Our work is different, as we are focused on predicting
co-association values, so as to not limit our analysis
to the raw network data alone.
3 PRELIMINARIES
Here, we define the Co-association Matrix (CAM)
and persistent community behavior.
Definition 1. A Co-association Matrix (CAM) is a
symmetric matrix with rows and columns represent-
ing the same set of data items, say countries in the
migration flow network, in the same order, and each
cell (i, j) indicates if the item in the i
th
row and that
in the j
th
column are associated with the same clus-
ter, i.e., belong to the same community in the case of
networks.
Definition 2. Persistent Community Behavior is a
property of a node of a dynamic network where it
has a high likelihood of non-zero co-association with
other nodes in a network across several snapshots.
4 CAP-DSDN: OUR PROPOSED
METHOD
Our three-step algorithm, CAP-DSDN, is as follows:
Step-1: Perform community detection in each snap-
shot of a DSDN using an ensemble of CD algorithms
and compute an aggregated CAM.
Step-2: Determine a subnetwork of nodes with
persistent community behavior using the aggregated
CAM, thus implementing node-filtering the network.
Step-3: Perform time series autoregressive models
on the CAM of the filtered network to predict the
community structure in the subnetwork in the future.
To handle the limitations of analysis stemming
from the sparsity in the networks, our approach is to
localize our analysis to a subnetwork that shows per-
sistent community behavior. Thus, we further analyze
a relatively denser subnetwork, which is determined
using the preprocessing steps Step-1 and Step-2. The
CAP-DSDN: Node Co-association Prediction in Communities in Dynamic Sparse Directed Networks and a Case Study of Migration Flow
65

requirement of a dense network also comes from the
insufficiency of data for a prediction algorithm.
We predict the co-association between nodes of
the network instead of the edge weight as the co-
association value has the property of being bounded
between 0 and 1, unlike the edge weight. The pre-
dicted co-association value is the probability or likeli-
hood of two nodes belonging to the same community
in the future using their past behavior. Since the com-
munity behavior is computed independently in each
snapshot with the information from the neighboring
snapshots, we now use the concept of moving aver-
age to compute the probability of co-association us-
ing a shorter time window, e.g., five snapshots, as
explained in Section 4.1.
We also do not pursue the idea of predicting the
likelihood of the occurrence of an edge in this work,
as the networks of interest are weighted networks and
not binary ones.
4.1 Step-1: Community Detection
In this step, we compute a CAM for each snapshot of
the network. The inputs to this step are a DSDN and
a CD algorithm, and the outputs are a time series of
community IDs for the nodes.
A community structure selected from an ensem-
ble of methods based on its performance is a reliable
choice in the absence of ground truth in real-world
graphs. Thus, the crux of this step is in identifying
an appropriate CD algorithm for DSDNs. Based on
a literature survey on widely used algorithms for CD
in directed networks (Agreste et al., 2016), we have
selected three algorithms, namely, Speaker-Listener
Label Propagation Algorithm (SLPA), modularity op-
timization for directed networks (MODN), and In-
fomap algorithm (IMAP). These algorithms are de-
signed using different approaches, as explained in
Section 2, which make them suitable for comparative
analysis in our work.
Choice of CD Algorithm: We choose a CD algo-
rithm for a DSDN using the following strategies:
• Community Quality Metrics: We compute the
quality of node-partitioning to form communities
using selected community quality metrics. We
then consider an algorithm to be better performing
when its outcomes are closer to the best quality.
• Characteristics of CD Outcomes in the Time Se-
ries: We consider an algorithm to be better per-
forming if it has consistently created more than
one community across snapshots. An algorithm
that leads to under- or over-fragmentation is not
preferred, which avoids scenarios of monolithic
and overly fragmented communities, respectively.
We identify widely used metrics using a literature
survey and use the following six metrics in this work,
namely, link modularity (LM) (Nicosia et al., 2009),
internal edge density (IED) (Radicchi et al., 2004),
average internal degree (AID) (Radicchi et al., 2004),
cut ratio (CR) (Fortunato, 2010), and Z-modularity
(ZM) (Miyauchi and Kawase, 2016). It is important
to use appropriate metrics for validation, given the
absence of benchmark datasets with ground truth in
real-world graphs. Hence, the final set is identified
based on the better performance of the CD algorithm
on these metrics for our case study.
Computing CAMs: The CAM captures the ten-
dency of any two given nodes belonging to the
same community/cluster/node-grouping. The co-
association relationship between nodes i and j be-
longing to communities C
i
and C
j
, respectively, at
time instance T , is captured in the following matrix
element in CAM:
D
i j
(T ) =
(
1 , if (C
i
(T ) = C
j
(T )) and (i 6= j),
0 , otherwise.
(1)
Probability of Co-association Matrices (PCAMs):
For incorporating the temporal context, CAMs of con-
secutive snapshots can now be averaged to obtain a
probability matrix (or transition matrix), thus, giv-
ing the likelihood of each pair of nodes belonging
to the same community for those years. We refer to
this matrix as the probability of co-association matrix
(PCAM), which is computed by averaging the CAMs
in the moving time-window ∆
T
, and hence referred to
as P(T, ∆
T
). Thus, the probability of co-association
between nodes i and j at time instance T , using val-
ues backward in time, is:
P
i j
(T, ∆
T
) =
1
∆
T
T
∑
t=T −∆
T
+1
D
i j
(t). (2)
Thus, CAM has binary values ‘0’ and ‘1’, and PCAM
has real values in [0,1]. We further use the PCAMs
for the prediction model in Step-3 (Section 4.3).
4.2 Step-2: Node-filtering the Network
Given the quadratic complexity of CAM with an at-
tribute set of size N
a
, we observe that (N
a
N
T
), for
N
T
time instances in real-world graphs. Hence, any
time series analysis runs into the risk of over-fitting.
Thus, given the edge sparsity of the network, there
is a requirement to reduce N
a
. We achieve this by
retaining the significant nodes with highly persistent
community behavior. Such nodes demonstrate a high
tendency to be part of a sufficiently large community
through most of the period of interest. We pay at-
tention to the size of the communities to which these
KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval
66

nodes belong so that we filter out overly fragmented
i.e., small communities. We choose node-filtering
over edge-filtering here because, though the filtering
occurs in the CAM which represents relationships be-
tween nodes, it must also be simultaneously applied
to the original directed network. CAM is equivalent
to an undirected co-association network but uses the
same node-set as the original network. Thus, we fil-
ter the nodes instead of the edges to simultaneously
apply it on both the CAM and the original DSDN.
Defining a Metric for Threshold: Entropy Rate:
The persistence of the co-associations in a network
gives the temporal significance of the relationship be-
tween nodes, which is computed using the time series
of the probability values in PCAMs. Here, we are
interested in the temporal significance of the nodes
to decide if the node is to be filtered out or retained.
Hence, we compute the significance of the node using
the persistence of its co-associations in the network.
To compute the node-wise significance, we first
average the PCAMs over a specific period and then
average across either the rows or the columns, since
it is a symmetric matrix. Thus, for each node i in a
network of n nodes, its probability of associating with
other nodes in the window of time (T −∆
T
, T ], is:
p
i
(T, ∆
T
) =
1
(n − 1)
·
n
∑
j=1
P
i j
(T, ∆
T
). (3)
We use the averaging operator here instead of other
statistical operators, as the average gives us a likeli-
hood or probability value. We can now also see that
for each node i, the (N
T
− ∆
T
+ 1) instances of these
probability values is effectively the moving average
smoothing of the degree of the node in the CAM, for
a window of size ∆
T
. Hence, this operation is a mov-
ing average of order ∆
T
or ∆
T
-MA.
The ∆
T
-MA sequence is derived from a time se-
ries, and hence, is a stochastic process, by design. The
time series of edge weights of a real-world graph is a
stationary process (Cai et al., 2016), and hence the
∆
T
-MA sequence of PCAM elements is also a sta-
tionary process. For a stochastic process of n random
variables, its entropy rate gives us a measure of how
the entropy of the sequence grows with n (Cover and
Thomas, 2006). In our case, the entropy rate of the
sequence of probability values at each node gives us
the change in the tendency of the node to co-associate
with other nodes in communities.
The entropy rate of the stochastic process X is
given by the limiting value of the joint entropy of the
m members of the process {X
1
, X
2
, . . . , X
m
}:
H(X ) = lim
m−>∞
1
m
H(X
1
, X
2
, . . . , X
m
)
For a discrete case of joint entropy, the joint en-
tropy of a set of random variables is bounded by the
sum of entropy of the individual variables (Cover and
Thomas, 2006):
H(X
1
, X
2
, . . . , X
m
) ≤
m
∑
i=1
H(X
i
) =
m
∑
i=1
(−p
i
log(p
i
)).
Thus, we get the upper bound of entropy rate at
each node i, for time sequence (t
1
, . . . , t
∆
T
, . . . , t
N
T
)
as a function of window size ∆
T
for moving average
smoothing:
H
i
(∆
T
) =
N
T
∑
k=∆
T
−(p
i
(t
k
, ∆
T
)log(p
i
(t
k
, ∆
T
)). (4)
Choice of Threshold for Node-filtering: We observe
that the entropy rate of a node i, H
i
, is closer to 0 when
the node is highly likely to co-associate with other
nodes, i.e., p
i
(t
k
, ∆
T
)≈1 across all snapshots. Thus,
the entropy rate for a node H
i
is inversely proportional
to the likelihood of its persistent community behavior.
Hence, we identify a threshold for H
i
, where nodes
with an entropy rate higher than the threshold are fil-
tered out.
We propose to determine the threshold, τ
h
, using a
line plot of sorted entropy rates of all the nodes in the
network and the size of the node-filtered network. A
steep increase in the entropy rate at a transition point
τ
h
implies that the network maintains low entropy un-
til this point. We observe that the real-world graph
tends to have two groups of nodes that correspond to
low and high entropy rates, where the presence of any
node from the latter tends to sharply increase the size
of the node-filtered network.
In the node-filtered network of n
0
nodes, we now
have N
0
a
=
n
0
(n
0
−1)
2
attributes. Since (N
0
a
< N
a
), we
reasonably reduce the gap between N
0
a
and N
T
, even
though (N
0
a
N
T
). We also compute the reduced
PCAM, P
0
(T, ∆
T
), which is a submatrix of the origi-
nal PCAM, P, corresponding to the retained n
0
nodes.
4.3 Step-3: CAP using Autoregressive
Models
We now have time series of N
0
a
attributes in the re-
duced PCAMs, with N
T
time instances each, for the
network. In the case of real-world graphs, we ob-
serve that these attributes, which are the probabil-
ity of co-association values in PCAM, have constant
first moments, i.e., mean, and finite second moments,
i.e., variance. Hence, we can now assume that each of
these N
0
a
attributes in PCAM forms a weakly station-
ary process. Autoregressive models (AR) (Box and
Jenkins, 1970) and their variants are widely used with
time series data for the prediction of weakly station-
ary stochastic processes.
Data Formats of PCAMs: Given that co-association
is a symmetric relationship, the PCAM stores
CAP-DSDN: Node Co-association Prediction in Communities in Dynamic Sparse Directed Networks and a Case Study of Migration Flow
67

Input : A sequence of snapshots of a dynamic sparse directed network (DSDN) in the form of sets {V, E(T
1
),
E(T
2
), . . ., E(T
N
T
)}
Input : Moving-average window ∆
T
, Choice of data format F (i.e., vector-format or independent-attribute-format)
Input : Parameters for the autoregressive model (i.e., p for VAR for vector-format, or (p, q) for ARMA for
independent-attribute-format)
Output: Probability of Co-association Matrix (PCAM) of significant subnetwork P
0
(N
T
+ 1, ∆
T
) (i.e., reduced
PCAM)
// Step-1
for method M in E
CD
(an ensemble of community detection algorithms) do
for 1 ≤ T ≤ N
T
do
A community set C(M) ← Implement(M,{V, E(T )})
Compute the CAM, D(T ), from C, using Equation 1
end
for ∆
T
≤ T ≤ N
T
do
Compute the PCAM, P(T, ∆
T
), using Equation 2
for 1 ≤ i ≤ n do
Compute p
i
(T, ∆
T
) using Equation 3// Likelihood of a node to be co-associated
end
end
end
Select optimal CD method M
opt
based on quality of C(M), cardinality of kCk size of communities
// Step-2
for 1 ≤ i ≤ n do
Compute H
i
(∆
T
) using p
i
from M
opt
, using Equation 4
end
Sort H
i
for all nodes and determine transition point as threshold τ
h
V’ = {} // Node set of the node-filtered network
for 1 ≤ i ≤ n do
if H
i
< τ
h
then
V
0
← V
0
∪ {i}
end
end
for ∆
T
≤ T ≤ N
T
do
P
0
(T, ∆
T
) ← Submatrix of P(T, ∆
T
) for {V
0
,E(T − ∆
T
),E(T − ∆
T
+ 1), . . ., E(T )}// Reduced PCAM
end
// Step-3
if F is (vector-format) then
for ∆
T
≤ T ≤ N
T
do
v(T ) ← half-vectorization of P
0
(T, ∆
T
)
end
v(N
T
+ 1) ← Implement (VAR(p),{v(∆
T
), v(∆
T
+ 1), . . . v(N
T
)}), using Equation 5 // Predict for the
reduced PCAM
end
else if F is (independent-attribute-format) then
v(N
T
+ 1) ← []
for 1 ≤ i ≤ kV
0
k do
for ∆
T
≤ T ≤ N
T
do
Compute p
i
(T, ∆
T
) from P
0
(T, ∆
T
) using Equation 3
end
v
i
(N
T
+ 1) ← Implement(AR(p,q),{p
i
(∆
T
, ∆
T
), p
i
(∆
T
+ 1, ∆
T
), . . . , p
i
(N
T
, ∆
T
)}), using
Equation 6// Predict for each node
v(N
T
+ 1) ← Append(v(N
T
+ 1), v
i
(N
T
+ 1))
end
end
P
0
(N
T
+ 1, ∆
T
) ← Reverse-process of half-vectorization(v(N
T
+ 1))
Algorithm 1: The complete algorithm of CAP-DSDN for DSDNs for prediction of co-association of nodes in a subnetwork
with persistent community behavior.
KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval
68

N
a
=
n(n−1)
2
unique pairwise relationships in a network
of n nodes. We propose to use these co-association
values as attributes in a data model for the predic-
tion of community structure using the autoregressive
models. This leads to two possibilities of using the
attributes from the PCAM: (i) in the form of a vec-
tor, thus modeling a time series of N
a
-long vector, or
(ii) as independent attributes, thus, getting N
a
separate
time series. We use the upper or the lower triangular
part of the PCAM, without the diagonal for generating
(i) and (ii). Thus, we use half-vectorization of PCAM
for (i).
Prediction using Autoregressive Models: Here, we
choose two such models to suit the aforementioned
data formats, namely, (i) the vector auto-regressive
(VAR) model (Sims, 1980) for the vector format of
the attributes, and (ii) the auto-regressive-moving-
average (ARMA) model (Box and Jenkins, 1970) for
the format of the independent attributes.
In the VAR model, for a vector y of length k, con-
stants vector c, k × k matrices as coefficients A
i
, a
vector ε as error term, and p as the order of auto-
regressive model, which is the number of time-lags,
the predicted value is given as:
y(T ) = c +
p
∑
i=1
A
i
y(T − i) + ε(T ). (5)
Since (N
0
a
N
T
), we use low values of p, i.e., p =
1, 2, 3. Hence, we use VAR(1), VAR(2), and VAR(3)
models for our case study. Determining the optimal
choice of p values using the minimization of statistics
such as Akaike (AIC), Schwarz-Bayesian (BIC), etc.
is in the scope of future work.
Using both AR and moving-average (MA) models
together addresses a generalized structure. If we treat
the N
0
a
attributes independently, then we can use each
of their time series in an ARMA model for predictive
analysis. An ARMA(p,q) process has two parameters
– p is the order of the autoregressive model, and q is
the order of the MA, i.e, moving average part), which
gives the number of error terms considered. For time
series (scalar) values y at time instance T , constant
value c, coefficients of AR model ϕ, coefficients of
MA model θ, and error term ε(T ),
y(T ) = c +
p
∑
i=1
ϕ
i
y(T − i) +
q
∑
i=1
θ
i
ε(T − i). (6)
Since (N
0
a
N
T
), we use low values of q also. Thus,
in our case study, we use p = 1, 2, 3 and q = 1, 2
in an ARMA(p,q) process. Thus, we implement six
ARMA(p,q) models with the selected (p, q).
Using the predicted values of the elements of the
reduced PCAM, P
0
, we reconstruct the matrix. The
complete step-by-step procedure of CAP-DSDN is as
given in Algorithm 1.
4.4 Prediction Evaluation
Given the absence of ground truth, we use the time se-
ries data for (N
T
−3) time instances for our analysis to
predict the remaining three time instances. Currently,
the value of three is conservatively chosen to indicate
short-term prediction and assuming that most of the
DSDNs have more than three snapshots.
We compare our predicted co-association values
with those values computed directly from the data
of these time instances for validation. For compari-
son, we use the metrics conventionally used in clus-
tering algorithms, especially in the absence of ground
truth. We use the Normalized Mutual Information
Score (NMI) (Studholme et al., 1998) and Rand In-
dex (RI) (Rand, 1971) here.
NMI is a measure of the similarity between two
label assignments of the same data, indicating mutual
agreement of labels between the assignments. NMI
values range from 0 to 1, implying the strength of
the agreement. While the bounded values of NMI are
an advantage for comparisons, NMI not adjusting for
chance is a disadvantage for our case study. For two
label assignments, U and V , with L and M classes,
respectively, mutual information (MI) and NMI are
computed, for N objects using entropy measure H, as:
H(U) =
|L|
∑
i=1
P(i)log(P(i));
H(V ) =
|M|
∑
i=1
P
0
( j)log(P
0
( j)),
where the probabilities P(i) and P
0
( j) are computed
using the number of instances in U and V in the i
th
and j
th
classes, respectively.
Thus, P(i) =
|Class(i)|
N
and P
0
( j) =
|Class( j)|
N
.
When comparing the two labeling assignments, there
may be some instances with both labels i and j. Thus,
the joint probability is:
P(i, j) =
|Class(i)∩|Class( j)|
N
.
Thus, MI(U,V ) =
|L|
∑
i=1
|M|
∑
j=1
P(i, j). log
P(i, j)
P(i).P
0
( j)
.
We normalize using the sum, i.e., the mean, as it is
considered a good trade-off when considering mini-
mum, mean, and maximum value as the normalizing
factor (Kvalseth, 1987). Thus, the normalized value
NMI(U,V ) =
MI(U,V )
mean(H(U),H(V))
.
We consider 0 and 1 in the (binarized) CAM as labels,
thus, giving |L| = |M| = 2.
RI is another similarity measure between the ac-
tual community distribution and the predicted com-
munity distribution by considering all pairs of objects,
and by counting the pairs that are assigned in the same
or different clusters in the predicted and true cluster-
ings. RI is the ratio of the number of common pairs
CAP-DSDN: Node Co-association Prediction in Communities in Dynamic Sparse Directed Networks and a Case Study of Migration Flow
69

to the total number of pairs. We use the unadjusted
RI, bounded in [0,1], as it provides the accuracy of
element pair labeling as given by the clustering.
4.5 Implementation
We have used Python for implementing our proposed
work. CDlib (Rossetti et al., 2019) has been used
for community detection algorithms and metrics. The
time series regression models VAR and ARMA have
been implemented using statsmodels (Seabold and
Perktold, 2010). The validation for prediction using
the metrics for clustering has been implemented us-
ing scikit-learn (Pedregosa et al., 2011). Shannon
entropy has been computed using scipy.stats (Vir-
tanen et al., 2020), using the default logarithm base e,
i.e., natural logarithm.
5 CASE STUDY: EXPERIMENTS
& RESULTS
In this section, we present the results of CAP-
DSDN (Figure 1) on a case study of international
refugee migration over an extended period.
International Refugee Migration Flow: We ana-
lyze the DSDN in a specific case study of inter-
national refugee migration flow between countries.
The dataset, obtained from the United Nations Hu-
man Rights Commissioner (UNHCR)
2
.This publicly
available dataset has year-wise records of migrant
count from origin to destination (or asylum) coun-
tries, which are the flow values. While the refugee
data in the UNHCR database is available from the
year 1951, the count of asylum seekers was first avail-
able in 2000. Hence, we use the annual data starting in
2000 and thus, focus on the time period during 2000-
2018. In this time period, there are 208 countries of
origin and 186 countries of asylum. After pruning
nodes that have only zero-weighted edges for all the
snapshots, we reduce the node-set to 190 countries.
Thus, our DSDN has 190 nodes for 19 snapshots.
Given the absence of ground truth, we use 2000-
2015 data to predict the PCAM for 2016-2018 of the
significant subnetwork, and the predicted values are
compared against the computed values from the orig-
inal data for validation.
Selection of CD Algorithm: The evaluation results
of the three selected community detection algorithms
are reported in Table 1 for a representative year, 2018,
2
Dataset: https://www.unhcr.org/refugee-statistics/
download/
which is the last year. For the link (LM) modular-
ity, SLPA and MODN show more similar values and
IMAP has a relatively lower value. For Z-Modularity
(ZM), MODN performs better than IMAP and SLPA.
The modularity values closer to zero indicate a sin-
gle large community (Fortunato, 2010), and higher
positive values, but less than one, indicate better par-
titioning. The LM values for the three algorithms
may be explained by the community characteristics
in the year 2018 (Figure 2, (i)-(ii)). We observe
that SLPA gives the highest count of communities
whereas IMAP gives the lowest, but all three gives
similarly sized largest community. Thus we observe
that IMAP has the lowest variation in community
sizes, and SLPA tends to have several smaller com-
munities, indicating a higher degree of fragmentation.
Since ZM is designed to address the issue of reso-
lution limit, we observe that MODN with a consider-
able number of communities, and with moderate vari-
ation in community sizes, performs well. The com-
munity characteristics in Figure 2 also explain the rel-
atively high values of IMAP for Internal Edge Den-
sity (IED), Average Internal Degree (AID), and Cut
Ratio (CR) metrics, indicating the best performance
by IMAP. Higher values of these metrics imply better
communities. SLPA has a distinct advantage in the
case of networks with overlapping communities (Xie
et al., 2011). We observe that SLPA does not per-
form as well as IMAP and MODN, with respect to
our chosen metrics, as our case study does not have
any relevance for overlapping communities.
Overall, we observe from Table 1 that there is
no single CD algorithm that distinctively or consis-
tently performs the best, with respect to our chosen
metrics. This can be explained by the known obser-
vation that these CD algorithms detect a large num-
ber of small and connected whisker-like communities
and a large core with several intermingled communi-
ties. Using the community structure characteristics
shown in Figure 2 (i)-(ii), we conclude that IMAP
performs the best as it demonstrates the community
structure with a large core (Figure 2 (ii)). Thus, IMAP
is an appropriate choice for community detection and
prediction of international refugee migration flow in
our case study, as demonstrated in (Table 1 and Fig-
ure 2). It must be noted that algorithms that disregard
the edge directionality information, e.g., MODN, are
not considered to be accurate (Agreste et al., 2016).
Hence, even though MODN gives a moderate per-
formance, we have disregarded MODN here. With
respect to time complexity, SLPA is the fastest, fol-
lowed by IMAP closely, but MODN has the worst
performance (Agreste et al., 2016). Since time com-
plexity is also a critical factor for the choice of CD
KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval
70
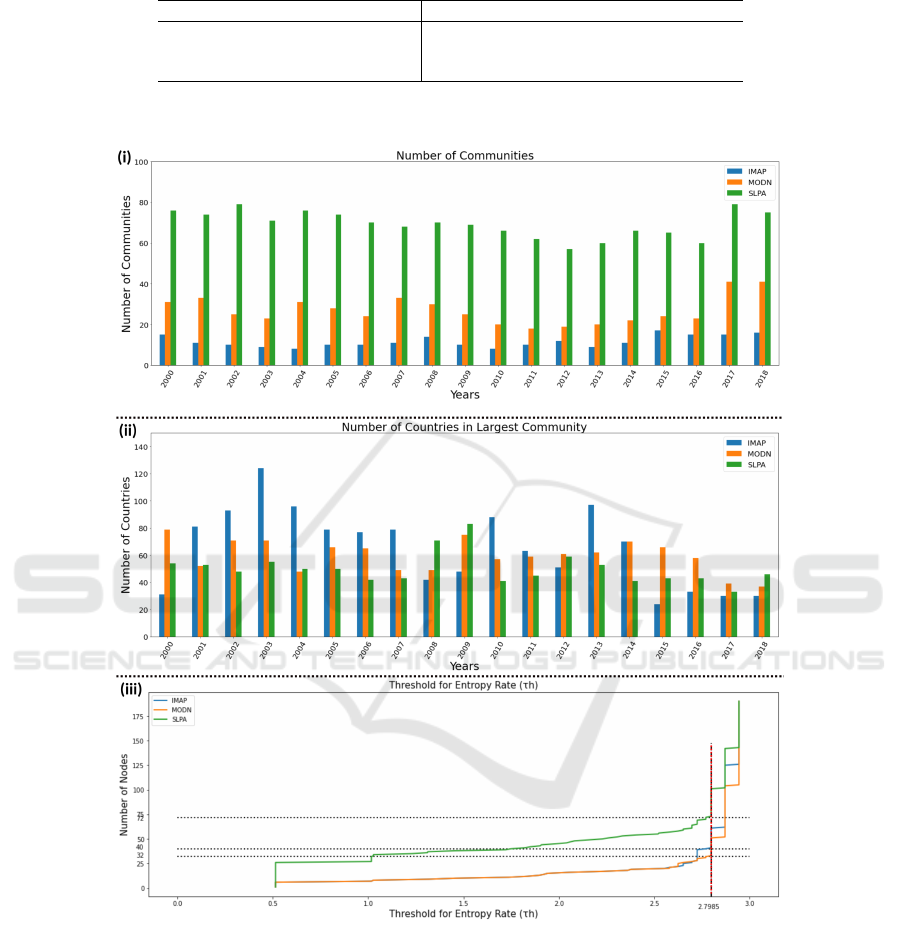
Table 1: Comparing communities in the international refugee migration flow in the year 2018, in 190 countries, using different
algorithms, evaluated by different metrics.
Community Detection Algorithm LM IED AID CR ZM
SLPA 0.028 0.019 0.643 0.004 0.108
MODN 0.028 0.009 1.093 0.005 0.451
IMAP 0.019 0.114 3.647 0.048 0.207
SLPA: speaker-listener label propagation algorithm; MODN: modularity optimization in a directed network; IMAP: Infomap algorithm.
LM: link modularity; IED: internal edge density; AID: average internal degree; CR: cut ratio; ERM: Erd
¨
os-R
´
enyi modularity; ZM: Z-modularity.
Figure 2: For the selected CD algorithms, (i)-(ii) characteristics of CD outcomes, and (iii) number of nodes retained for
different thresholds for determining entropy rate τ
h
(red dotted line), for the international refugee migration flow in 190
countries (nodes of the DSDN).
algorithm, IMAP is the optimal choice here.
Node-filtering the Network: Each CD algorithm can
independently have its own τ
h
. But, in this case study,
we observe that all three algorithms have the same
τ
h
= 2.799 as the transition point for entropy rate in
their CD outcomes (Figure 2, (iii)). Using this value
as the threshold, we get node-filtered networks of size
n
0
, i.e., 72, 32, and 40 nodes, in the case of SLPA,
MODN, and IMAP, respectively. This indicates that
IMAP is a conservative choice.
Time Series Modeling and Prediction: A summary
of the experiments for the IMAP algorithm (for both,
VAR and ARMA) for the network sizes upon filter-
ing, are given in Table 2. For each VAR experiment,
CAP-DSDN: Node Co-association Prediction in Communities in Dynamic Sparse Directed Networks and a Case Study of Migration Flow
71
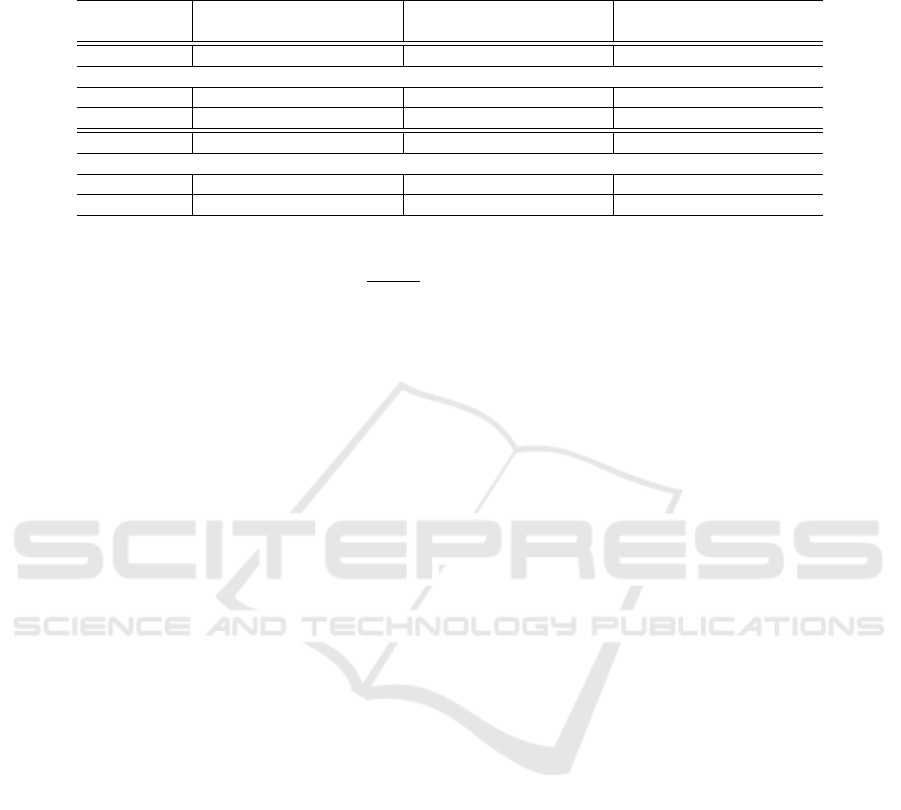
Table 2: Comparison of the predicted PCAMs using autoregressive models, i.e., VAR(p) and ARMA(p,1) models, for com-
munities detected using Infomap algorithm (IMAP), in the international refugee migration network with n = 190 nodes, giving
n
0
nodes after node-filtering the DSDN using threshold τ
h
, in different prediction years (Pred. Yr.).
Pred. Yr. → 2016 2017 2018
Metric ↓
VAR(p) p = 1 p = 2 p = 3 p = 1 p = 2 p = 3 p = 1 p = 2 p = 3
τ
h
= 2.799, n
0
= 40, Using IMAP
NMI 0.000 0.000 0.064 0.000 0.000 0.000 0.000 0.000 0.000
Rand-Index 0.943 0.943 0.945 0.982 0.982 0.980 0.992 0.992 0.990
ARMA(p,1) p = 1, p = 2, p = 3, p = 1, p = 2, p = 3, p = 1, p = 2, p = 3,
τ
h
= 2.799, n
0
= 40, Using IMAP
NMI 0.039 0.039 0.039 0.015 0.015 0.015 0.008 0.008 0.008
Rand-Index 0.057 0.057 0.057 0.018 0.018 0.018 0.008 0.008 0.008
NMI: normalized mutual information; VAR: vector auto-regression; ARMA: auto-regressive moving average.
the time series of the vector v of size N
0
a
=
n
0
(n
0
−1)
2
,
as the vector is obtained from the half vectorization
of the reduced PCAM (of n
0
nodes), after discarding
the zeros on the diagonal. On the other hand, ARMA
is implemented separately for the time series of N
0
a
different elements of v, used in the VAR model. We
make three major observations.
Firstly, the RI gives more variation in the results
than the NMI values, as the latter is a more stringent
validation metric than the former. This is because RI
compares pairwise similarities in the binary values in
the predicted and the original CAMs, whereas NMI
directly compares the matrix values in the CAMs.
Secondly, the VAR model gives better results
than the ARMA model, which can be explained by
the consideration of interdependence between the at-
tributes in the former than in the latter. Also, the dis-
parity N
0
a
N
T
, for N
T
time instances, plays a role in
over-fitting solutions for the ARMA model.
Thirdly, the AR parameter p value does not have
any impact on improving the ARMA model. p = 1, 2
show best results for the VAR(p) model. Given the
disparity, p = 1 may be considered the most conserva-
tive value for the VAR(p). We also found that the MA
parameter q = 2 showed the same results as q = 1,
in the ARMA(p,q) model. Hence, we consider only
AR(p,q) only for q = 1 in our experiments.
Overall, IMAP gives the best result for VAR(1)
for the year 2018. Given the political volatility of in-
ternational refugee migration, short-term predictions
are preferred over long-term ones. Thus, we conclude
that CAP-DSDN can be effectively used in interna-
tional refugee migration flow analysis for conserva-
tive predictions of the community structure in the sig-
nificant subnetwork over three years.
As an example of co-association available from
the dataset, the communities in the network in the
year 2015 show that the USA and Mexico are in
the same community. Based on the trend of the re-
duced number of migrations due to geopolitical cir-
cumstances over the years, our model predicts their
co-association to be zero in 2018. The actual co-
association value matches the same and correlates
with the fact that the proportion of the Mexican-born
population in the USA declined from 28% to 26% in
this duration (Krogstad and Radford, 2017).
Another example is that of Australia, where the
migration rates have continued to decline since 2004.
The CAM in 2015 shows that Australia belongs to
a community of 65 countries. The predicted CAM
shows that the community behavior has fallen steeply,
and Australia belongs to a community with 37 coun-
tries, which is reasonably close to the actual value of
29 (United Nations, Dept. of Econ. & Soc. Affairs,
Population Div., 2015).
6 CONCLUSIONS
It is important to note that in the previous litera-
ture while determining communities in DSDNs, the
community of nodes is seen as an entity rather than
its pairwise relationships. Instead of performing a
time series analysis of the network itself or its com-
munities, we have shifted our focus to the inter-
relationships between the network nodes which is
a novelty of CAP-DSDN. In this node-centric ap-
proach, we use the relationship of co-association in a
community, which we use for predictive analysis. We
use the co-association matrices (CAM) to represent
these relationships while representing the discovered
communities of nodes indirectly. When using a time
window, the moving average smoothing of the CAM
gives a likelihood value for the co-association rela-
tionship, which is the PCAM. Furthermore, we use
the elements of PCAM as attributes for the predictive
model for a time series dataset. Lastly, the outcome of
our study is in predicting the co-association value at a
KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval
72

future date, thus indirectly predicting the community
structure in a significant subnetwork. This significant
subnetwork retains only the nodes with a strong com-
munity forming tendency over time, determined using
our novel entropy rate metric. Overall, our results in
the case study of the international refugee migration
network demonstrate that the effectiveness of our pro-
posed method depends strongly on the completeness
of the time series data.
There are limitations in our work stemming from
the data quality and availability, concerning the mi-
gration flow datasets. Finding datasets outside of mi-
gration flow is non-trivial, given the nuanced proper-
ties expected of the dataset, i.e., directed networks,
sparse, and with time series. Further research can be
pursued for migration flow data analysis itself in im-
proving the data quality using imputation and other
methods appropriate for the data.
ACKNOWLEDGEMENTS
The authors acknowledge the support of the IIIT Ban-
galore and the IIT Kharagpur summer internship pro-
gram for conducting this work. The authors are
grateful to the anonymous reviewers whose sugges-
tions have improved this paper. This publication
is supported by the grant by the Science and Engi-
neering Research Board (SERB), Government of In-
dia, under the Mathematical Research Impact Sup-
port (MATRICS). The authors are thankful to the help
provided by members of the Graphics-Visualization-
Computing Lab.
REFERENCES
Agreste, S., De Meo, P., Fiumara, G., and et al. (2016).
An empirical comparison of algorithms to find com-
munities in directed graphs and their application in
web data analytics. IEEE Transactions on Big Data,
3(3):289–306.
Bongiorno, C., Zino, L., and Rizzo, A. (2019). A novel
framework for community modeling and characteri-
zation in directed temporal networks. Appl. Net. Sc.,
4(1):1–25.
Box, G. and Jenkins, G. (1970). Time Series Analysis: Fore-
casting and Control. Holden-Day, San Francisco.
Cai, D., Campbell, T., and Broderick, T. (2016). Edge-
exchangeable graphs and sparsity. Advances in Neural
Info. Processing Sys., 29.
Cover, T. M. and Thomas, J. A. (2006). Elements of Infor-
mation Theory (Wiley Series in Telecommunications
and Signal Processing). Wiley-Intersc.
Fortunato, S. (2010). Community Detection in Graphs.
Phys. Reports, 486(3-5):75–174.
Krogstad, J. M. and Radford, J. (2017). Key facts about
refugees to the US. Pew Rsrch. Cntr., 30.
Krzakala, F., Moore, C., Mossel, E., Neeman, J., Sly, A.,
Zdeborov
´
a, L., and Zhang, P. (2013). Spectral re-
demption in clustering sparse networks. Proceedings
of the National Academy of Sciences, 110(52):20935–
20940.
Kvalseth, T. O. (1987). Entropy and correlation: Some
comments. IEEE Transactions on Systems, Man, and
Cybernetics, 17(3):517–519.
Leicht, E. A. and Newman, M. E. (2008). Community
structure in directed networks. Phys. Rev. Letters,
100(11):118703.
Malliaros, F. D. and Vazirgiannis, M. (2013). Clustering and
community detection in directed networks: A survey.
Phys. Reports, 533(4):95–142.
Martin, S., Mor
˘
arescu, I.-C., and Ne
ˇ
si
´
c, D. (2016). Time
scale modeling for consensus in sparse directed net-
works with time-varying topologies. In 2016 IEEE
55th Conference on Decision and Control (CDC),
pages 7–12. IEEE.
Mirshahvalad, A., Lindholm, J., Derlen, M., and Rosvall,
M. (2012). Significant communities in large sparse
networks. PloS one, 7(3):e33721.
Miyauchi, A. and Kawase, Y. (2016). Z-score-based modu-
larity for community detection in networks. PloS one,
11(1):e0147805.
Neumayer, E. (2005). Bogus refugees? The determinants
of asylum migration to Western Europe. International
studies quarterly, 49(3):389–409.
Nicosia, V., Mangioni, G., Carchiolo, V., and Malgeri,
M. (2009). Extending the definition of modular-
ity to directed graphs with overlapping communi-
ties. Jrnl. of Stat. Mech.: Theory and Experiment,
2009(03):P03024.
Pedregosa, F., Varoquaux, G., Gramfort, A., and et al.
(2011). Scikit-learn: Machine Learning in Python.
Journal of Machine Learning Research, 12:2825–
2830.
Pons, P. and Latapy, M. (2006). Computing communities in
large networks using random walks. Journal of Graph
Algorithms and Applications, 10(2):191–218.
Radicchi, F., Castellano, C., Cecconi, F., Loreto, V., and
Parisi, D. (2004). Defining and identifying communi-
ties in networks. PNAS, 101(9):2658–2663.
Rand, W. M. (1971). Objective criteria for the evaluation of
clustering methods. Journal of the American Statisti-
cal Association, 66(336):846–850.
Rossetti, G. and Cazabet, R. (2018). Community discov-
ery in dynamic networks: A survey. ACM Computing
Surveys (CSUR), 51(2):1–37.
Rossetti, G., Milli, L., and Cazabet, R. (2019). CDLIB:
A Python Library to Extract, Compare and Evaluate
Communities from Complex Networks. Applied Net-
work Science, 4(1):1–26.
Rosvall, M. and Bergstrom, C. T. (2008). Maps of random
walks on complex networks reveal community struc-
ture. PNAS, 105(4):1118–1123.
CAP-DSDN: Node Co-association Prediction in Communities in Dynamic Sparse Directed Networks and a Case Study of Migration Flow
73

Seabold, S. and Perktold, J. (2010). statsmodels: Econo-
metric and statistical modeling with Python. In 9th
Python in Science Conference.
Sims, C. A. (1980). Macroeconomics and reality. Econo-
metrica: journal of the Econometric Society, pages
1–48.
Singh, A. and Humphries, M. D. (2015). Finding commu-
nities in sparse networks. Scientific reports, 5(1):1–7.
Stein, S. and Leng, C. (2021). A Sparse Random Graph
Model for Sparse Directed Networks. arXiv preprint
arXiv:2108.09504.
Studholme, C., Hawkes, D. J., and Hill, D. L. G. (1998).
Normalized entropy measure for multimodality image
alignment. In Medical Imaging 1998: Image Process-
ing, volume 3338, pages 132–143. Intl. Society for
Optics & Photonics.
Suleimenova, D., Bell, D., and Groen, D. (2017). A general-
ized simulation development approach for predicting
refugee destinations. Scientific reports, 7(1):1–13.
United Nations, Dept. of Econ. & Soc. Affairs, Population
Div. (2015). International Migration Flows to and
from Selected Countries: The 2015 Revision.
Virtanen, P., Gommers, R., Oliphant, T. E., et al., and SciPy
1.0 Contributors (2020). SciPy 1.0: Fundamental Al-
gorithms for Scientific Computing in Python. Nature
Methods, 17:261–272.
Wang, B., Gao, L., and Gao, Y. (2012). Control range: a
controllability-based index for node significance in di-
rected networks. Jrnl. of Stat. Mech.: Theory and Ex-
periment, 2012(04):P04011.
Xie, J., Szymanski, B. K., and Liu, X. (2011). SLPA: Un-
covering overlapping communities in social networks
via a speaker-listener interaction dynamic process. In
IEEE 11th Intl. Conf. on Data Mining Workshops,
pages 344–349. IEEE.
KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval
74
