
Improving Digital Circuit Synthesis of Complex Functions using Binary
Weighted Fitness and Variable Mutation Rate in Cartesian Genetic
Programming
Prashanth H. C.
a
and Madhav Rao
b
International Institute of Information Technology Bangalore, India
Keywords:
CGP, Evolutionary Algorithms, Non-linear Functions, Digital Circuit Synthesis.
Abstract:
Cartesian Genetic Programming (CGP) is regularly applied to synthesize and realize digital circuits for small
arithmetic and digital-logic functions. CGP benefits in obtaining hardware-efficient circuits through its heuris-
tic search-space exploration, which is hard to reach in a rule-based synthesis process. However, the traditional
CGP configuration has limitations in evolving large and complex circuits, requiring a large number of gen-
erations. High computation time and energy requirements hinder its usage from evolving complex digital
circuits. This paper investigates and demonstrates the desired modifications to existing CGP in the form of
Binary Weighted Fitness (BwF) and exponentially varying mutation rate (eVar) to evolve functionally correct
solutions extremely fast. The benefits are demonstrated for the basic non-linear power functions and are vali-
dated for usage in activation functions which are otherwise difficult to realize. Additionally, 12 different CGP
configurations with changes in mutation scheme and evolutionary strategy were also investigated for the power
functions. A comparison with the benefits of BwF and eVar adopted CGP over the traditional CGP methods
is presented and discussed.
1 INTRODUCTION
The ultimate goal of logic synthesis process is to build
optimized version of gate-level designs with mini-
mum number of cells and logic depth, which directly
benefits the circuit’s performance on silicon (Berndt
et al., 2021; Kocnova and Vasicek, 2020). The cur-
rent ABC synthesis tool (Brayton and Mishchenko,
2010) employs directed acyclic graphs to represent
circuits. The graph is structured around two-input
AND nodes and their associated edges, which are
referred to as AND-Inverter Graph (AIG). The opti-
mization involves minimizing AIG size by iteratively
replacing the subgraphs with pre-computed ones, but
retaining the node functionality (Mishchenko et al.,
2006). Although simple and scalable, this synthe-
sis method fails to represent XOR and XNOR gates
with less than 3 AIG nodes each. Hence the current
synthesis method is not considered robust enough to
represent real-world designs which are generally non-
linear in nature (Fi
ˇ
ser et al., 2010; Sekanina et al.,
2014).
a
https://orcid.org/0000-0002-9650-3731
b
https://orcid.org/0000-0003-2278-9148
Evolutionary algorithms involving cartesian ge-
netic programming (CGP) are adopted to synthesize
circuits, especially for the ones that are hard to real-
ize (Sekanina et al., 2014; Prashanth and Rao, 2022;
Miller and Harding, 2008). However, with the grow-
ing complexity of the co-processor design require-
ments, the evolutionary approach tends to either fail
for gate count above 10K or concedes exorbitant time
to realize the gate level circuits (Vasicek, 2015). An
advanced method in the form of a cut-based method
for evolutionary synthesis was proposed in (Vasicek,
2015), offering less number of gate designs but at
the cost of slower convergence. A boolean network
scoping driven re-synthesis approach was attempted
where the CGP was applied on the extracted sub-
circuits, and placed back to the original circuit with
an intention of global level optimization. The sub-
circuits picked for CGP driven re-synthesis either
concedes time if the size is large, or does not of-
fer much benefits at global level if the size of the
sub-circuit is small. To overcome this problem a
cut-based method for evolutionary synthesis was pro-
posed in (Vasicek, 2015) offering less number of
gates design, but at the cost of slower convergence.
A search-based strategy to optimize and approximate
112
H. C., P. and Rao, M.
Improving Digital Circuit Synthesis of Complex Functions using Binary Weighted Fitness and Variable Mutation Rate in Cartesian Genetic Programming.
DOI: 10.5220/0011539000003332
In Proceedings of the 14th International Joint Conference on Computational Intelligence (IJCCI 2022), pages 112-120
ISBN: 978-989-758-611-8; ISSN: 2184-3236
Copyright © 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

a sub-circuit towards FPGA system design was pre-
sented in (Vasicek and Sekanina, 2016) that adopted
CGP to re-synthesize the circuit. Overall, CGP of-
fered better trade-off metrics between hardware de-
sign parameters and error metrics when compared
with other traditional practices (Miller and Harding,
2008). However, the runtime incurred to synthe-
size circuits is extremely high, especially for a higher
number of inputs and for complex non-linear func-
tionalities (Hodan et al., 2020). Moreover, due to the
surge in the applied machine-learning, and artificial
intelligence techniques, higher-order computations in
the order of 32-bits or 64-bits data-format are man-
dated (Miyasaka et al., 2021). Evolving hardware
designs for designs with large number of input re-
quire faster genetic programming algorithms, without
compromising on the fitness achieved. On the con-
trary, higher-order functional design is likely to im-
pose tight constraints on the fitness, since a minute
deviation is expected to induce large errors in the pro-
cessed data. Hence, there is a timely need for running
CGP and arriving at the solution much faster without
compromising on the fitness.
Sections 2 and 3 describe related work and CGP
configurations. In section 4 we introduce the pro-
posed modifications to CGP, and section 5 analyse the
impact on basic non-linear functions. Section 6 show-
cases the advantage of modifications when used in the
synthesis of activation functions in Neural Networks.
2 RELATED WORK
CGP and its variants were explored and thoroughly
investigated in the past (Miller, 2020; Manazir and
Raza, 2019). To briefly summarize, the CGP vari-
ants in the form of graph-based crossover and applied
mutation operators were discussed in (Miller, 2020).
However, multiple mutations invariably run on mul-
tiple threads or processes till functional crossover is
attained, which indirectly consumes more computa-
tional resources to allow for context switching be-
tween the multiple processes. The only possible ad-
vantage is attaining a quick graphical crossover, de-
pendent on the initial seeding and highly correlated
mutation operators. Modular CGP is another ex-
tended version of the original, where additional mu-
tation operators allow CGP-encoded sub-functions to
be re-evaluated and re-synthesized. However, evolv-
ing to a sub-functional genotype first-up is a com-
putationally heavy task. Furthermore, evolved sub-
functions may not necessarily converge to an opti-
mized solution and a slight deviation in the generated
sub-functions may lead to functionally incorrect de-
signs. A different method of taking CGP phenotype
to machine code for faster execution was attempted.
A whole set of implementations with a speedup in
the CGP run was achieved by executing the runs on
the hardware units such as FPGAs, and application-
specific virtual reconfigurable circuit (VRC) (Va
ˇ
s
´
ı
ˇ
cek
and Sekanina, 2012; Hrb
´
a
ˇ
cek and Drahosova, 2013),
which are categorically, a different set of approaches.
Overall, most modifications aim to add more opera-
tive dimensions or shift the execution to a completely
different platform to improve the operational speed.
The current CGP methods exploited in the literature
do not address any speedup mechanism to arrive at
fitter solutions. This paper proposes two new modi-
fications to the existing CGP methodology to achieve
the desired synthesized gate-level circuits with lesser
generations and, at the same time, extract a group of
fitter solutions. The two mechanism includes:
1. Applying a different mutation rate, siilar to
(Thierens, 2002). Especially for realizing non-
linear functions instead of a constant mutation rate
adopted in the traditional methods, and
2. Incorporating a binary-weighted fitness function
instead of the same weight across the data-format
of the functions under synthesis.
The proposed modifications to the CGP run are highly
useful for realizing hardware designs for non-linear
functions, which are essential components of the
modern-day neural network and its family of compu-
tational networks. Hardware realization of two types
of non-linear functions is demonstrated to showcase
the impact of the proposed CGP method - i) Power
functions and ii) Activation functions. The paper con-
tributes to introducing an exponential mutation rate
(eVar) and binary-weighted fitness function (BwF)
for synthesizing non-linear functions. As per the au-
thors’ knowledge, this is the first time a varying muta-
tion rate and binary-weighted fitness across the data-
format is adopted and analysed for circuit synthesis.
3 CARTESIAN GENETIC
PROGRAMMING
In CGP, a directed acrylic graph (DAG) consisting
of an array of gates is evolved iteratively for the de-
sired function (Miller and Harding, 2008). Nodes of
the DAG are gates picked from the predefined list
employed to build the combinational circuit. The
DAG, which is defined using encoded genotype, is
mutated repeatedly in an attempt to obtain the cor-
responding phenotype (digital circuits) that performs
better in the desired objective functions. Objective
Improving Digital Circuit Synthesis of Complex Functions using Binary Weighted Fitness and Variable Mutation Rate in Cartesian Genetic
Programming
113
f
i
0
i
r-1
f
i
0
i
r-1
f
i
0
i
r-1
f
i
0
i
r-1
f
i
0
i
r-1
f
i
0
i
r-1
f
i
0
i
r-1
f
i
0
i
r-1
f
i
0
i
r-1
0
1
n-1
n
n+1
m.n-1
2n-1
n.(m-1)
n.(m-1)+1
I
0
I
1
I
2
I
k
O
0
O
1
O
j
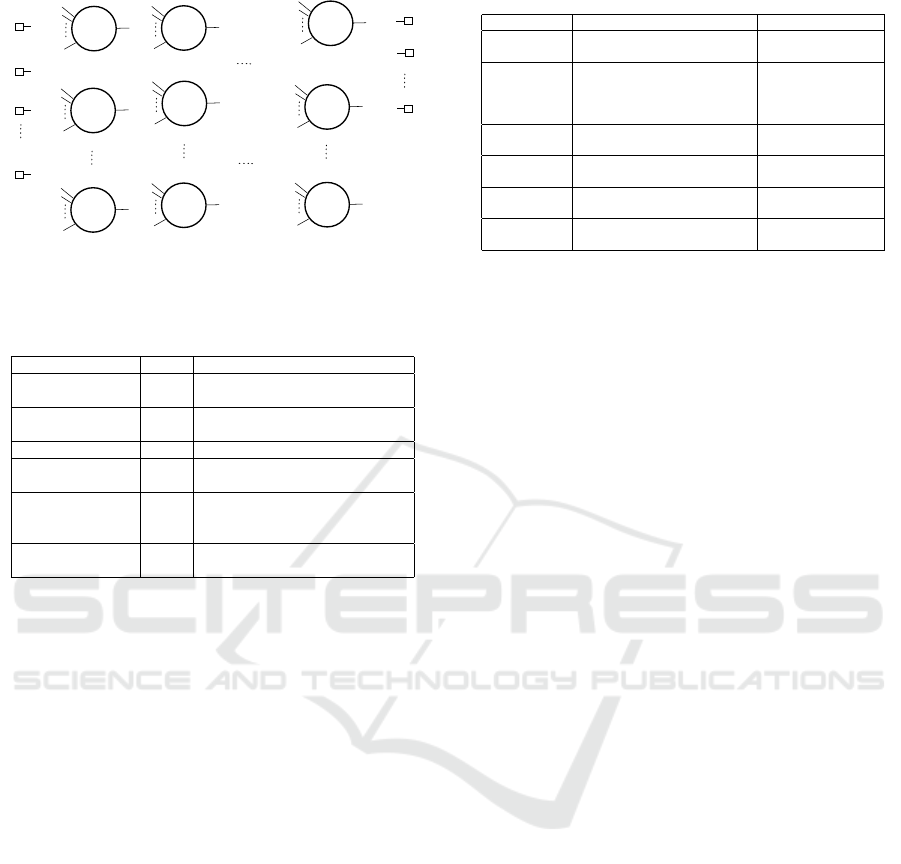
Figure 1: A schematic representation of Cartesian Genetic
Programming (CGP) showing 2D DAG for inputs I, gener-
ating outputs O.
Table 1: CGP Parameters.
Parameter Value Description
No. of Generations G > 0
The maximum no. of generations
in a evolutionary run
Nodes (n) n > 0
Number of usable nodes
for the algorithm
Arity A > 0 Arity of each node
Function Set
Available functions to be used
as nodes
Mu µ > 0
No. of Parents passed to the
next generation, also used to create
children
Lambda λ > 0
No. of children created using µ
parents
functions can be functional correctness of the circuit,
hardware performance metrics (area, delay or power
of the circuit) or a multi-objective function combin-
ing both functional correctness and hardware metrics.
Figure 1 shows a general node-level representation
of CGP DAG, where each node represents a func-
tional block. For n rows and m columns, each node
is a functional gate selected from a predefined set of
f ∈ F. The arity r defines the number of inputs for
each node. In this work, the function set F is a com-
bination of basic standard two-input gates consisting
of 2-NAND, 2-OR, 2-NOR, 2-OR, 2-XOR, 2-XNOR.
The parameters listed in Table 1 are utilized to con-
figure the CGP algorithm for synthesis. Algorithm 1
presents the (µ+λ) evolutionary strategy steps, which
returns the fittest genotype in an algorithm run with
randomly generated seed candidate solutions. The µ
value indicates the number of solutions promoted to
the next generation as parents. The λ value indicates
the number of off-springs generated from the µ par-
ents from the previous generation. In this work, dif-
ferent evolutionary strategies were also analyzed to
identify the ideal µ, λ values for achieving faster evo-
lution of non-linear digital circuits. To showcase the
impact of a novel mutation rate and modified fitness
function, non-linear activation functions and power
functions were realized using the modified features of
the CGP technique. The original CGP with constant
Table 2: CGP Configurations.
Configuration Possible choices Typical Choice
Evolutionary
Strategy
(µ + λ) (1 + 4)
Mutation
Scheme
Probabilistic,
Probabilistic Only Active,
Point,
Single
Point
Selection
Scheme
Select Fittest,
Tournament
Select Fittest
Reproduction
scheme
Mutate every parent,
Mutate random parent
Mutate Every Parent
Fitness
Supervised Learning (SL),
Binary weighted Fitness (BwF)
Supervised Learning
Mutation
Rate
Constant,
Variable
Constant
mutation rate and traditional fitness function for all
the non-linear functions were also evaluated and com-
pared against the proposed modified CGP techniques.
All possible options and typically selected configura-
tions are listed in Table 2. The four mutation schemes
vary in terms of the mutations performed on node and
chromosome level. The mutation schemes are elabo-
rated below.
Probabilistic : Conducts probabilistic mutation on
the given chromosome. Each chromosome gene is
changed to a random valid allele with a specified
probability.
Probabilistic Only Active : Conducts probabilistic
mutation on the active nodes in the given chro-
mosome. Each chromosome gene is changed to a
random valid allele with a specified probability.
Point : Conducts point mutation on the given chro-
mosome. A predetermined number of chromo-
some genes are randomly selected and changed to
a random valid allele. The number of mutations is
the number of chromosome genes multiplied by
the mutation rate. Each gene has equal probabil-
ity of being selected.
Single : Conducts a single active mutation on the
given chromosome.
Although the paper emphasizes novel fitness func-
tion (BwF) and varying mutation rate (eVar), the other
configurations, including evolutionary strategy, mu-
tation scheme, selection scheme, and reproduction
schemes were also investigated for the synthesis runs.
Select Fittest selection scheme and Mutate Every Par-
ent reproduction scheme was incorporated for all the
evolutionary runs. As indicated in Table 2, typical
CGP in the form of Supervised learning (SL), Con-
stant mutation rates were compared against BwF, and
variable mutation rate CGP technique towards synthe-
sizing digital circuits of non-linear functions.
ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications
114

Algorithm 1: (µ + λ) evolutionary strategy.
forall i such that 0 ≤ i < (λ + 1) do
Randomly generate individual i
end
Select µ individuals, that are promoted as the
parents.
while the generation limit is not reached do
forall i such that 0 ≤ i < λ do
Mutate the µ parents based on the
mutation scheme to generate λ
offsprings
end
Generate the fittest individual using the
following rules:
if an offspring genotype ranks better in a
selection scheme then
Offspring genotype is chosen as fittest
else
The parent chromosome remains the
fittest
end
end
4 PROPOSED DESIGN
4.1 eVar
In traditional CGP, the mutation rate is configured
to be a constant value in a view to have the same
mutation rate across the generations and continue to
evolve until a desired fitness or termination crite-
ria is achieved (Miller and Harding, 2008). In this
work, we intend to formulate a mechanism that intu-
itively selects between rough topologies in the initial
generations and then mutates sub-parts of the best-
performing circuit topologies—followed by minimal
and single gate level selection in the final generations.
This mechanism is inspired by varying learning rate in
various ML optimization algorithms during the train-
ing phase. The fitness function used can achieve the
selection between the rough topologies in the initial
generations and subsequently among the finer sub-
parts of the designs in the later runs. We tried sev-
eral types of mutation rate variations, including linear
and various non-linear decays. It is observed that an
exponential variation of the mutation rate converges
fastest to functionally correct circuits.
mutation rate(g) = R × e
−g
0.1×G
,
(1)
where,
G = Total number of generations,
g = current generation, and
R = initial rate of mutation.
Exponential variation of mutation rate used is
stated in Equation 1. It is observed that a decay
rate of 10 is apt based on our heuristic studies on
evolving non-linear functions. If the mutation rate re-
duces lower than one gene, the mutation scheme was
changed to mutate at least one gene for further gen-
erations to continue the evolution process. The se-
quence of a first-up rough design requires high muta-
tions to evolve to a relatively adequate design topol-
ogy. Further fine-tuning the design topology with
fewer mutations requires lower mutation rates. The
process of following exponentially varying mutation
rates was found to inherently reduce the evolution
time to achieve similar fitness as other variations. The
selection between multiple mutated designs at all gen-
erations is driven by the configured fitness function.
4.2 BwF
Binary weighted fitness (BwF) was introduced to
evolve designs which are closer to the data-formatted
functional output. The traditional SL (Supervised
Learning) fitness can either be devised to formulate a
minimizing or maximizing objective function for the
evolutionary algorithm. For the minimizing case, SL
uses Hamming distance between the evolved circuit
output data-bits and expected output data-bits over all
input combinations, indicating the total number of in-
correct circuit output data-bits. In the maximizing
case, the number of correct output data-bits of the
evolved circuit is used as the fitness score. In this
work, we use the minimizing case as stated in Equa-
tion 2, where z is the number of inactive nodes in the
solution circuits.
SL f itness =
(
b when b > 0
b − z otherwise
(2)
This method continues to evolve designs till the num-
ber of generations is exhausted, even if a functionally
correct circuit is found while trying to minimize z. We
minimize the circuit size by minimizing the number
of active gates. However, running the SL configured
CGP method to evolve the best-fit design mandates
millions of generations, especially for realizing non-
linear functions under investigation. Besides, the SL
method adopts a similar hamming distance rule across
all bits, leading to smaller refinements along all the
design paths associated with the output bits. The SL
process ceases to drive major topological changes for
most significant bits (MSBs) associated design paths
and thereby lags in evolving best-fit design solutions
in consolidation with all the output bits of the investi-
gated non-linear functions. BwF attempts to improve
the selection among the available solutions by con-
sidering the weighted fitness across the output bits of
Improving Digital Circuit Synthesis of Complex Functions using Binary Weighted Fitness and Variable Mutation Rate in Cartesian Genetic
Programming
115
5bit x
2
0
0.5
10
20
30
40
259.2
259.4
259.6
259.8
260
0.1
0.2
0.3
0
0.5
0
0.5
0
0.5
0
0.5
5bit x
3
0.5
4000
6000
8000
10000
10000
0.92
0.94
0.96
0.98
0.5 0.5 0.5 0.5
min_Absolute_error
Mean_Absolute_error
max_Absolute_error
Error_Probability
Standard_deviation
Mean_Relative_error
Median_Absolute_error
Mode_Absolute_error
5bit x
4
0.5
100000
150000
200000
250000
300000
500000
600000
700000
800000
0.92
0.94
0.96
0.98
0.5 0.5 0.5 0.5
SL
BwF
Fitness
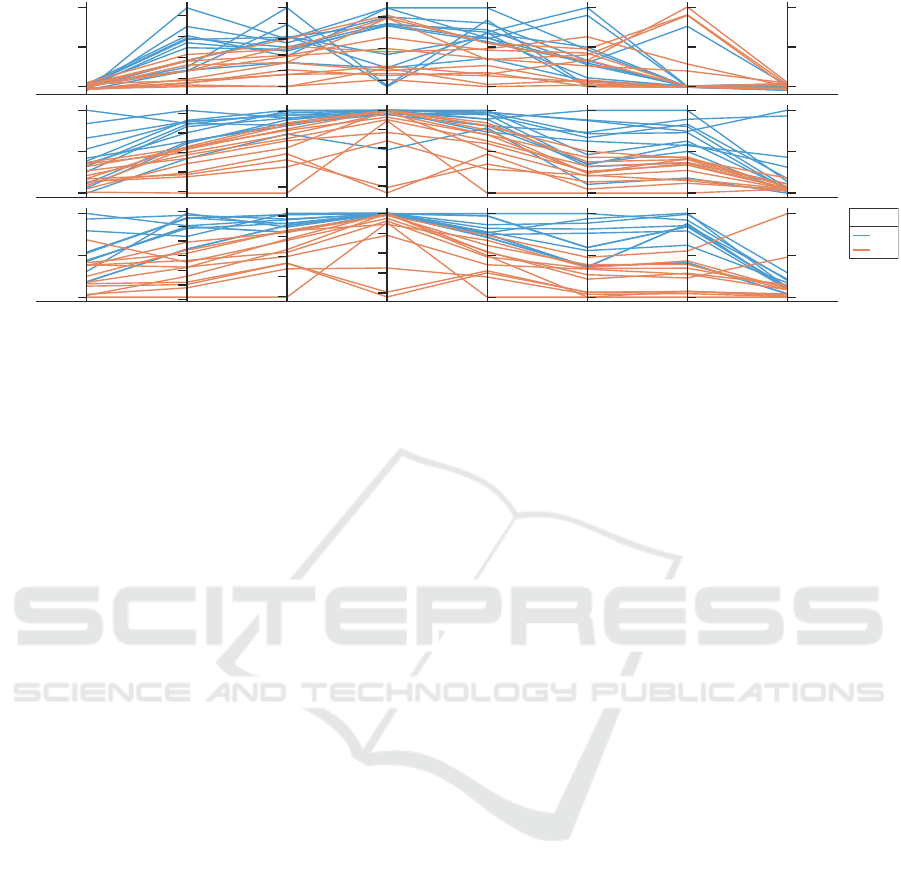
Figure 2: Error metrics comparisons for BwF versus SL methods, when employed with all possible CGP configurations, for
generating 5-bit power functions : x
2
, x
3
, x
4
.
the design evolved instead of considering hamming
distance across all the established output bits. The
BwF fitness function is stated in Equations 3-4. The
binary-weighted sum (BWS) is a weighted score, giv-
ing positional weightage to error in individual output
bits derived from the evolved circuit design (C(O
i
))
when compared with the expected (E(O
i
) functional
output, where i
th
output bit is scaled by the error con-
tributed. BWS is used over all input combinations to
calculate the BwF of a solution. We also include the
term z to minimize the circuit size post a functionally
correct circuit is evolved.
BW S =
n
o
−1
∑
i=0
2
i
× δ
i
(3)
where δ
i
=
(
1 i f O
Exp
(i) 6= O
Cir
(i)
0 i f O
Exp
(i) = O
Cir
(i)
BwF f itness =
(
BW S when BW S > 0
BW S − z otherwise
(4)
5 EXPERIMENTAL RESULTS
In the initial generations, BwF is expected to aid
in selecting the best functionally equivalent topol-
ogy among the solutions, as discussed in section 4.1.
Based on the evaluated fitness score, BwF allows se-
lecting topologies with the least deviation in the out-
put function from the expected function, which oth-
erwise was not possible in the SL method due to its
equal weightage rule associated with the output bits.
The evolution process is slowed with reduced muta-
tions in the later generations, only modifying small
sub-parts of the circuits. Towards the final gener-
ations, BwF continues to evolve the designs at the
gate-level. The BwF adopted CGP along with eVar
mutation rate is observed to not only obtain circuits
with the least deviation from the expected non-linear
function but also to evolve the circuit with fewer gen-
erations, as discussed in the following sections. The
impact of BwF and eVar adoption in CGP is presented
by synthesizing circuits of power functions and acti-
vation functions, which are hard to synthesize other-
wise. Each configuration discussed in section 3 is run
20 times with the same generations limit for different
configurations being compared. For example, 5bit x
3
has 12 configurations of mutation scheme and evolu-
tionary strategy. Both BwF and SL with these 12 con-
figurations are run 20 independent times in an attempt
to obtain the average behaviour of circuits evolved
with the specific configuration. The results discussed
in the following sections are only an illustrative sub-
set of all the experiments, the full comprehensive set
of results is made available in (Prashanth, 2022).
5.1 Error Analysis
Eight different error metrics, including Mean Abso-
lute Error (MAE), Error Probability (EP), Standard
deviation (STD), Mean relative error (MRE), Me-
dian of absolute error (MeAE), Mode of absolute er-
ror (MoAE), Maximum absolute error (Max-AE), and
Minimum absolute error (Min-AE) were investigated
for eVar, and BwF modified CGP and traditional CGP
configurations for the power and activation functions.
ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications
116
0
0.05
0.1
0.15
Function : x
2
2bit
0
1
2
3bit
0
5
10
4bit
0
20
40
60
5bit
0
2
4
6
Function : x
3
0
100
200
500
1000
1500
0
5000
10000
(10,point)
(10,probabilisticOnlyActive)
(10,probabilistic)
(10,single)
(28,point)
(28,probabilisticOnlyActive)
(28,probabilistic)
(28,single)
(55,point)
(55,probabilisticOnlyActive)
(55,probabilistic)
(55,single)
0
10
20
30
Function : x
4
(10,point)
(10,probabilisticOnlyActive)
(10,probabilistic)
(10,single)
(28,point)
(28,probabilisticOnlyActive)
(28,probabilistic)
(28,single)
(55,point)
(55,probabilisticOnlyActive)
(55,probabilistic)
(55,single)
0
500
1000
1500
(10,point)
(10,probabilisticOnlyActive)
(10,probabilistic)
(10,single)
(28,point)
(28,probabilisticOnlyActive)
(28,probabilistic)
(28,single)
(55,point)
(55,probabilisticOnlyActive)
(55,probabilistic)
(55,single)
0
1
2
10
4
(10,point)
(10,probabilisticOnlyActive)
(10,probabilistic)
(10,single)
(28,point)
(28,probabilisticOnlyActive)
(28,probabilistic)
(28,single)
(55,point)
(55,probabilisticOnlyActive)
(55,probabilistic)
(55,single)
0
2
4
10
5
SL
BwF
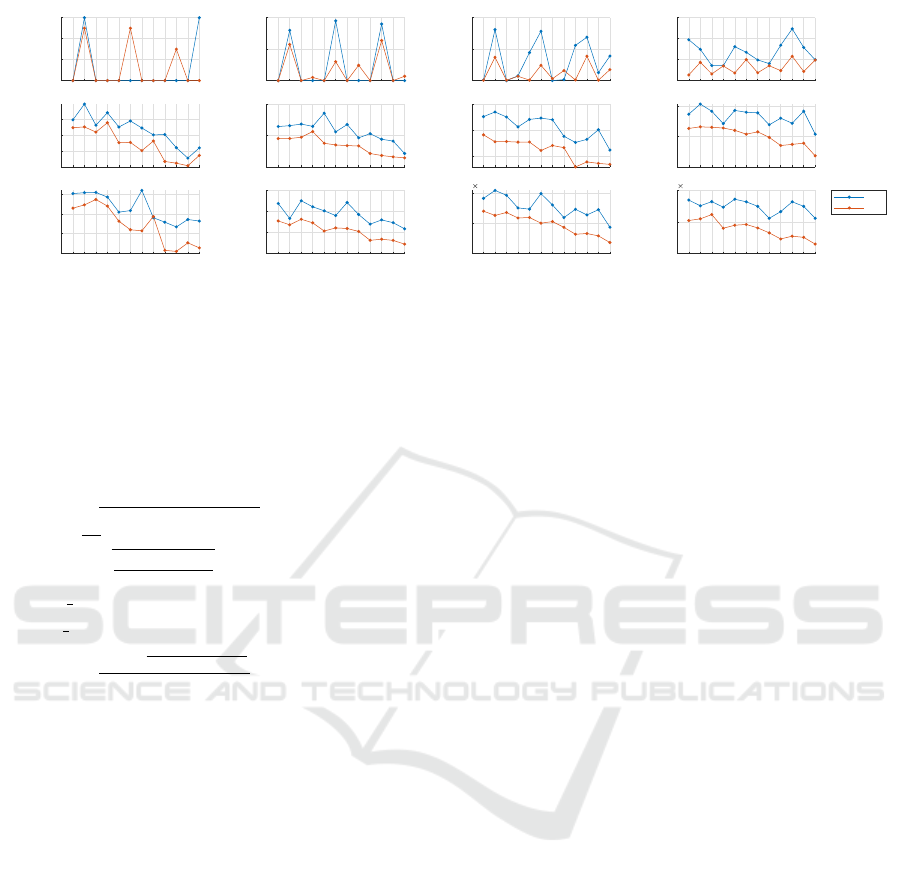
Figure 3: Comparison of CGP configurations w.r.t Mean Absolute Error (in y-axis). Configurations are pairs of evolution-
ary strategy(10 → (1+10), 28 → (2+8), 55 → (5+5) ) and mutation scheme. BwF performs better than SL for all CGP
configurations.
The error metrics are defined in the Equations 5.
EC =
∑
∀x in R
(O
Exp
(x) 6= O
Cir
(x))
MAE =
∑
∀x in R
|O
Exp
(x)−O
Cir
(x)|
2
N
EP =
EC
2
N
ST D =
q
(AE(x)−MAE)
2
2
N
Max AE = max(| O
Exp
(x) − O
Cir
(x) |) ∀x in R
Min AE = min(| O
Exp
(x) − O
Cir
(x) |) ∀x in R
MRE =
∑
∀x in R
|O
Exp
(x)−O
Cir
(x)|
max(1,O
Exp
)
2
N
(5)
The 5-bit data-format for power-two (x
2
), power-three
(x
3
), and power-four (x
4
) functions are shown in Fig-
ure 2 with the proposed eVar and BwF modified CGP.
All three mutation schemes - (1+10), (2+8), and (5+5)
with four different evolutionary strategies - Proba-
bilistic, Probabilistic Only Active, Point and Single
were configured independently to evolve the power
function for 5-bits. Each colored line connecting dif-
ferent error metrics represents the average error met-
rics of 20 runs for a given configuration among the
12 investigated. The SL driven CGP method, which
employs a constant mutation rate, and equal-weighted
fitness showcased higher error metrics for different
evolved circuits when compared to most of the cir-
cuits generated by the proposed eVar and BwF modi-
fied CGP method. The reduced error metrics confirm
that the eVar and BwF configured CGP approach de-
rives fitter circuits than SL based CGP approach.
5.2 CGP Configuration Analysis
Figure 3 shows the comparison between BwF and
SL generated circuits for all the configurations. The
(5+5) evolutionary strategy consistently performs bet-
ter than the (1+10) and (2+8) strategies. The (2+8)
strategy is also found to perform better than (1+10)
strategy. This result hints that creating fewer child
solutions per parent in every generation is preferred.
Fewer children per parent imply a higher number of
circuit topologies are being carried forward to further
generations. The mutation scheme has a large im-
pact on the generated circuits MAE when using SL
fitness function. Furthermore, there is no clear corre-
lation between the mutation type and MAE over the
functions (x
2
, x
3
, x
4
) and bit width. BwF as fitness
function is found to minimise the variation in MAE
with mutation type selected. Single and Point muta-
tion types perform better than Probabilistic and Prob-
abilistic Only Active when BwF is used. BwF across
12 mutation scheme emerges with a clear accuracy
advantage ranging from 5% to 50% of less MAE for
x
3
, and x
4
power functions when compared with SL
method. The same is not established for x
2
power
function, which are smaller designs. Hence BwF is
preferred to realise functions with higher bit-width
and complexity.
6 APPLICATION : ACTIVATION
FUNCTIONS
Activation functions are chosen to showcase the abil-
ity to evolve complex non-linear circuits using the
proposed modifications to CGP. Digital circuits are
usually clocked-sequential designs, requiring Flip-
Flops to maintain intermediate results. Activation
functions are difficult functions to realize in hard-
ware, and tedious design effort is needed to approx-
Improving Digital Circuit Synthesis of Complex Functions using Binary Weighted Fitness and Variable Mutation Rate in Cartesian Genetic
Programming
117
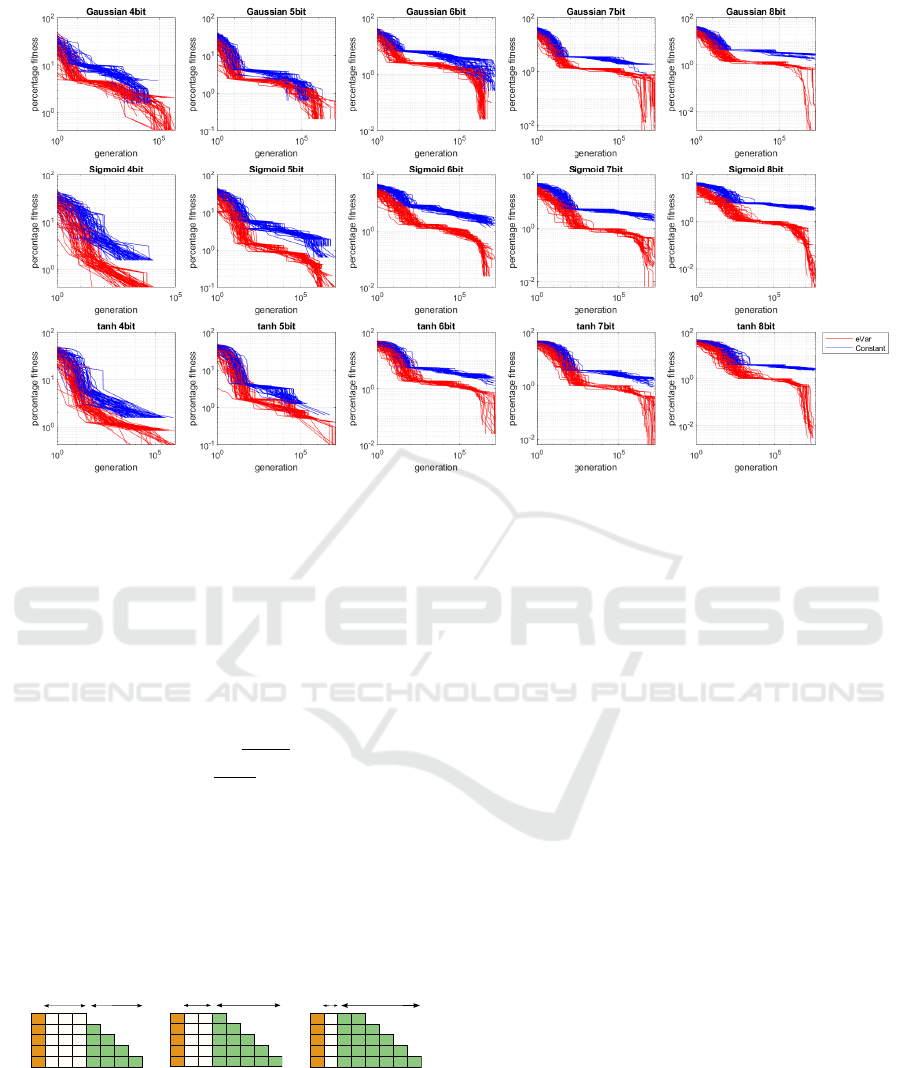
Figure 4: Comparison of convergence to full-fitness of constant mutation rate and exponentially varying mutation rate. Most
eVar-BwF runs converge to functionally-perfect solutions within the generation plotted, while SL-constant mutation rate runs
require more generations.
imate them to sequential designs. Our CGP evolved
circuits are purely combinatorial circuits, which en-
able a large span of hardware-resource (silicon space,
power) to speed of execution trade-off during the syn-
thesis stage of a typical VLSI physical implementa-
tion flow.
Sigmoid(x) =
1
(1+e
−x
)
tanh(x) =
e
x
−e
−x
e
x
+e
−x
Gaussian(x) = e
−x
2
(6)
Sigmoid, Gaussian and Hyperbolic-tangent are de-
scribed in Equation 6. Fixed-point representation of
the data is used to represent the input and outputs of
the activation function. Round-to-floor quantization
scheme is used to obtain the fixed-point representa-
tion of the continuous activation functions. Figure 5
S
Integer
4bit
5bit
6bit
7bit
8bit
fractional
(a)
S
Integer
4bit
5bit
6bit
7bit
8bit
fractional
(b)
S
Integer
4bit
5bit
6bit
7bit
8bit
fractional
(c)
Figure 5: Input data format for (a) Sigmoid, (b) Hyperbolic
tangent, and (c) Gaussian activation functions.
shows the input fixed-point data format used. The out-
put data format for Sigmoid, Hyperbolic-Tangent, and
Gaussian activation function was configured similar
to the input data format of Gaussian function since it
offers adequate integer bits to represent the full range
of output values between -1 to 1. Typical evolutionary
strategy of (1+4) along with Point mutation scheme
was adopted for this analysis.
6.1 Fitness Convergence
Figure 4 is the plot of percentage-of-fitness versus
generations in logarithm scale for Gaussian, Sigmoid,
and hyperbolic-tangent functions of 4-bit to 8-bit
data-formats, when configured with (blue runs) con-
stant mutation rate with SL, and (red runs) eVar mu-
tation rate with BwF. We report the percentage of fit-
ness since the order of magnitude of SL and BwF val-
ues are different. The graph also allows to recognize
potential termination when a functionally perfect so-
lution is found. The eVar mutation rate evolves to
a similar percentage of fitness attained by constant
mutation rate by at least a decade generation less for
lower order bit-widths, and at least 10
5
generations
less for 7, and 8-bit activation functions. Additionally,
the best evolved design for eVar based CGP consis-
tently achieved maximum fitness for a similar number
of generations throughout the three activation func-
tions investigated. Considering the evolved design at
the last generation, the percentage of fitness achieved
by the eVar applied CGP is better by at least a decade
for lower order bit-width functions and at least 100
ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications
118
times better for the 7 and 8-bit activation functions.
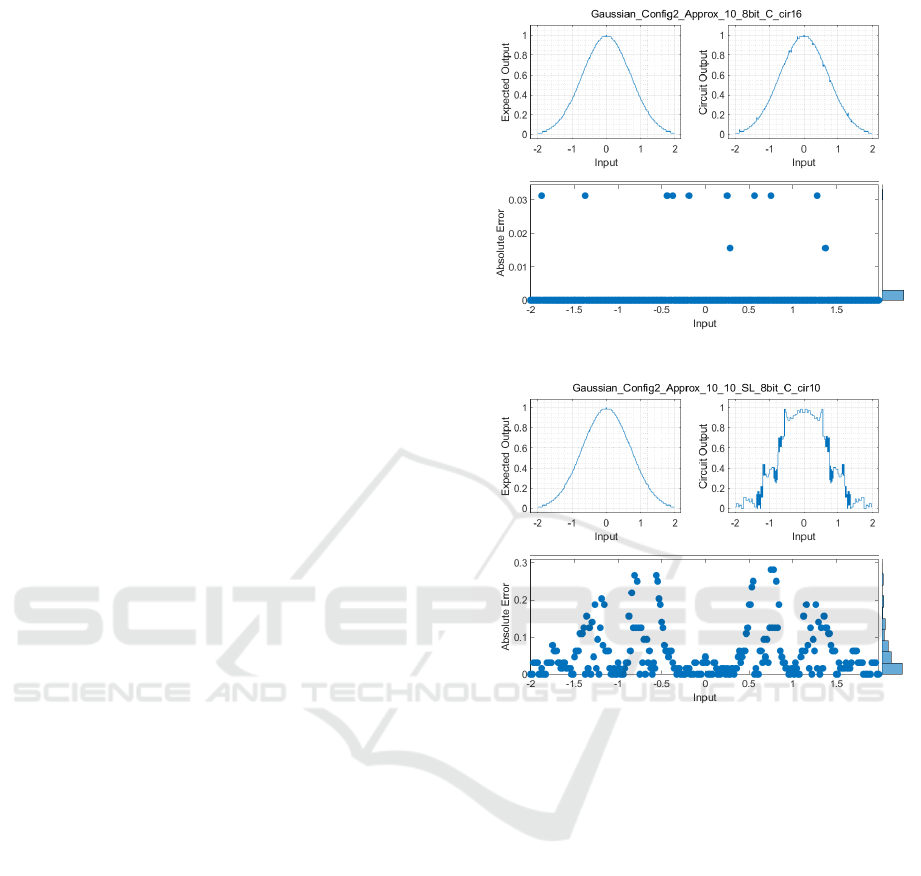
6.2 Correlation of Circuit Output
Figure 6 (a) shows the output profile of the circuit
generated from the proposed scheme, which closely
resembles the expected output non-linear profile. The
absolute error remains zero for most of the input data,
with dominant error values close to 0. Figure 6 (b)
depicts the output profile of the circuit generated from
the traditional SL method. It demonstrates erroneous
output for different input data. The absolute error is
not only spread across the input data range but also
higher in magnitude. The error rate is also higher
compared to the proposed BwF-and-eVar modified
CGP approach. The error rate for both methods are
indicated next to the absolute error graphs.
7 CONCLUSIONS
The circuits evolved from the proposed BwF and eVar
method were synthesised faster and provided gate-
level designs that furnished close to the exact out-
put. The eVar mutation rate explores the design space
much faster to evolve to a functionally correct solu-
tion. The BwF feature supports selecting and driv-
ing the evolutionary designs toward weighted fitness
along the output bits, leading to reduced error met-
rics when compared with SL technique. Among the
evolutionary strategies (5+5) is preferred, consider-
ing the lowest gate count and securing the best fit-
ness among the three strategies configured for realis-
ing power functions. BwF achieves fitness improve-
ment in terms of lower MAE ranging from 5% to 50%
for x
3
andx
4
functions when compared with the SL
method. The proposed eVar and BwF modified CGP
was applied on activation functions such as Gaussian,
Sigmoid, and hyperbolic-tangent to validate the effec-
tiveness of the modifications. For 7-bit and 8-bit acti-
vation functions, eVar aids in evolving the circuit de-
sign faster by atleast 10
5
times lesser generations, and
BwF generates output profile close to required profile
when compared to SL. BwF and eVar enabled CGP
evolved circuits adhere closely to the non-linear pro-
file of the activation functions studied in this work.
Overall, BwF and eVar are two major tools in setting
up CGP to evolve complex non-linear functions with
significantly less computation effort. All the designs
are made freely available in (Prashanth, 2022) for fur-
ther usage by the research and designers community.
(a)
(b)
Figure 6: Circuit and expected output 8bit Gaussian CGP
run example. (a) BwF helps to obtain circuits which closely
resemble non-linear functions. (b) SL only considers ham-
ming distance without assigning weightage to large errors.
REFERENCES
Berndt, A., Campos, I. S., Lima, B., Grellert, M., Carvalho,
J. T., Meinhardt, C., and De Abreu, B. A. (2021). Ac-
curacy and size trade-off of a cartesian genetic pro-
gramming flow for logic optimization. In 2021 34th
SBC/SBMicro/IEEE/ACM Symposium on Integrated
Circuits and Systems Design (SBCCI), pages 1–6.
Brayton, R. and Mishchenko, A. (2010). Abc: An aca-
demic industrial-strength verification tool. In Touili,
T., Cook, B., and Jackson, P., editors, Computer
Aided Verification, pages 24–40, Berlin, Heidelberg.
Springer Berlin Heidelberg.
Fi
ˇ
ser, P., Schmidt, J., Va
ˇ
s
´
ı
ˇ
cek, Z., and Sekanina, L. (2010).
On logic synthesis of conventionally hard to synthe-
size circuits using genetic programming. In 13th IEEE
Symposium on Design and Diagnostics of Electronic
Improving Digital Circuit Synthesis of Complex Functions using Binary Weighted Fitness and Variable Mutation Rate in Cartesian Genetic
Programming
119

Circuits and Systems, pages 346–351.
Hodan, D., Mrazek, V., and Vasicek, Z. (2020).
Semantically-oriented mutation operator in cartesian
genetic programming for evolutionary circuit design.
In Proceedings of the 2020 Genetic and Evolution-
ary Computation Conference, GECCO ’20, page
940–948, New York, NY, USA. Association for Com-
puting Machinery.
Hrb
´
a
ˇ
cek, R. and Drahosova, M. (2013). Coevolutionary
cartesian genetic programming in fpga.
Kocnova, J. and Vasicek, Z. (2020). Ea-based resynthe-
sis: An efficient tool for optimization of digital cir-
cuits. Genetic Programming and Evolvable Machines,
21(3):287–319.
Manazir, A. and Raza, K. (2019). Recent developments in
cartesian genetic programming and its variants. ACM
Comput. Surv., 51(6).
Miller, J. (2020). Cartesian genetic programming: its sta-
tus and future. Genetic Programming and Evolvable
Machines, 21.
Miller, J. F. and Harding, S. L. (2008). Cartesian ge-
netic programming. In Proceedings of the 10th An-
nual Conference Companion on Genetic and Evolu-
tionary Computation, GECCO ’08, page 2701–2726,
New York, NY, USA. Association for Computing Ma-
chinery.
Mishchenko, A., Chatterjee, S., and Brayton, R. (2006).
Dag-aware aig rewriting a fresh look at combina-
tional logic synthesis. In Proceedings of the 43rd An-
nual Design Automation Conference, DAC ’06, page
532–535, New York, NY, USA. Association for Com-
puting Machinery.
Miyasaka, Y., Zhang, X., Yu, M., Yi, Q., and Fujita, M.
(2021). Logic synthesis for generalization and learn-
ing addition. In 2021 Design, Automation & Test
in Europe Conference & Exhibition (DATE), pages
1032–1037.
Prashanth, H. C. (2022). Results website. https://sites.
google.com/view/bwf-evar/home.
Prashanth, H. C. and Rao, M. (2022). Evolutionary stan-
dard cell synthesis of unconventional designs. In Pro-
ceedings of the Great Lakes Symposium on VLSI 2022,
GLSVLSI ’22, page 189–192, New York, NY, USA.
Association for Computing Machinery.
Sekanina, L., Ptak, O., and Vasicek, Z. (2014). Cartesian
genetic programming as local optimizer of logic net-
works. In 2014 IEEE Congress on Evolutionary Com-
putation (CEC), pages 2901–2908.
Thierens, D. (2002). Adaptive mutation rate control
schemes in genetic algorithms. In Proceedings of
the 2002 Congress on Evolutionary Computation.
CEC’02 (Cat. No.02TH8600), volume 1, pages 980–
985 vol.1.
Va
ˇ
s
´
ı
ˇ
cek, Z. and Sekanina, L. (2012). Hardware acceler-
ator of cartesian genetic programming with multiple
fitness units. COMPUTING AND INFORMATICS,
29(6+):1359–1371.
Vasicek, Z. (2015). Cartesian gp in optimization of com-
binational circuits with hundreds of inputs and thou-
sands of gates. In Machado, P., Heywood, M. I., Mc-
Dermott, J., Castelli, M., Garc
´
ıa-S
´
anchez, P., Burelli,
P., Risi, S., and Sim, K., editors, Genetic Program-
ming, pages 139–150, Cham. Springer International
Publishing.
Vasicek, Z. and Sekanina, L. (2016). Search-based syn-
thesis of approximate circuits implemented into fpgas.
In 2016 26th International Conference on Field Pro-
grammable Logic and Applications (FPL), pages 1–4.
ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications
120
