Approaches for Rule Discovery in a Learning Classiﬁer System

Michael Heider

, Helena Stegherr

, David P

atzel

, Roman Sraj, Jonathan Wurth

Benedikt Volger and J

org H

ahner

Universit

at Augsburg, Am Technologiezentrum 8, Augsburg, Germany

ﬁ

Keywords:

Rule Set Learning, Rule-based Learning, Learning Classiﬁer Systems, Evolutionary Machine Learning,

Interpretable Models, Explainable AI.

Abstract:

To ﬁll the increasing demand for explanations of decisions made by automated prediction systems, machine

learning (ML) techniques that produce inherently transparent models are directly suited. Learning Classiﬁer

Systems (LCSs), a family of rule-based learners, produce transparent models by design. However, the use-

fulness of such models, both for predictions and analyses, heavily depends on the placement and selection

of rules (combined constituting the ML task of model selection). In this paper, we investigate a variety of

techniques to efﬁciently place good rules within the search space based on their local prediction errors as well

as their generality. This investigation is done within a speciﬁc LCS, named SupRB, where the placement of

rules and the selection of good subsets of rules are strictly separated in contrast to other LCSs where these

tasks sometimes blend. We compare a Random Search, (1, λ)-ES and three Novelty Search variants. We ﬁnd

that there is a deﬁnitive need to guide the search based on some sensible criteria, i.e. error and generality,

rather than just placing rules randomly and selecting better performing ones but also ﬁnd that Novelty Search

variants do not beat the easier to understand (1,λ)-ES.

1 INTRODUCTION

With the ever increasing automation in many

socio-technical settings, such as manufacturing, au-

tonomous decisions of agents are more common than

ever. This advent of more independent and intelli-

gent technical systems holds great potentials in in-

creasing safety and comfort of workers as well as gen-

eral productivity. However, the roll-out of such sys-

tems can be held back when stakeholders, from op-

erator to management level, do not trust that the sys-

tems perform on-par or even better than their human

counterparts. Therefore, agents are required to give

those stakeholders sensible explanations and insights

into their decision making processes. (Heider et al.,

2022a)

For the machine learning components of such

agents, this means that they should offer strong inter-

pretability, self-explaining or transparency-by-design

capabilities. Recently, the use of Learning Classi-

https://orcid.org/0000-0003-3140-1993

https://orcid.org/0000-0001-7871-7309

https://orcid.org/0000-0002-8238-8461

https://orcid.org/0000-0002-5799-024X

https://orcid.org/0000-0003-0107-264X

ﬁer Systems (LCSs) (Urbanowicz and Moore, 2009)

in such scenarios was proposed by (Heider et al.,

2021). They argue that LCSs are uniquely suited

as this family of rule-based learning algorithms fea-

tures both powerful machine learning capabilities in

all commonly encountered settings as well as inher-

ently transparent models that follow human thought

processes due to their rule-like structure. Rules in an

LCS are of an if-then form, where the if (or condi-

tion) constricts the section of the feature space this

rule applies to (matches) and the then contains a sim-

pler, therefore more comprehensible, local model able

to predict data points from that feature space partition.

Conditions are usually optimized using a stochastic

search heuristic, such as evolutionary algorithms. The

model’s practical transparency (or explainability in a

broader context) is primarily inﬂuenced by the num-

ber of rules present and their placement within the

feature space (the two tasks that constitute model

selection in rule-based machine learning). There-

fore, the—as optimal as possible—placement of rules

should be a primary concern when designing an LCS

algorithm with explainability requirements.

In this work, we expand the Supervised Rule-

based learning system (SupRB) (Heider et al., 2022b),

Heider, M., Stegherr, H., Pätzel, D., Sraj, R., Wurth, J., Volger, B. and Hähner, J.

Approaches for Rule Discovery in a Learning Classiﬁer System.

DOI: 10.5220/0011542000003332

In Proceedings of the 14th International Joint Conference on Computational Intelligence (IJCCI 2022), pages 39-49

ISBN: 978-989-758-611-8; ISSN: 2184-3236

a recently proposed LCS for regression tasks, with

different methods to discover new rules that ﬁt the

data well and benchmark them against each other on

a variety of real world datasets.

2 LEARNING CLASSIFIER

SYSTEMS AND RULE

DISCOVERY

As previously introduced, LCSs are a family of—

typically evolutionary—rule-based learning systems

with a long research history (Urbanowicz and Moore,

2009; Urbanowicz and Browne, 2017). Traditionally,

they are categorized into two approaches:

• Michigan-style systems which feature strong on-

line learning capabilities and have evolved from

reinforcement learning (RL) to all major learning

schemes. They consist of a single population of

rules on which the optimizer operates directly.

• Pittsburgh-style systems that typically perform of-

ﬂine batch learning and primarily focus on super-

vised learning and feature a population of sets of

rules, where the optimizer operates on those sets

rather than the rules individually.

Due to those very different outsets, their approach

to rule discovery and improvement differs substan-

tially. For example, the most widespread Michigan-

style system, the XCS classiﬁer system (Wilson,

1995), does feature two mechanisms to determine a

new rule. The ﬁrst is the covering mechanism. When

the number of rules that match a new data point falls

below a predetermined threshold, new rules are gen-

erated that match this data point. These rules are often

randomly made more general than to just match this

point speciﬁcally and therefore slightly differ when

inserted into the population of rules. The second is

the evolutionary algorithm. It is invoked on match-

ing rules that also propose the chosen action (e.g. fol-

lowing an epsilon-greedy policy in RL). It utilizes

crossover and mutation mechanisms appropriate for

the types of input data and evolves the population in a

steady-state manner.

For Pittsburgh-style systems, new rules can be di-

rectly added to an individual of the population (a set

of rules), shared between individuals or be the product

of a mutation (and more rarely rule-level crossover)

operator. As the evolutionary algorithm of these sys-

tems operates on rule sets rather than rules directly,

the ﬁtness signal that guides evolution is not based

on individual rule performance but rather the perfor-

mance of a given set of rules, which can complicate

rule discovery due to the added indirection.

3 THE SUPERVISED

RULE-BASED LEARNING

SYSTEM

The Supervised Rule-based learning system (SupRB)

(Heider et al., 2022b) is an LCS with alternating

phases of rule discovery and solution composition

(additional details in (Heider et al., 2022c)). The two

phases combined solve the standard machine learning

task of model selection for an LCS. Splitting these

phases allows a more direct control of the optimiza-

tion process as objectives are more directly related

to overall behaviour. In contrast, in Pittsburgh-style

systems a model’s ﬁtness that also controls changes

made to its rules follows the interaction of its rules

rather than their individual suitability, whereas, in

Michigan-style systems, rule ﬁtness often depends on

their neighbouring rules (niching) and, due to their

online learning nature, does not necessarily relate to

the full dataset. In the rule discovery (RD) phase of

SupRB, new rules are generated and locally optimized

to produce a diverse pool of general rules that exhibit

low errors. Subsequently, in the solution composition

(SC) phase, an optimizer attempts to select a well per-

forming subset of the discovered rules. This subset

should be small (exhibiting low complexity) but also

produce a model (by mixing rules in areas of over-

lap) with a low prediction error. There is an obvi-

ous tradeoff between those two objectives (as was be-

tween general and accurate rules during RD). Thus,

balancing these objectives highly depends on the use

case at hand and the inherent requirements into expla-

nations and model readability. In some cases, larger

models might be acceptable, whereas, in others, e.g.

when decisions need to be made fast, smaller models

with less overlap are preferred.

The alternation between phases (rather than hav-

ing a very long RD phase followed by an SC phase)

allows to use additional information and guide the op-

timizers better. When discovering new rules, the RD

mechanism places new rules more likely where the

last elitist from the SC process showed high predic-

tion errors. This can allow to ﬁll unmatched areas (or

areas of ill-ﬁt local models) in the overall model that

might otherwise go unnoticed. Blindly ﬁtting a mul-

titude of rules would become quite expensive as the

whole dataset needs to be matched and then batch-

learned multiple times. Additionally, it is hard to de-

termine beforehand how many rules would be needed

in the pool to ﬁnd a satisfactory subset that solves the

learning task.

SupRB’s model is kept as simple and interpretable

as possible as its transparency is a central aspect (Hei-

der et al., 2022b):

ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications

1. Rules’ conditions use an interval based matching:

A rule k applies for example x iff x

∈ [l

k,i

]∀i

with l being the lower and u the upper bounds.

2. Rules’ local models f

(x) are linear. They are

ﬁt using linear least squares with a l2-norm reg-

ularization (Ridge Regression) on the subsample

matched by the respective rule.

3. When mixing multiple rules to make a predic-

tion, a rule’s experience (the number of examples

matched during training and therefore included in

ﬁtting the submodel) and in-sample error are used

in a weighted sum.

For the SC phase optimizer, we use a genetic al-

gorithm (GA) for all experiments in this paper. It op-

erates directly on a bitmap corresponding to whether

a rule from the pool is part of this solution to the

learning task at hand or whether it is not. In previ-

ous work by (Wurth et al., 2022) other metaheuristic

optimizers were tested to compose solutions. They

found that the choice of metaheuristic is—given suf-

ﬁcient computational budget—largely dependent on

the learning task, although even there, differences

were small, which makes the GA a ﬁtting choice.

This is also the more traditional option as LCSs typi-

cally feature evolutionary computation methods. Par-

ent (groups of two) selection is done using tourna-

ment selection. Those parents are recombined with

an n-point crossover under a 90% probability. The

children are then mutated using a probabilistic bit-ﬂip

mutation. These children form the new population

together with the ﬁttest parents (elitism). In our ex-

periments we used a population size of 32 children

and 5 to 6 elitists. An individual’s (solution to the

learning task) ﬁtness is determined based on its in-

sample prediction error and its complexity (number of

rules present) following (Heider et al., 2022b). Criti-

cally, this phase does not affect the position of rules’

bounds. Individuals can only be composed of rules

in the pool and those rules remain unchanged by the

GA’s operators.

The main subject of this paper is the RD phase’s

optimizer. In contrast to many typical optimization

problems we do not want to ﬁnd the singular glob-

ally optimal rule but rather a set of localized rules that

perform well in this particular feature space partition,

thus, we are attempting to ﬁnd an unknown number of

local optima without mapping the entire ﬁtness land-

scape. The rules discovered should be a diverse set

and we can allow overlapping rules as SC will se-

lect the subset of discovered rules most appropriate

to solve the learning task. As for the SC, a variety of

different optimizers can achieve this. In the follow-

ing, the ﬁve different optimization approaches for RD

that will be compared in the remainder of this paper

are presented. For all heuristics we utilize the same

approach for calculating rule ﬁtness by combination

of two objectives, utilizing the in-sample error and

the matched feature space volume, respectively—cf.

(Heider et al., 2022b).

3.1 Evolution Strategy

As discussed before, LCSs traditionally apply some

evolutionary algorithm for their optimization pro-

cesses. Therefore, the ﬁrst strategy employed for RD

in SupRB, which was also used for the experiments

in (Wurth et al., 2022), is an Evolution Strategy (ES)

(Heider et al., 2022b), speciﬁcally, a simpliﬁed (1,λ)-

ES. The initial individual for the ES is generated by

placing a rule at a randomly selected training exam-

ple, preferring those examples where the in-sample

error is high in the intermediate global solution. This

individual serves as the initial candidate for addition

to the pool and the parent. From the parent, λ children

are generated, each mutated by a non-adaptive oper-

ator which moves the upper and lower bounds fur-

ther outwards by adding values sampled from a half-

normal distribution. The parent for the next gener-

ation is the child individual with the highest ﬁtness.

If this individual showed a better ﬁtness than the cur-

rent candidate it also becomes the new candidate. The

evolutionary search terminates when for a ﬁxed num-

ber of generations no new candidate has been found.

This ES produces one rule at a time but can easily

be parallelized. One merit of this approach is in the

explainability of both the search procedure and the re-

sulting pool. In general, rules that have ﬁtnesses inde-

pendent from other rules are easier to understand for

most non-experts. Whereas, in most current LCSs,

the ﬁtness assigned to a rule is highly dependent on

what other rules it is surrounded by. Beyond ﬁtness-

based considerations on the understandability of our

approach, the ES is also a quite easy to follow search

method: Expand the area (or hypervolume) an indi-

vidual matches, evaluate the new individuals, choose

the best new option and repeat.

3.2 Random Search

As an alternative to the strongly ﬁtness-guided RD

performed by the ES, Random Search (RS) is intro-

duced. RS commonly serves as a baseline for test-

ing the performance of other optimization algorithms.

Furthermore, with the ulterior motive of ﬁnding di-

verse rules to add to the pool, RS provides an inter-

esting approach where the ﬁtness only plays a role in

the selection of the ﬁnal candidate, but not in the gen-

eration of new rules.

Approaches for Rule Discovery in a Learning Classiﬁer System

In SupRB, RS, similarly to ES, randomly selects

a ﬁxed number of data points weighted by their re-

spective in-sample prediction errors in the last solu-

tion candidate (produced by the previous SC phase).

We then place random bounds around those points

based on half-normal distributions (to ensure we al-

ways match the selected point). To balance the com-

putational cost between RD approaches, we produce

substantially more rules initially than we would in an

ES generation. We then greedily select the rule with

the highest ﬁtness to become part of the pool.

3.3 Novelty Search

One of the central issues of RD is that the optimizer

is tasked to ﬁnd multiple rules that partition the fea-

ture space and, in their individual area, predict data

points well, whereas in many typical optimization

problems the optimizer would be expected to ﬁnd a

single global optimum (or at least a point very close to

it). This task the optimizer has to complete can some-

what be viewed as being tasked to map the larger local

optima within the search space. We aim at ﬁnding a

diverse set of good rules, each within their speciﬁc

area.

In this section, we describe an approach based on

Lehman’s Novelty Search (NS) (Lehman, 2012). In

this evolutionary search method the optimizer is not

(or not fully) guided by the typical ﬁtness function

but rather tries to ﬁnd individuals that exhibit new be-

haviour previously unknown within the population.

Mapped to our case, where we want to ﬁnd a rule

that predicts an area of the feature space currently

unmatched or only matched by rules with high er-

rors in this area, behaviour of rules can be equated to

what subsample of the training data they match. For

our adaptation, we base the NS on a (µ , λ)-ES with

elitism and follow the extensive experimental ﬁndings

laid out by (Gomes et al., 2015). In each iteration, we

select a list of λ parents out of the current population.

These parents are paired, undergo a uniform crossover

and a half-normal mutation (cf. Section 3.1). The re-

sulting children are then ﬁtted and the best performing

µ children are selected for the next population. Addi-

tionally, we select a number of high-performing par-

ents equal to the number of rules the NS is expected to

produce within one RD phase as part of the new pop-

ulation (elitism). Performance of an individual can be

based on novelty alone or on a combination of ﬁtness

(as used in the ES; cf. Section 3.1) and novelty, e.g. a

linear combination. For the novelty of a rule, we com-

pare its match set and the match sets of the other rules

in the pool and the current NS population (the other

children for the selection or the parents for elitism,

respectively). The novelty score assigned to a rule is

the average Hamming-distance between its match set

and its k nearest neighbours’ (most similar rules). k is

set to 15; a value typically encountered with other NS

applications in literature—e.g. (Lehman and Stanley,

2010). After a set number of iterations, we add a set

number of rules to the pool and conclude this phase.

Which rules get added can be randomized or based on

the highest novelty(-ﬁtness combination).

In addition to the basic NS, we implemented and

experimented with two variants: Minimal Criteria

Novelty Search (MCNS) (Lehman and Stanley, 2010;

Lehman, 2012) and Novelty Search with Local Com-

petition (NSLC) (Lehman, 2012).

MCNS imposes additional pressure on the search

to explore less vividly and focus more on rules that

at least fulﬁl some minimal requirement. In our ex-

periments, we set the minimal criterion to a minimum

number (tuned between 10 and 20) of examples from

the training data having to be matched by the rule to

become viable. Although, we did also impose that at

most one fourth of the population should be removed

because they missed the minimal criterion to prevent

collapsing gene pools. We also use progressive mini-

mal criteria novelty search (Gomes et al., 2012), itself

based on MCNS, as an option for combining ﬁtness

and novelty as the objective. Here, all individuals that

do exhibit a ﬁtness worse than the median ﬁtness are

removed automatically in each iteration of the search.

This approach is not tied to MCNS and can be used in

all three variants.

NSLC introduces a localised ﬁtness-based pres-

sure on the new generation. The idea is that, within

a neighbourhood (based on their behaviour and not

their position in the search space) of similar rules, the

rules that exhibit high ﬁtnesses should be chosen. A

rule’s novelty score gets increased by a factor of b/κ,

where b is the number of individuals within the neigh-

bourhood speciﬁed by κ that have a worse ﬁtness than

the rule currently evaluated. We chose κ to be equal

to k as this already does specify a neighbourhood of

rules this rule is in competition with.

One disadvantage of NS-like approaches is that

rule selection is no longer solely based on indepen-

dent metrics (ﬁtness) but rather on the independent

ﬁtness and the highly dependent (on other rules) nov-

elty score.

4 EVALUATION

To examine the differences between the rule dis-

covery methods and to ﬁnd the most versatile strategy,

ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications

we evaluated those strategies within SupRB on

several regression datasets.

4.1 Experiment Design

SupRB is implemented

in Python 3.9, adhering to

scikit-learn (Pedregosa et al., 2011) conventions. In-

put features are transformed into the range [−1, 1],

while the target is standardized. Both transforma-

tions are reversible but improve SupRB’s training pro-

cess as they help preventing rules to be placed in re-

gions where no sample could be matched and remove

the need to tune error coefﬁcients in ﬁtness calcula-

tions, respectively. Based on our assumptions about

the number of rules needed, 32 cycles of alternat-

ing rule discovery and solution composition are per-

formed, generating four (or 8 in case of NS vari-

ants) rules in each cycle for a total of 128 (256 for

NS variants) rules. Additionally, the GA is con-

ﬁgured to perform 32 iterations with a population

size of 32. To tune some of the more sensitive pa-

rameters, we performed a hyperparameter search us-

ing a Tree-structured Parzen Estimator in the Optuna

framework (Akiba et al., 2019) that optimizes aver-

age solution ﬁtness on 4-fold cross validation. We

tuned the optimizers on each dataset independently

for a ﬁxed tuning budget of 360 core hours. The ﬁnal

evaluation, for which we report results in Section 4.2,

uses 8-split Monte Carlo cross-validation, each with

25% of samples reserved as a validation set. Each

learning algorithm is evaluated with 8 different ran-

dom seeds for each 8-split cross-validation, resulting

in a total of 64 runs.

Table 1: Overview of the regression datasets the ﬁve rule

discovery approaches for SupRB are compared on.

Name n

dim

sample

Combined Cycle Power Plant 4 9568

Airfoil Self-Noise 5 1503

Concrete Strength 8 1030

Energy Efﬁciency Cooling 8 768

We evaluate on four datasets part of the UCI Ma-

chine Learning Repository (Dua and Graff, 2017).

An overview of sample size and dimensionality is

given in Table 1. The Combined Cycle Power Plant

(CCPP) (Kaya and T

ufekci, 2012; T

ufekci, 2014)

dataset shows an almost linear relation between fea-

tures and targets and can be acceptably accurately

predicted using a single rule. Airfoil Self-Noise

Recent code at: https://github.com/heidmic/suprb. The

speciﬁc version of the code used in this paper can be found

at: https://doi.org/10.5281/zenodo.7059913.

(ASN) (Brooks et al., 1989) and Concrete Strength

(CS) (Yeh, 1998) are both highly non-linear and will

likely need more rules to predict the target sufﬁ-

ciently. The CS dataset has more input features than

ASN but is easier to predict overall. Energy Efﬁ-

ciency Cooling (EEC) (Tsanas and Xifara, 2012) is

another rather linear dataset, but has a much higher

input features to samples ratio compared to CCPP. It

should similarly be possible to model it using only

few rules.

4.2 Results

In the following we abbreviate SupRB using X as RD

method simply by X.

The means and standard deviations of model per-

formances (measured using the—standardized indi-

vidually per dataset—mean squared error on test data

(MSE)) and model complexities (measured by the

number of rules in the ﬁnal elitist) achieved by the

ﬁve RD approaches when evaluated—as described in

the previous section—on the four real-world datasets

are given in Tables 2 and 3. At ﬁrst glance, on all four

datasets, RS shows the worst performance in terms of

mean MSE and, with the exception of CS, the mod-

els it creates also have the highest model complexity.

The other four optimization approaches vary in their

results between datasets.

In order to get a better overview as well as include

distributional information, we create violin plots to

visualize the MSE results (Figure 1). It can be seen

that, on CCPP (top left in Figure 1), the distributions

of MSE values achieved look very similar, with NS

and NSLC maybe having a very slight edge (consider

the y axis scale) which is not visible in the rounded

mean and standard deviations given in Table 2. For

the ASN dataset, the corresponding violin plot (top

right in Figure 1) as well as the values in Table 2

suggest that ES outperforms the other optimizers and

NSLC is slightly better than NS and MCNS. How-

ever, with respect to model complexity (Table 3), we

observe inverse results: NS and MCNS depict a sim-

ilarly low model complexity, while the mean number

of rules in the solutions found by NSLC, ES and RS

is higher by more than ten. When regarding the CS

dataset, Table 2 and Figure 1 (bottom left) hint to-

wards NSLC being the best of the considered meth-

ods with ES, NS and NSLC performing similarly to

each other but slightly worse than NSLC. In terms of

model complexity (Table 3), this is, again, reversed:

ES, NS and MCNS are similar once more and re-

sult in less complex solutions than NSLC. For the

last dataset, EEC, ES is indicated again as the best

performing method (bottom right in Figure 1). The

Approaches for Rule Discovery in a Learning Classiﬁer System

ES RS NS MCNS NSLC

0.06

0.07

0.08

CCPP

ES RS NS MCNS NSLC

0.1

0.2

0.3

ASN

ES RS NS MCNS NSLC

RD method

0.1

0.2

0.3

MSE

ES RS NS MCNS NSLC

0.00

0.05

0.10

EEC

Figure 1: Standardized (per task) mean squared errors (MSEs) achieved by the different RD methods on the different tasks.

Table 2: Mean and standard deviation (over 64 runs, rounded to two decimal places) of MSE achieved by the ﬁve RD

approaches on the four datasets. Best entry in each row (if one exists) marked in bold.

ES RS NS MCNS NSLC

CCPP 0.07 ± 0.00 0.07 ± 0.00 0.07 ± 0.00 0.07 ± 0.00 0.07 ± 0.00

ASN 0.16 ± 0.03 0.23 ± 0.03 0.22 ± 0.02 0.23 ± 0.02 0.20 ± 0.02

CS 0.14 ± 0.04 0.17 ± 0.03 0.13 ± 0.02 0.13 ± 0.02 0.12 ± 0.02

EEC 0.03 ± 0.01 0.06 ± 0.02 0.04 ± 0.01 0.04 ± 0.01 0.04 ± 0.01

model complexity, however, is lower for NSLC and

much lower for NS and MCNS.

Overall, the visual analysis combined with the

rounded statistics of mean and standard deviation

are not capable of providing us with a conclusive

answer regarding which of the RD methods should

be preferred on tasks like the ones considered. We

thus investigate the data gathered more closely using

Bayesian data analysis

We start by applying to our data the model pro-

posed by Calvo et al. (Calvo et al., 2018; Calvo et al.,

2019) which, for each of the RD methods, provides

us with the posterior distribution over the probabil-

ity of that RD method performing best. We apply this

model to both the MSE observations as well as the

model complexity observations and provide box plots

(Figures 2 and 3) which show the most relevant distri-

bution statistics. Both ﬁgures show that the distribu-

tions over the probabilities of performing the best are

rather tight. However, the ﬁgures also show that there

We deliberately do not use null hypothesis signiﬁ-

cance tests due to their many ﬂaws and possible pitfalls—cf.

e.g. (Benavoli et al., 2017).

cannot be made a very conﬁdent conclusive statement

for a single RD method given the data available: For

both metrics, the highest expected value for the proba-

bility of being the best assigned by the model to a sin-

gle RD method is only around 40 % (to illustrate: this

means that the probability of that candidate not being

the best is around 60 %). Due to this, we also consid-

ered the probability distribution over the probability

of either ES or NSLC performing the best MSE-wise

since those were the highest probability candidates

with respect to that metric. As can be seen, for MSE,

the probability of either of the two being ranked the

best is still merely around 60 % which still does not

amount to much evidence. Only if we include the top

three options (ES, NSLC and NS), are we entering the

region of over 80 % where we could say with some

slight conﬁdence that the best-performing is among

those three.

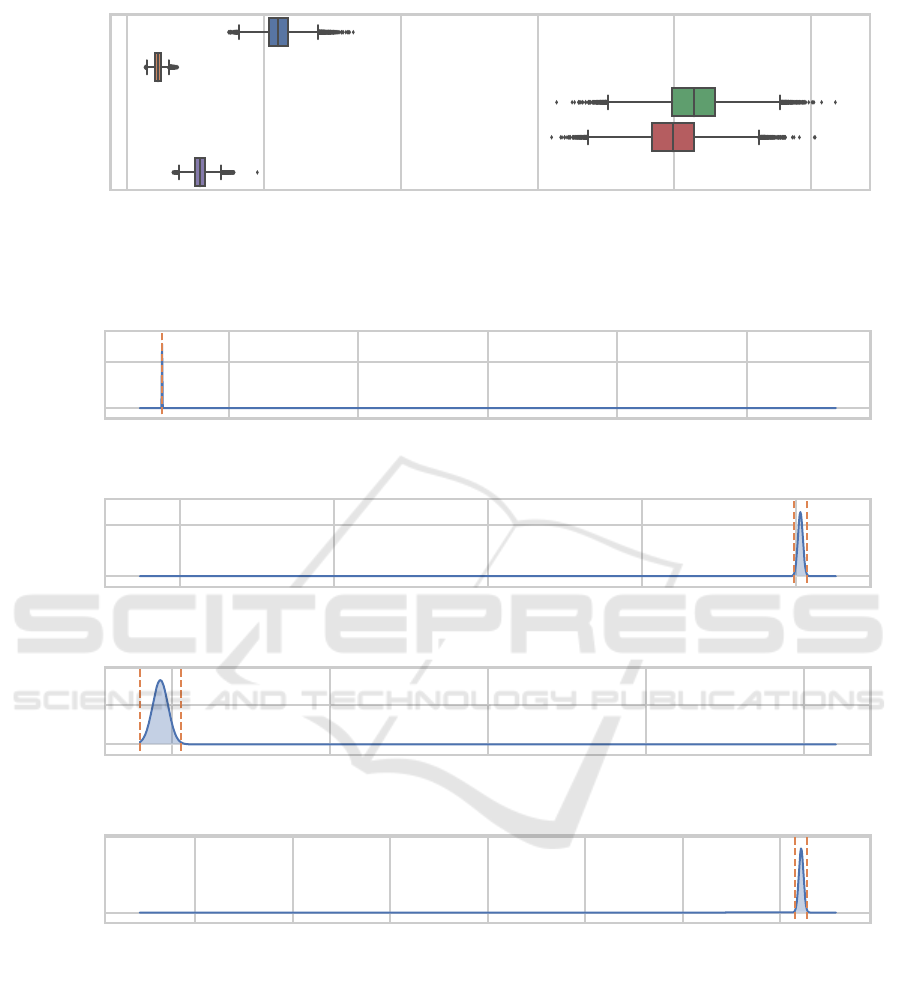
When considering model complexity (Figure 3),

there is an 80 % probability that one of NS and MCNS

performs the best. However, since the probability of

each of these not performing the best MSE-wise is

around 80 % or more, we do not consider them to be

ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications

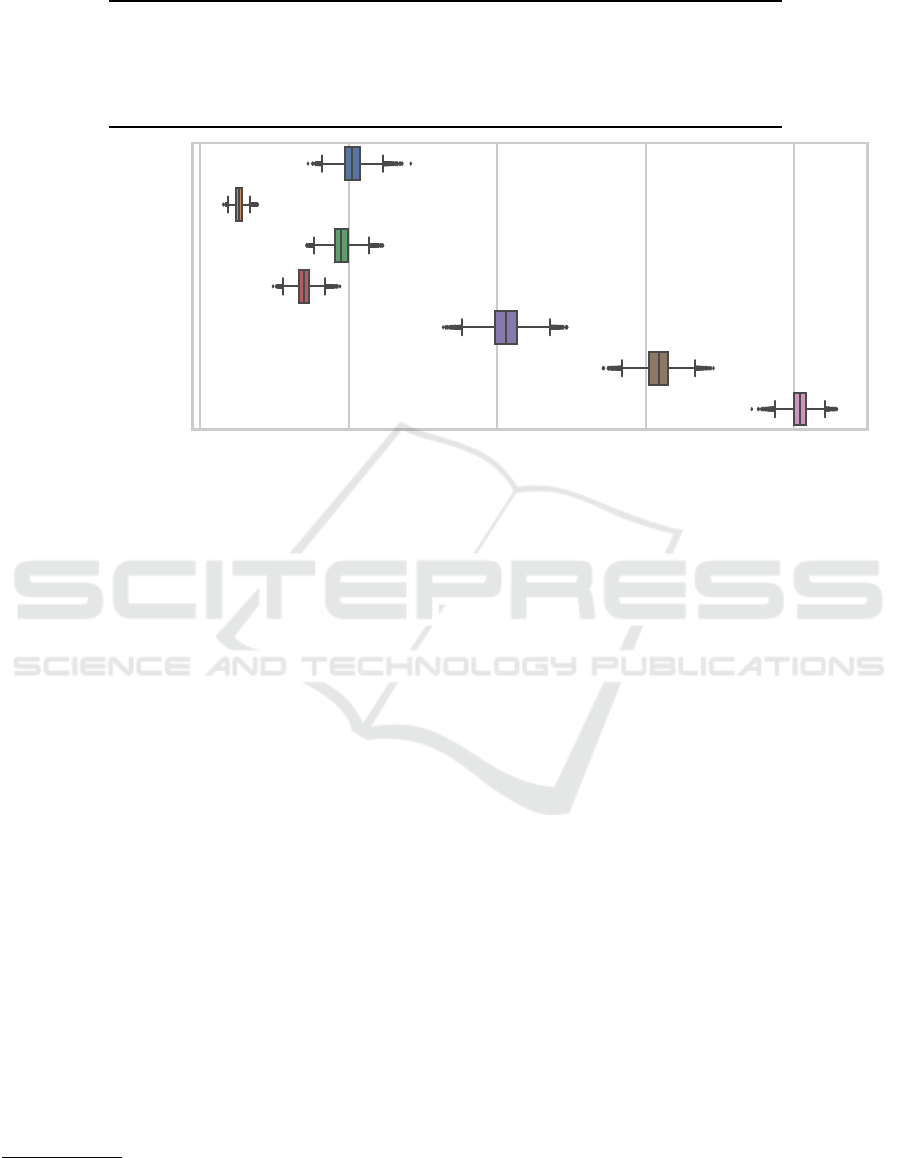
Table 3: Mean and standard deviation like Table 2 but for model complexity.

ES RS NS MCNS NSLC

CCPP 04.52 ± 1.48 12.86 ± 3.13 05.84 ± 0.91 06.02 ± 1.39 06.94 ± 1.41

ASN 31.78 ± 2.21 32.98 ± 3.11 18.22 ± 2.91 18.81 ± 2.46 29.75 ± 3.84

CS 24.95 ± 2.45 29.56 ± 2.47 23.50 ± 3.47 22.38 ± 3.02 33.83 ± 3.28

EEC 12.94 ± 2.10 30.17 ± 3.78 06.92 ± 1.70 06.22 ± 1.13 10.16 ± 1.94

0.0 0.2 0.4 0.6 0.8

Probability

MCNS

NSLC

ES ∧ NSLC

ES ∧ NSLC ∧ NS

RD method

Figure 2: Box plot (with standard 1.5 IQR whiskers and outliers) of the posterior distribution obtained from the model by

Calvo et al. (Calvo et al., 2018; Calvo et al., 2019) applied to the MSE data. An RD method having a probability value of q %

says that the probability of that RD method performing the best with respect to MSE is q %. In addition to each individual

RD method we also included the distributions for “either of ES or NSLC (or NS) perform best”.

competitive enough to merit a closer analysis within

the present work.

We next consider the difference in performance

between ES (since it is both the originally-used RD

method as well as the runner-up with respect to

the probability of being the best MSE-wise) and

NSLC (since it has the highest probability of hav-

ing the lowest MSE) by applying Corani and Be-

navoli’s Bayesian correlated t-test (Corani and Be-

navoli, 2015). The resulting posteriors (given in Fig-

ures 4 and 5 including 99 % HDIs) are the distribution

of the difference between the considered metric for

NSLC and the considered metric for ES (which means

that values larger than zero indicate NSLC having a

higher (worse) metric value than ES). It can be seen

that, on the CCPP dataset, the difference in MSEs be-

tween NSLC and ES is most certainly negligible in

practice which corroborates the earlier statement that

on that dataset all but RS perform similarly. On ASN,

on the other hand, ES outperforms NSLC by an MSE

of at least 0.04 with a probability of over 99 %

(99 %

of probability mass already lies between the dashed

lines alone and even more to the right the upper HDI

bound). The probability of NSLC outperforming ES

This means that in over 99 % of future runs we would

expect the MSE difference between the two approaches to

be at least 0.04.

on the CS dataset by an MSE of 0.019 to 0.022 is

99 %. On EEC, the last of the four datasets, there

is, again, not really a signiﬁcant difference to be no-

ticed (e.g. if a difference in MSE of 0.0033 could be

considered not practically relevant on this dataset then

the two should be considered to perform equivalently

with a probability of over 99 %).

Things look differently when regarding the model

complexities produced by the two approaches (Fig-

ure 5). On each of the datasets, there is considerable

probability mass on each side of 0. While we could

simply compute the integral to the left (or right) of 0,

this would include differences that are not relevant in

practice. We thus decided to deﬁne a region of prac-

tical equivalence (rope) centered on a complexity dif-

ference of 0. Since the learning tasks are very dif-

ferent in their model complexity (i.e. require different

solution sizes), we opted for a task-dependent rope.

As this is difﬁcult to choose based on the task alone

(i.e. requiring detailed domain knowledge about the

different processes that generated the data), we let the

collected data inform our choice of the rope for each

task: We choose as the bounds of the rope the mean of

the standard deviations of ES, NS, MCNS and NSLC

(leaving out RS since that method does not even re-

motely achieve competitive results with respect to so-

lution complexity). The rope for each task is included

Approaches for Rule Discovery in a Learning Classiﬁer System

0.0 0.1 0.2 0.3 0.4 0.5

Probability

MCNS

NSLC

RD method

Figure 3: Box plot like Figure 2 but for the model complexity metric.

−0.002 −0.001 0.000 0.001 0.002

50000

-0.0025-0.0025

CCPP

−0.04 −0.02 0.00 0.02 0.04

1000

0.04 0.041

ASN

−0.02 −0.01 0.00 0.01 0.02

500

-0.022 -0.019

−0.003 −0.002 −0.001 0.000 0.001 0.002 0.003

MSE(NSLC) - MSE(ES)

20000

Density

0.0032 0.0033

EEC

Figure 4: Density plot of the posterior distribution obtained from Corani and Benavoli’s Bayesian correlated t-test (Corani

and Benavoli, 2015) applied to the difference in MSE between NSLC and ES. Orange dashed lines and numbers indicate the

99 % HDI (i.e. 99 % of probability mass lies within these bounds). HDI bounds rounded to two signiﬁcant ﬁgures.

in Figure 5 as a green area delimited by green dotted

lines. Based on the rope and the Bayesian correlated

t-test model we can now compute the probabilities for

ES and NSLC performing practically equivalently or

worse than the other; they are given in Table 4. Upon

close inspection we can determine that for ASN, the

data is not conclusive. For CCPP and CS, ES pro-

duces less complex solutions than NSLC with a prob-

ability of 75.1 % and 86.2 % respectively. For EEC

there is some evidence hinting towards NSLC creat-

ing more compact solutions, however, this, again is

not fully conclusive as the probability of this not be-

ing the case is 34.4 %.

We conclude our analysis with a summary of the

key takeaways.

ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications

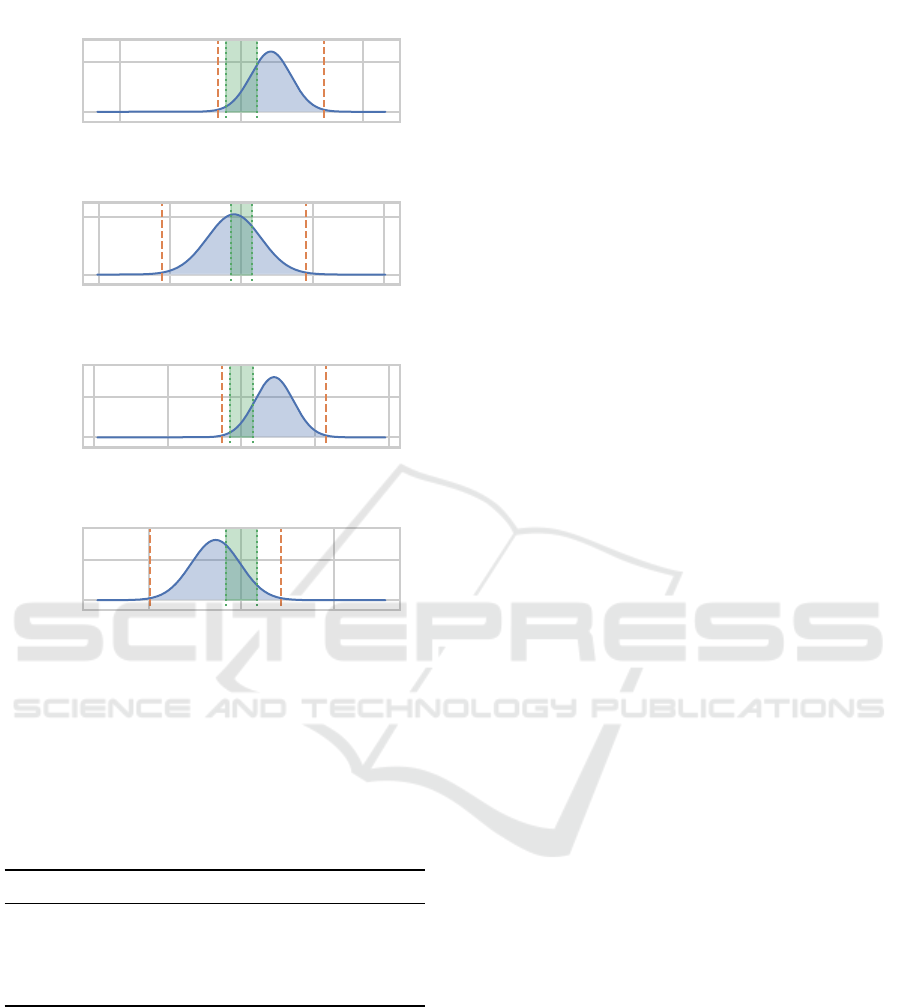
−10 0 10

0.0

0.2

-2.0 6.8

CCPP

−40 −20 0 20 40

0.00

0.05

-22.0 18.0

ASN

−40 −20 0 20 40

0.00

0.05

-5.1 23.0

−10 0 10

Model complexity(NSLC)

- Model complexity(ES)

0.0

0.1

Density

-9.9 4.3

EEC

Figure 5: Density plot like Figure 4 but for the model com-

plexity metric and with the region of practical equivalence

(rope) marked by green dotted lines and a green area.

Table 4: Probability (in percent, rounded to one decimal

place) of ES or NSLC performing better or worse than the

other—or practically equivalently—with respect to model

complexity.

ES worse pract. equiv. NSLC worse

CCPP 1.3 23.5 75.1

ASN 45.6 28.4 26.0

CS 1.4 12.4 86.2

EEC 65.6 29.6 4.9

• NSLC has the highest probability of being the

best option MSE-wise on datasets like the ones

we considered. However, the data we collected is

not entirely conclusive with respect to that (there

is still an around 60 % chance of NSLC not having

the best MSE on such datasets).

• When considering model complexity alone, there

is a high probability of either of NS or MCNS

being the best—however, their MSEs are with a

high probability not the best.

• A closer comparison of ES with NSLC yielded:

– ES outperforms NSLC MSE-wise with very

high probability (> 99 %) by a presumably

practically relevant amount on ASN whereas

this is the other way around on CS. However,

on these two tasks, the data is either not con-

clusive as to which method yields the better

model complexities (ASN) or the method with

the worse MSE performs better in that regard

(CS).

– On the other two tasks, ES and NSLC per-

form somewhat equivalently MSE-wise. There

is some light evidence for ES yielding better

model complexities on the less difﬁcult of these

(CCPP) and for NSLC yielding better model

complexities on the more difﬁcult one (EEC).

• Overall, we can say that despite its simplic-

ity when compared to the other approaches, the

(1,λ)-ES performs not worse when only consid-

ering practically relevant differences.

5 CONCLUSION

This work investigated the use of different evolution-

ary approaches towards rule discovery in the Super-

vised Rule-based learning system (SupRB), a recently

proposed Learning Classiﬁer System (LCS) for re-

gression problems. This system’s key characteristic

is the separation of ﬁnding a diverse pool of rules that

ﬁt the data well from their composition into a model

that is both accurate and uses a minimal number of

rules—a key advantage when employed in settings

where model transparency is important, such as typi-

cal explainable artiﬁcial intelligence applications. By

determining from intermediate solutions which areas

of the problem space were already well covered, sub-

sequent evolution can be guided towards other areas

to form new rules there and, therefore, improve the

overall diversity of the available rules.

The investigated methods were a (1,λ)-ES, a Ran-

dom Search (RS) and three Novelty Search (NS) vari-

ants. The NS-based variants all employed a (µ,λ)-

ES, scored a rule’s novelty on the basis of its match

set and combined it with traditional ﬁtness. Besides a

traditional NS, we investigated Minimal Criteria Nov-

elty Search (MCNS) and Novelty Search with Local

Competition (NSLC).

After an evaluation of the ﬁve methods on four

real-world regression problems, we found that perfor-

mances are similar but, depending on the dataset, spe-

ciﬁc methods can be preferred, with ES and NSLC

Approaches for Rule Discovery in a Learning Classiﬁer System

being the most interesting candidates. This was con-

ﬁrmed by a rigorous statistical analysis. Interestingly,

we found that where ES can be expected to perform

better on error than NSLC, it can also be expected to

yield larger solution sizes (a higher number of rules

in the model) and vice versa.

Overall, we recommend to use either ES or NSLC,

although, due to its greater simplicity and the fact that

rules are selected independently of the status of other

rules, ES seems to be the preferential candidate for

cases where model construction is important for the

explainability requirements of users.

ACKNOWLEDGEMENTS

This work was partially funded by the Bavarian Min-

istry of Economic Affairs, Energy and Technology.

REFERENCES

Akiba, T., Sano, S., Yanase, T., Ohta, T., and Koyama,

M. (2019). Optuna: A Next-generation Hyperpa-

rameter Optimization Framework. In Proceedings

of the 25th ACM SIGKDD International Conference

on Knowledge Discovery & Data Mining, KDD ’19,

pages 2623–2631, New York, NY, USA. Association

for Computing Machinery.

Benavoli, A., Corani, G., Dem

sar, J., and Zaffalon, M.

(2017). Time for a change: A tutorial for compar-

ing multiple classiﬁers through bayesian analysis. J.

Mach. Learn. Res., 18(1):2653–2688.

Brooks, T., Pope, D., and Marcolini, M. (1989). Airfoil

Self-Noise and Prediction. Technical Report RP-1218,

NASA.

Calvo, B., Ceberio, J., and Lozano, J. A. (2018). Bayesian

inference for algorithm ranking analysis. In Proceed-

ings of the Genetic and Evolutionary Computation

Conference Companion, GECCO ’18, pages 324–325,

New York, NY, USA. Association for Computing Ma-

chinery.

Calvo, B., Shir, O. M., Ceberio, J., Doerr, C., Wang, H.,

ack, T., and Lozano, J. A. (2019). Bayesian per-

formance analysis for black-box optimization bench-

marking. In Proceedings of the Genetic and

Evolutionary Computation Conference Companion,

GECCO ’19, pages 1789–1797, New York, NY, USA.

Association for Computing Machinery.

Corani, G. and Benavoli, A. (2015). A bayesian approach

for comparing cross-validated algorithms on multiple

data sets. Machine Learning, 100(2):285–304.

Dua, D. and Graff, C. (2017). UCI machine learning repos-

itory. http://archive.ics.uci.edu/ml.

Gomes, J., Mariano, P., and Christensen, A. L. (2015). De-

vising effective novelty search algorithms: A com-

prehensive empirical study. In Proceedings of the

2015 Annual Conference on Genetic and Evolution-

ary Computation, GECCO ’15, page 943–950, New

York, NY, USA. Association for Computing Machin-

ery.

Gomes, J., Urbano, P., and Christensen, A. L. (2012). Pro-

gressive minimal criteria novelty search. In Pav

on,

J., Duque-M

endez, N. D., and Fuentes-Fern

andez,

R., editors, Advances in Artiﬁcial Intelligence – IB-

ERAMIA 2012, pages 281–290. Springer Berlin Hei-

delberg.

Heider, M., Nordsieck, R., and H

ahner, J. (2021). Learn-

ing Classiﬁer Systems for Self-Explaining Socio-

Technical-Systems. In Stein, A., Tomforde, S., Botev,

J., and Lewis, P., editors, Proceedings of LIFELIKE

2021 co-located with 2021 Conference on Artiﬁcial

Life (ALIFE 2021).

Heider, M., Stegherr, H., Nordsieck, R., and H

ahner,

J. (2022a). Learning classiﬁer systems for self-

explaining socio-technical-systems. https://arxiv.org/

abs/2207.02300. Submitted as an extended version of

(Heider et al., 2021).

Heider, M., Stegherr, H., Wurth, J., Sraj, R., and H

ahner, J.

(2022b). Separating Rule Discovery and Global So-

lution Composition in a Learning Classiﬁer System.

In Genetic and Evolutionary Computation Conference

Companion (GECCO ’22 Companion).

Heider, M., Stegherr, H., Wurth, J., Sraj, R., and H

ahner, J.

(2022c). Investigating the impact of independent rule

ﬁtnesses in a learning classiﬁer system. http://arxiv.

org/abs/2207.05582. Accepted for publication in the

Proceedings of BIOMA’22.

Kaya, H. and T

ufekci, P. (2012). Local and Global Learn-

ing Methods for Predicting Power of a Combined Gas

& Steam Turbine. In Proceedings of the Interna-

tional Conference on Emerging Trends in Computer

and Electronics Engineering ICETCEE.

Lehman, J. (2012). Evolution Through the Search for Nov-

elty. PhD thesis, University of Central Florida.

Lehman, J. and Stanley, K. O. (2010). Revising the evo-

lutionary computation abstraction: Minimal criteria

novelty search. In Proceedings of the 12th Annual

Conference on Genetic and Evolutionary Computa-

tion, GECCO ’10, page 103–110, New York, NY,

USA. Association for Computing Machinery.

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,

Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P.,

Weiss, R., Dubourg, V., Vanderplas, J., Passos, A.,

Cournapeau, D., Brucher, M., Perrot, M., and Duch-

esnay,

E. (2011). Scikit-learn: Machine Learning in

Python. The Journal of Machine Learning Research,

12:2825–2830.

Tsanas, A. and Xifara, A. (2012). Accurate Quantitative Es-

timation of Energy Performance of Residential Build-

ings Using Statistical Machine Learning Tools. En-

ergy and Buildings, 49:560–567.

ufekci, P. (2014). Prediction of full load electrical power

output of a base load operated combined cycle power

plant using machine learning methods. Interna-

tional Journal of Electrical Power & Energy Systems,

60:126–140.

ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications

Urbanowicz, R. J. and Browne, W. N. (2017). Introduction

to Learning Classiﬁer Systems. Springer Publishing

Company, Incorporated, 1st edition.

Urbanowicz, R. J. and Moore, J. H. (2009). Learning Clas-

siﬁer Systems: A Complete Introduction, Review, and

Roadmap. Journal of Artiﬁcial Evolution and Appli-

cations.

Wilson, S. W. (1995). Classiﬁer ﬁtness based on accuracy.

Evolutionary Computation, 3(2):149–175.

Wurth, J., Heider, M., Stegherr, H., Sraj, R., and H

ahner, J.

(2022). Comparing different metaheuristics for model

selection in a supervised learning classiﬁer system.

In Genetic and Evolutionary Computation Conference

Companion (GECCO ’22 Companion).

Yeh, I.-C. (1998). Modeling of Strength of High-

Performance Concrete Using Artiﬁcial Neural Net-

works. Cement and Concrete Research, 28(12):1797–

1808.

Approaches for Rule Discovery in a Learning Classiﬁer System