On the Impossibility to Assure a Finite Software Concepts’ Catalog

Iaakov Exman

Software Engineering Dept., The Jerusalem College of Engineering - Azrieli, Jerusalem, Israel

Keywords: Knowledge Discovery, Concepts, Natural Language, Conceptual Integrity, Software Concepts’ Catalog,

Software Systems Theory.

Abstract: In recent times it has been recognized that Concepts play a central role within Software. This has been

expressed by Fred Brooks’ idea that “Conceptual Integrity is the most important consideration for software

system design”. However, concepts as human natural language words with assigned meaning by the Concepts’

relationships, evolve under continual dynamics of concepts discovery. This language dynamics has

consequences that cannot be ignored. This paper illustrates concepts discovery within design patterns, up to

very large-scale systems, highlighting intrinsic shortcomings of Concepts’ semantics as a solid basis for

Software Conceptual Integrity. Paradoxically, these shortcomings are the consequence of the very creative

process of Concepts Discovery from existing knowledge. Finally, one arrives at the paper’s main results: the

absolute Software Concepts freedom of choice, typical of natural languages, implies the impossibility to

assure a finite Software Concepts catalog. One finds oneself in an unending pursue of additional concepts to

achieve some kind of Integrity or completeness. Even deliberate finite catalogs cannot be definitive. But there

is no reason for despair. Finite Software Concepts’ catalogs, despite not definitive, are still very useful.

1 INTRODUCTION

The language of software design is any human natural

language, whose aim is to be understood by humans,

and eventually by Artificially Intelligent robots.

What tells apart the natural language of software

system design from lower levels of programming

languages? The latter usually have restricted and

static numbers of reserved words and syntax, whose

goal is to be actuators of computing machines.

Human live languages, in continual dynamics,

create new words, change and add word meanings,

and turn obsolete other words. This absolute

Concepts’ invention freedom, and naturally evolving

thesaurus, are a software design bonus, but incurs

limitations, the goal of this paper’s investigation.

1.1 Concepts’ Semantics are Part of the

Software Essence

Concepts are words of a human natural language, e.g.,

English, Mandarin Chinese, or Portuguese, with

assigned meaning by the Concepts’ relationships,

which are composable into software concept systems.

https://orcid.org/0000-0002-9917-3950

What are fundamental software concepts’ system

properties? Concepts’ semantics are part of the

software essence. But this is not the whole story.

Brooks’ Conceptual Integrity thought as “the

most important consideration for software system

design”, can be implemented from his principles

(Brooks, 2010): propriety – a software system should

have only concepts essential to its purpose and no

more; orthogonality – software system concepts

should be totally independent of one another.

1.2 Concept Discovery as Software

Liveness

Software system design liveness consists in

everlasting concepts discovery/invention, and

creation or modification of concepts relationships.

Concepts discovery refers to mutual concepts

adjustment to achieve Conceptual Integrity for a

given software system.

It also refers to variations of an original system

into a slightly different system. For instance, different

but similar car models have much in common, one for

Exman, I.

On the Impossibility to Assure a Finite Software Concepts’ Catalog.

DOI: 10.5220/0011553400003335

In Proceedings of the 14th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2022) - Volume 1: KDIR, pages 273-280

ISBN: 978-989-758-614-9; ISSN: 2184-3228

273

regular family usage, and another station-wagon

model, with larger space for luggage.

1.3 Paper’s Focus and Organization

This paper focuses on the Concept discovery extreme

dynamics of natural languages, and how it affects

software semantics.

Section 2 illustrates software design pattern

concepts discovery. Section 3 deals with very large-

scale concepts’ systems. The main theoretical results

are formulated in section 4, the finite and definitive

concepts catalog impossibility theorems. The paper is

concluded with Related Work in Section 5, and a

Discussion in Section 6.

2 SOFTWARE DESIGN PATTERN

CONCEPTS DISCOVERY

Design Patterns are frequently used small software

sub-systems, defined in terms of natural language

concepts, whose purpose is to compose software

systems at the design level.

2.1 Software Design Patterns

Design Patterns are relevant to this paper since they

are abstractions of the small sub-systems they

represent. They are reusable by substituting the

abstractions by actual concepts of the specific

application being built.

The software composition design process is

creative in two senses. One sense is planning an

overall software architecture. The other is naming

specific structures and functions. The concept

discovery naming activity is done either by choice of

existing or modified suitable concepts, or by

inventing new words and/or meanings.

The two design patterns analysed in this section,

illustrate and explain the nature of the concept

discovery process. They were taken from the well-

known Design Patterns GoF book. GoF means “Gang

of Four”, a humorous reference to its four authors

(Gamma et al., 1995).

2.2 The Composite Pattern

Composite is a design pattern – (Gamma et al., 1995)

page 163 – which composes objects into tree graphs

representing part-whole hierarchies. Individual

objects and their composites are treated uniformly

with respect to certain specific operations.

The abstract concepts of the Composite design

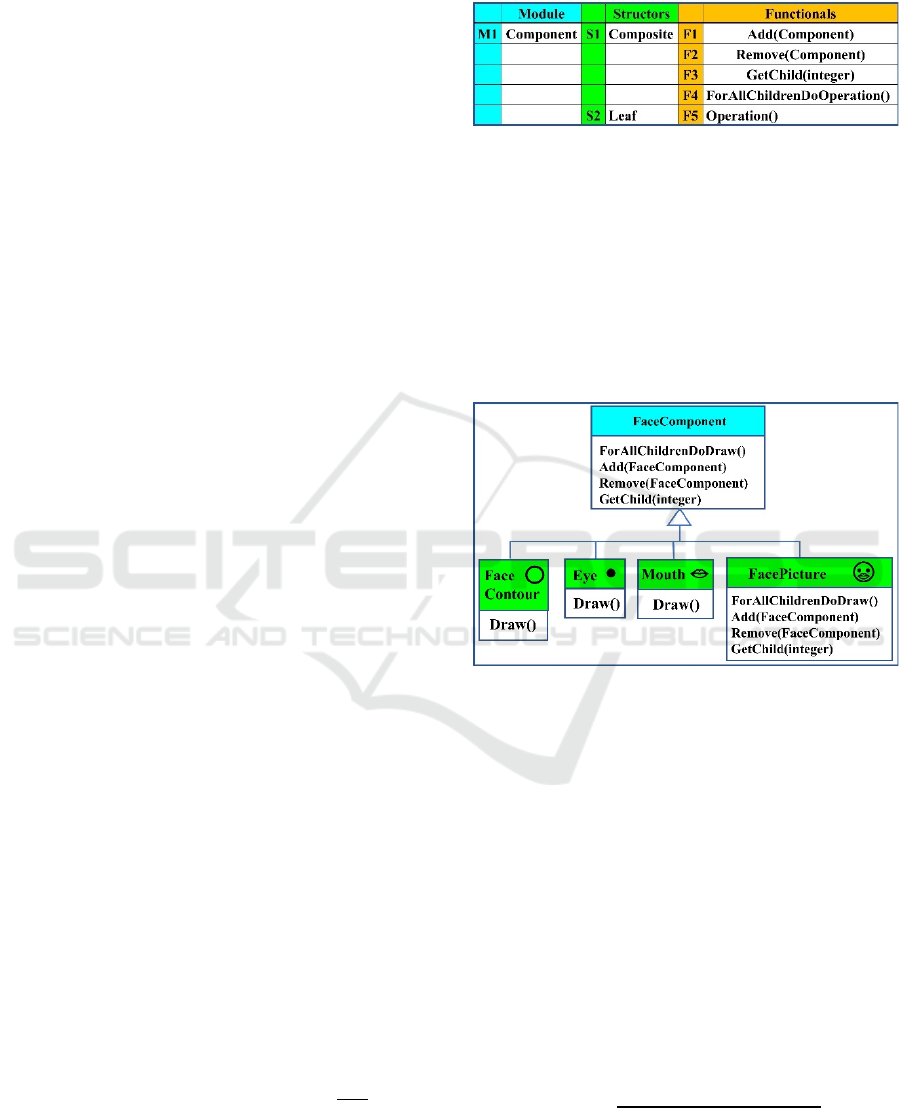
pattern are shown in Fig. 1.

Figure 1: Composite Design Pattern: Abstract Concepts –

This pattern is a single Module, whose building blocks are

Components. It contains 2 structure types: A composite and

a leaf. A composite may add/remove components, or get a

child name. Specific operations can be done on any

composite child or on a leaf. (Figures in color online).

A specific example of the Composite Design

Pattern is the FaceComponent shown in Fig. 2. This

is just one application example of the abstract Design

Pattern. Many different applications are possible.

Figure 2: Composite Design Pattern: FaceComponent – It

has 3 “leaves” (Face Contour, Eye and Mouth), and 1

Composite, the FacePicture, composed of 4 children (a Face

Contour circle, one mouth and 2 eyes). The vertical arrow

with a triangle arrowhead means that the 3 leaves and the

Composite inherit FaceComponent functions. Draw is the

specific operation of this Design Pattern. This figure is an

inverted tree with a top root and 3 leaves at the bottom.

This design pattern special idea is that individual

leaves and composites are components, treated in the

same way: one can add any component to an existing

composite. A composite’s children can be leaves and

internal composites. A leaf cannot have children.

The Draw function of the leaves is the same as the

generic composite function ForAllChildrenDoDraw,

assuming the number of children of a leaf to be zero.

A few notes analysing this pattern concepts are:

 Concepts are natural language words – (Face,

Eye, Mouth, Child, Leaf, Draw, Composite, Add,

Remove). But one readily perceives that these are

metaphors: a face in Fig. 2 is not a realistic face.

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

274

 Necessarily the system is incomplete – one can

easily add concepts absent in this example

(moustache, ears, nose, hair, shadows, etc.).

 New concepts are continually created – language

dynamics causes relevant concepts discovery or

invention, e.g., by technology advances.

Some recent examples of newly created concepts

are emoticon – short for "emotion icon", text-based

symbols such as :-) replacing language – and emoji –

a word of Japanese origin with ‘e’ meaning ‘picture’

and ‘moji’ meaning ‘character’ – used for facial

expressions, and to reveal emotions.

2.3 The Observer Pattern

Observer is a design pattern – (Gamma et al., 1995)

page 293 – that formally defines a one-to-many

dependency between objects: when one is changed,

all the others are notified and updated. The abstract

concepts of the Observer design pattern are in Fig. 3.

Figure 3: Observer Design Pattern: Abstract Concepts –

The Observer Pattern is a single Module. It contains two

types of structures: A subject and an observer. A subject

attaches/detaches observers, notify observers that it has

changed, and enables setting/getting its state. Any observer

updates its state according to the current subject state.

A concrete example of the Observer Design Pattern is

a school with different floors, and many classrooms,

each of them with a wall-clock. If a seasons’

transition occurs, from wintertime to summertime for

daylight saving, one has to adjust all classroom clocks

one-by-one. With a central clock linked to all other

school clocks, it would be enough to adjust only the

central clock, as shown in Fig. 4.

Figure 4: Observer Design Pattern: A system of clocks –

The central clock is the subject (of Fig. 3) and the classroom

clocks are the observers. The central clock notifies all the

classroom clocks, which get the Central Clock state and

each one of the classroom clocks updates itself.

The analysis of the Observer Design pattern is

similar to the Composite pattern:

 Concepts are natural language words – (clock,

central, classroom, notify, attach, detach, state,

update).

 Necessarily the system is incomplete – many

possible concepts can be added to such a system

(digital vs. analog clocks, season, summertime,

time-zone, etc.).

 New concepts are continually created – language

dynamics together with technology advances

cause concepts discovery or invention.

Some recent examples of new concepts are UTC

– Coordinated Universal Time, a standard reference

to the British Greenwich Mean Time (GMT), serving

as the offset basis for time-zones – atomic clocks

made of Cesium, the most precise clocks, certainly

not necessary in a secondary school – GPS – Global

Positioning System – a global satellite system, also a

precise source of time and location. A very popular

application for everyday life is a handheld GPS watch

used as a bracelet for sports and fitness. A GPS watch

may also be a smartwatch.

3 VERY LARGE-SCALE SYSTEM

CONCEPTS DISCOVERY

Here we jump up from small-scale modules to Very

Large-Scale Systems, examining concepts discovery.

We begin displaying empirical data on the

significant increase of vocabulary of natural

languages. Then we deal with examples of

astronomic objects and electronic VLSI (Very Large

Scale Integrated) circuits.

3.1 Empirical Data and Graph

A representative snapshot of the dynamics of natural

language is given by data about the English language,

from a paper which analysed a huge quantity of

digitized books (Michel et al., 2011).

The referred paper’s estimate of the number of

words in the English vocabulary along the time axis

is: 544 kilowords in the year 1900, 597 kilowords in

1950 and 1022 kilowords in the year 2000.

These data are shown in Fig. 5. One clearly

perceives an acceleration of the net increase of words

along the years 1950 to 2000.

The referred paper

estimated the English net increase rate of number of

words, eliminating obsolete word spelling and usage,

from 1950 to 2000, as about 8500 words per year.

On the Impossibility to Assure a Finite Software Concepts’ Catalog

275

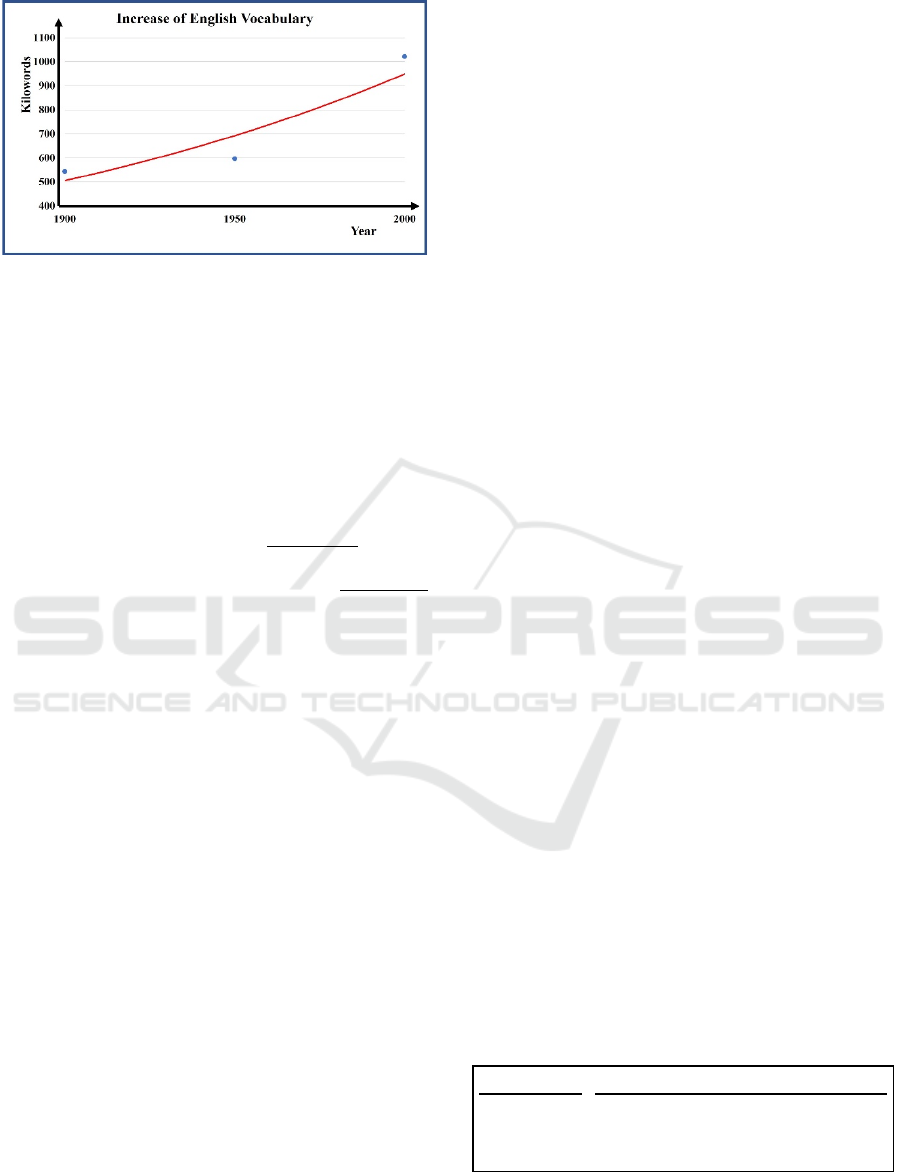
Figure 5: Number of kilowords in the English vocabulary

along the years (blue dots) and exponential trendline (red).

We have mentioned creative mechanisms causing

natural language vocabulary increase, in section 2.

These mechanisms include technological advances

due to deep scientific theories – e.g., GPS needs

relativistic corrections – mixed with everyday life

activities such as sports and states of mind like

emotions.

In the next sub-sections, we encounter somewhat

different motivations for concepts discovery:

 to make more familiar very large natural

phenomena – stars and galaxies;

 to make sense of a multitude of very small

components, human made by nanotechnologies.

3.2 Astronomical Objects

Referring to astronomical objects in the Universe, one

should pay attention to two facts.

fact, the estimated number of astronomical

objects is huge. For instance, the estimated number of

galaxies in the Universe is between 2 trillion – e.g.

(Conselice, 2016) – and the more recent and modest

number of 200 billion. The estimated number of stars

per galaxy ranges from a few hundred million (10

)

stars to one hundred trillion (10

) stars. Multiplying

the number of galaxies by the number of stars one gets

by any estimate a giant number.

fact, despite the huge numbers, human beings

throughout the History discovered/invented names

and assigned meanings to astronomical objects:

galaxies, stars, constellations, planets, lunar craters,

asteroids, and whatever; to organize knowledge, and

to make sense of the huge Universe for humans.

The milk root of the word “galaxy” and the name

of our own galaxy the “milky way” (Licquia, 2015) is

due to a perceived white smear in the night sky.

Constellation names are suggestive of ideas and

patterns recognized by humans, among them the

southern cross, appearing in the Australian, Brazilian

and New Zealand flags, which had a navigation role

in the southern hemisphere of planet Earth.

Zodiac, a very old notion – derived from the

Greek zoidion, “little animal” – is due to

constellations visualized as little animals. It is a belt-

shaped region of the sky that extends north or south

of the ecliptic – the plane of the orbit of the Earth

around the Sun. The zodiac concept is still used in

modern astronomy – see e.g., (Licquia, 2015), and

sub-section 5.5 of Related Work.

3.3 VLSI Objects

VLSI (Very Large Scale Integrated) circuits have

electronic components with a huge number of

transistors packed in a single chip. The current

(March 2022), system on a chip transistor count is of

the order of 114 billion transistors, as announced in a

consumer electronics press release (M1-Ultra, 2022).

Transistors’ count has a surprising quantitative

similarity to galaxies. The transistors count in a chip

is of the same order of magnitude of the galaxies

number in the Universe.

Is this a real surprise? Or is it an expected

consequence of the same scientific and engineering,

ideas and tools, being used by humans, despite so

different knowledge fields?

Digital electronic chips, with concepts as – logic

gates, capacitors, memory units – are nowadays

designed with software tools in which these concepts’

semantics play an essential role.

4 FINITE CONCEPTS CATALOG

IMPOSSIBILITY

This section states this paper’s theoretical results.

After some preliminary definitions, we summarize

the theorems motivation, then formulate and prove

the theorems.

4.1 Preliminary Definitions

The definitions are needed for the theorem statement.

Each definition depends on the preceding one.

Definition 1: Natural Language Word Meaning.

Meaning is assigned as a set of natural language

words, a set with at least one word, not including

the word whose meaning is being assigned.

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

276

4.2 Theorems Motivation

The language of software is any human natural

language, constantly changing its vocabulary. This

occurs by adding words, deleting obsolete words, or

changing words meanings.

The natural languages’ concept extraordinary

dynamics is the theorems’ foundational assumption.

We see no reason for language dynamics weakening

in a foreseeable future.

4.3 Finite Catalog Impossibility

Theorem

The first theorem is in the textbox below:

Proof:

The proof idea is by construction. One obtains an

infinite Software Concepts’ System catalog, through

an infinite recursion of assigned meanings to words.

The words used in this proof are natural number

names in a chosen language. In English these would

be: zero, one, two, three, four, …, etc. Every natural

number in any natural language has its own specific

name, despite the infinite set of natural numbers.

By assumption (a) there is absolute freedom of

words choice and their respective assigned meanings.

We assign to each natural number as its meaning “any

of the successors of the current or the following

natural numbers”. For instance, the successor(three)

= four, and the successor(four) = five.

By assumption (b) meanings are transitive thus

the successors of three are four, and five, and so on.

By induction, any natural number has an infinite

number of successors.

There is no impediment to include natural

numbers in any Software Concepts’ System, thus it is

impossible to assure that a catalog remains finite. ⧠

Some comments on the Finite Concepts’ Catalog

Impossibility theorem are:

 The justification for the choice of the meanings of

the natural numbers is the Axioms of Peano. Thus,

the meaning of each natural number is given by

the whole set of Peano Axioms.

 We choose zero as the 1

natural number for

compatibility with the Peano Axioms.

 A transitivity example is: the result meaning is

assigned to consequence; the consequence

meaning is assigned to outcome; by transitivity

the result meaning is also outcome.

 Meaning is transitive, but it is not symmetric.

4.4 Definitive Catalog Impossibility

Theorem

We again need a preliminary definition:

Intuitively, the impossibility to assure definitive

Software Concepts’ Systems catalogs is even more

plausible than the impossibility to assure finite

catalogs. This is also due to natural language

dynamics – whether the system is finite or infinite –

as was argued in several ways in this paper’s sections.

The next theorem formalizes this intuition.

Definition 2: Software Concept System. Software

concept system at the design level is defined by its

concepts, which are natural language words with

their meanings.

Definition 3: Software Concept System Catalog. A

catalog is an organized structure of software

concepts’ system definitions, with explicitly stated,

not necessarily linear, organizing criteria.

Theorem 1: Finite Concepts’ Catalog

Impossibility

Assuming – the three preliminary definitions

and the two following assumptions:

a) Absolute freedom of meaning choice – natural

language freedom refers to the word whose meaning

is assigned and to the word set assigned as meaning;

a single word may have an unrestricted number of

assigned meanings.

b) Meaning is a transitive relation – The meaning

of a meaning of a word is also a meaning of the

original word.

Then –

It is impossible to assure that a Software Concepts’

Systems Catalog remains finite.

Definition 4: Definitive Catalog. A software

concepts’ systems catalog is definitive, if after

reaching a stable definition of all its software

concepts’ systems, as decided by their inventors, it

will not change anymore.

Theorem 2: Definitive Concepts’ Catalog

Impossibility

Assuming –

a) Theorem 1 – its assumptions and its conclusion,

viz. the impossibility to assure that a Software

Concepts’ Systems Catalog remains finite.

Then –

It is impossible to assure that a Software Concepts’

Systems Catalog remains definitive.

On the Impossibility to Assure a Finite Software Concepts’ Catalog

277

Proof:

Even if one decides to limit the catalog size to an

arbitrarily chosen maximal integer, it is a trivial

corollary of Theorem 1 that such a catalog can be

extended as far as one wishes. Thus, the conclusion

of Theorem 2 is proven. ⧠

Some comments on the Definitive Concepts’ Catalog

Impossibility theorem are:

 The importance of Theorem 1 is to serve the proof

of Theorem 2.

 Finite catalogs are more important in practice than

infinite ones, even though both theorems have

significant implications (see section 6).

5 RELATED WORK

We have chosen a few deeper topics for a concise set

of references to relevant literature.

5.1 Conceptual Integrity

Conceptual Integrity is Frederick Brooks’ idea of the

most important consideration for software system

design, which at first sight is not so obvious. It has

been first proposed and developed in his two well-

known books: “The Mythical Man-Month” (Brooks,

1995) and “The Design of Design” (Brooks, 2010).

Brooks also offered principles to be followed in

order to attain Conceptual Integrity: propriety and

orthogonality. Various authors adopted Brooks’

Conceptual Integrity ideas.

It is remarkable that the Conceptual Integrity

constructive and convincing idea, solidified after a

previous rather pessimistic viewpoint published in

Brooks’ paper on “No Silver Bullet - Essence and

Accidents of Software Engineering” (Brooks, 1987).

It was disputed by David Harel in his reply paper

“Biting the Silver Bullet: Toward a Brighter Future of

System Development” (Harel, 1992).

5.2 Naming and Natural Numbers

Our Theorem 1 proof assumes that every natural

number in any natural language has its own specific

name, despite the infinite set of natural numbers.

A minimal symbol set to write the infinite natural

number names is {0, S}, zero and S i.e., Successor, in

the Peano Arithmetic (PA) language: 0, S0, SS0,

SSS0, …;

For instance, SS0 reads Successor(Successor(0))

is the number 2. In this notation the number of S

symbols tends to infinity. The paper (Horsten, 2005)

mentions PA language, and offers a framework to

investigate names canonicity and naming systems.

Shorter number names ask for word combinations

such as ‘one thousand three hundred’. This assumes

that a finite word set suffices to name infinite natural

numbers, with repeated use of the word set.

Different natural languages have semantically

different number names. For instance, 90 in English

is ‘ninety’ and in French it is ‘quatre-vingt-dix’

meaning “four times twenty plus ten”.

Referring to the Peano arithmetic axiomatization,

the mathematician Henri Poincare (Poincare, 1914)

claimed that arithmetic is a synthetic science whose

objects are not independent from human thought.

Naming in general, is a challenging philosophical

issue. It is discussed in a book “Naming, Necessity

and Natural Kinds” edited by Stephen Schwartz

(Schwartz, 1997), with chapters by several authors.

5.3 Infinite Catalogs

A paper by Allison-Cassin (Allison-Cassin, 2012)

referring to “The Possibility of the Infinite Library”

obviously demands infinite catalogs.

Allison-Cassin compares linear traditional library

catalogs, with the great expectations of the Internet

“infinite library”, with non-linear Hypertext links.

Concerning the term “bibliographic universe”

Allison-Cassin clearly highlights the problematics of

this universe, stressing that this “universe implies an

openness that is not fully accounted for by the idea of

totality”.

5.4 The Infinite Library of Babel

Nothing compares to literature in ideas expressivity,

such as infinity in a fascinating short story entitled

“The Library of Babel” by the fiction writer Jorge

Luis Borges (Borges, 1941).

The story tells us that “The Universe (which

others call the Library) is composed of an … infinite

number of hexagonal galleries”. As it continues “Like

all men of the Library, in my younger days … I have

journeyed in quest of a book, … the catalog of

catalogs.” Finally, one encounters “…thousands and

thousands of false catalogs, …, a proof of the falsity

of the true catalog…”

5.5 Catalogs of Virtually Unending

Stars

Many scientific papers describe how to estimate the

number of stars in the Milky Way and beyond. All

papers make inferences from star catalogs.

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

278

Licquia et al. (Licquia, 2015) present a new

statistical method to determine photometric

properties of the Milky Way, allowing our Galaxy to

be compared to objects found in extragalactic

surveys. It mentions and uses catalogs.

Astraatmadja and Bailer-Jones (Astraatmadja,

2016) inferred distances for two million stars using

parallaxes published in the Gaia DR1 catalog from

the European Space Agency.

Lauer et al. (Lauer, 2020) used images of NASA’s

New Horizons spacecraft cruising the most distant

solar planet Pluto to derive limits on the Cosmic

Optical Background (COB). Its basic insight is that

Universe formation and evolution comes from

knowing how dark the night sky is. COB is an integral

over the cosmological history of star formation

occurring in recognizable galaxies. Lauer’s paper

mentions the Gaia DR2 catalog, among others.

6 DISCUSSION

We discuss the importance of the Finite/Definitive

Impossibility Theorems. It is claimed that software

catalogs are not software theories, and one asks why

nonetheless they are useful. Finally, we state future

work and the main contribution of this paper.

6.1 Absolute Freedom of Meaning

Choice

The center of gravity of the Finite/Definitive

Impossibility Theorems is the natural language

assumption of Absolute freedom of meaning choice.

We took the liberty to represent any meaning

choice by the infinite set of integers – in fact the

Peano Axioms. This choice, rather than arbitrary, is

reasonable, since numbers are frequent participants of

software concept systems.

6.2 Importance of Finite/Definitive

Impossibility Theorems

If Concepts’ Catalog could be assured to be finite and

definitive, it would be a first step towards

formalization of software system Catalogs as theories

of Software as a whole, by themselves. But this would

sacrifice the assumption of Absolute freedom of

meaning choice.

Any organized concepts’ structure, analogous to a

catalog – e.g. taxonomy, dictionary, encyclopaedia –

is by itself neither a full-fledged software theory nor

a substitute for an autonomous agent evolving on its

own.

Concepts’ semantics are indeed an essential part

of software. Nevertheless, software theories should

have an algebraic theoretical component,

complementing the Conceptual aspect. But these

considerations are out of the scope of this paper, and

are dealt with elsewhere – see e.g., (Exman and

Sakhnini, 2018), (Exman and Wallach, 2020) and

(Exman and Shmilovitch, 2021).

6.3 The CYC Counterexample

A counterexample to Theorem 1 is Cyc, succinctly

described as an attempt to compose a finite catalog

about how the world works, doubtless a very

ambitious goal.

In neutral terms Cyc is a long-range Artificial

Intelligence (AI) project aiming at a comprehensive

ontology and knowledge base spanning concepts and

rules, to capture common sense knowledge.

It started in 1984 by Douglas Lenat (Lenat, 1990)

and still is under development. Its ontology, as of the

stable release of 2017, contains about 1,500,000 (one

million and a half) terms.

Criticism has stated the Cyc problems are

“unending amount of data required to produce any

viable results and the inability for Cyc to evolve on

its own”. The late Marvin Minsky, from the MIT AI

laboratory, said that "strategies most popular among

AI researchers in the 1980s reached a dead end."

6.4 Usefulness of Finite Catalogs

A widely known explicit finite catalog is the so-called

GoF book (Gamma et al., 1995) on software design

patterns. It contains 23 design patterns classified into

three categories: Creational, Structural and

Behavioral. It triggered publication of other catalogs,

on specific topics, such as Software Architecture

(Buschmann et al., 1996), Communications Software

(Rising, 2001), and Concurrent and Networked

Objects (Schmidt et al., 2000).

The GoF book was influenced by the architectural

book by Christopher Alexander (Alexander, 1977) on

pattern languages for towns and buildings.

The GoF patterns catalog is hard to formalize,

which is not unexpected according to the current

paper claims. Despite not being definitive, which fits

our Theorem 2, the GoF design patterns’ finite

catalog is useful and was influential, stimulating a

new way of thought about a higher abstraction level

of software design.

On the Impossibility to Assure a Finite Software Concepts’ Catalog

279

6.5 Future Work

There remain open issues of interest, deserving a

deeper investigation. An issue in need of a neat

resolution, is the apparent contradiction between:

a) Brooks’ propriety principle – a software system

should have only concepts essential to its purpose and

no more – apparently implying that software

concepts’ systems complying with Conceptual

Integrity should and can be finite;

b) Theorem 1 – which tells that it is impossible to

assure that a software concepts’ system catalog

remains finite.

6.6 Main Contribution

The main contributions of this paper are the

Impossibility Theorems to Assure a Finite and

Definitive Software Concepts’ Catalog. Nonetheless,

finite but not definitive catalogs can indeed be useful.

REFERENCES

Alexander, Christopher, (1977). a Pattern Language:

Towns/Buildings/Construction, Oxford University

Press, Oxford, Uk.

Allison-Cassin, Stacy, (2012). “the Possibility of the

Infinite Library: Exploring the Conceptual Boundaries

of Works and Texts of Bibliographic Description”,

Journal of Lib. Metadata, 12, Issue 2-3, Pp. 294-309,

Doi: Https://Doi.Org/10.1080/19386389.2012.700606.

Astraatmadja, Tri L., and Bailer-Jones, Coryn a.L., (2016).

“Estimating Distances from Parallaxes Iii. Distances of

Two Million Stars in the Gaia Dr1 Catalogue”,

Astrophysical Journal, 833:119. Doi: 10.3847/1538-

4357/833/1/119.

Borges, Jorge Luis, (1998). Collected Fictions, Penguin

Books, New York, Ny, Usa.

Brooks, Frederick P., (1987). “No Silver Bullet - Essence

and Accidents of Software Engineering”, IEEE

Computer, Vol. 20, No. 4, Pp. 10-19.

Brooks, Frederick P., (1995) the Mythical Man-Month –

Essays in Software Engineering – Anniversary Edition,

Addison-Wesley, Boston, Ma, Usa.

Brooks, Frederick P., (2010). the Design of Design: Essays

from a Computer Scientist, Addison-Wesley, Boston,

Ma, USA.

Buschmann, Frank, et al.(1996). Pattern-Oriented Software

Architecture – a System of Patterns, John Wiley, New

York, Ny, Usa.

Conselice, Christopher J. Et Al., (2016). “The Evolution of

Galaxy Number Density at Z<8 and Its Implications”,

Astrophysical Journal, 830:83, 17pp, Doi: 10.3847/

0004-637x/830/2/83.

Exman, Iaakov and Sakhnini, Rawi, (2018). “Linear

Software Models: Bipartite Isomorphism between

Laplacian Eigenvectors and Modularity Matrix

Eigenvectors”, Int. J. Software Engineering and

Knowledge Engineering, Vol. 28, Pp. 897-935. Doi:

10.1142/S0218194018400107.

Exman, Iaakov and Wallach, Harel, (2020). “Linear

Software Models: an Occam’s Razor Set of Algebraic

Connectors Integrates Modules into a Whole Software

System”, Int. J. Software Engineering and Knowledge

Engineering, Vol. 30, Pp. 1375-1413. Doi: 10.1142/

S0218194020400185.

Exman, Iaakov and Shmilovich, Alon Tsalik, (2021).

“Quantum Software Models: the Density Matrix for

Classical and Quantum Software Systems Design”,

Ieee/Acm 2

(Q-E) Int. Workshop on Quantum

Software Engineering, Pp. 1-6. Doi: 10.1109/Q-Se52

541.2021.00008

Gamma, Erich, Helm, Richard, Johnson, Ralph, and

Vlissides, John, (1995). Design Patterns – Elements of

Reusable Object-Oriented Software, Addison-Wesley,

Boston, Ma, USA.

Harel, David, (1992). “Biting the Silver Bullet: toward a

Brighter Future for System Development”, Ieee

Computer, Vol. 25, No. 1, Pp. 8-20.

Horsten, Leon, (2005). “Canonical Naming Systems”,

Minds and Machines, S. 229-257. Doi: Https://

Dx.Doi.Org/10.1007/S11023-004-6590-1

Lauer, Tod R. Et Al., (2020). “New Horizons Observations

of the Cosmic Optical Background”, Arxiv:2011.03052

[Astro-Ph.Ga]

Lenat, Douglas Et Al., (1990). “Cyc: towards Programs

with Common Sense”, Commun. Acm, 33 (8), Pp. 30-

49. Doi: 10.1145/79173.79176.

Licquia, Timothy C., Newman, Jeffrey a. and Brinchmann,

Jarle, (2015). “Unveiling the Milky Way: a New

Technique for Determining the Optical Color and

Luminosity of Our Galaxy”, Arxiv:1508.04446 [Astro-

Ph.Ga], Apj.

M1-Ultra, (2022). Apple Unveils M1 Ultra, https://www.

Apple.Com/Newsroom/2022/03/Apple-Unveils-M1-U

ltra-the-Worlds-Most-Powerful-Chip-for-a-Personal-

Computer/

Michel, Jean-Baptiste, Et Al., (2011). “Quantitative

Analysis of Culture using Millions of Digitized Books”,

Science, 331(6014), Pp 176-182. Doi: 10.1126/S

cience.1199644.

Poincare, Henri, (1914). Science and Method, Francis

Maitland (translator), Dover Publications, New York,

NY. USA.

Rising, Linda, (2001). Design Patterns in Communications

Software, Cambridge University Press, Cambridge, UK.

Schmidt, Douglas, et al., (2000). Pattern-Oriented Software

Architecture, Patterns for Concurrent and Networked

Objects, John Wiley, New York, NY, USA.

Schwartz, Stephen P., (1977). Naming, Necessity and

Natural Kinds, Cornell University Press, Ithaca, NY,

USA.

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

280