
Enhancing the Geometry of Curvilinear Sections of the Track Plan
for High-speed Traffic
Sergey Shkurnikov
1a
, Sergey Kosenko
2b
and Olga Bulakaeva
1c
1
Emperor Alexander I St. Petersburg State Transport University, St. Petersburg, Russian Federation
2
Siberian Transport University, Novosibirsk, Russian Federation
Keywords: Alignment plan, high-speed track, transition curves, curved section.
Abstract: The paper outlines the key trends in the current science of high-speed railways layout and profile design. The
employment of sophisticated laser scanning systems and satellite navigation systems simplifies the task of
constructing and maintaining complex spatial curves - areas of overlapping vertical curves in the profile and
transitional curves in the plan, sinusoidal or polynomial curves. As part of this research, a mathematical
model has been developed to describe different transition curves with non-linear curvature and elevation
characteristics of the outer rail depending on the number of zero derivatives required at the ends of the
transition curves. The shape influence (character of curvature function change within the transition curve) of
curvilinear sections of high-speed railway track plan on traffic dynamics is investigated. It has been found
that the best dynamic performance is in the curved section of the alignment equipped with transition curves
whose curvature function is represented by a 5th degree polynomial. There may also be no circular curve
within the plot in question. The paper examines the construction and mutual arrangement of differently shaped
curved sections and identifies their advantages and disadvantages.
1 INTRODUCTION
The requirements of the present development and
implementation phase of high-speed rail traffic in the
Russian Federation are shaping new approaches to the
design of the track plan and profile. As a result of
developments in the railway industry some provisions
previously considered fundamental and indisputable
are subject to critical rethinking.
The permissibility of overlapping transition and
vertical curves in the same alignment is limited by the
requirements of the existing regulatory framework
which has not lost its relevance for decades. When it
was formed in the 1960s this prohibition was justified
by the difficulty of maintaining a complex spatial
curve. However, the application of modern laser
scanning systems, GPS and GLONASS makes this
task easier. Compliance with the requirement for non-
conformity of vertical curves in the plan and
transition curves in the profile leads to an increase (up
to 33.8 % (Akkerman, 2017) in the construction cost
a
https://orcid.org/0000-0002-4273-389X
b
https://orcid.org/0000-0003-2987-1435
c
https://orcid.org/0000-0003-0982-5183
of high-speed railways (HSR). A maximum speed of
400 km/h can be realised by using large radius
vertical curves (30-40 km). The vertical curve length
is proportional to the radius, therefore longer
longitudinal profile elements are required to
accommodate vertical curves outside the transition
line which causes difficulties in routing and increases
the cost of highway construction (EN 13803-1:2010).
In order to improve the smooth running of trains
studies are being carried out on the possibility of
constructing a curve by interfacing two clothoids both
in plan and in track profile. The need for a straight
insertion between two adjacent curves in the plan,
assuming a "clothoidal" coupling, is also not obvious,
according to (Akkerman, 2017).
The regulatory value of unaccelerated speed
ensures passenger comfort when running a high-
speed train and indirectly determines the level of
permissible lateral impact of the rolling stock on the
track. In Russia the unaccelerated speed of 400 km/h
is 0,4 m/s
2
. This value is generally commensurate
200
Shkurnikov, S., Kosenko, S. and Bulakaeva, O.
Enhancing the Geometry of Curvilinear Sections of the Track Plan for High-speed Traffic.
DOI: 10.5220/0011581700003527
In Proceedings of the 1st International Scientific and Practical Conference on Transport: Logistics, Construction, Maintenance, Management (TLC2M 2022), pages 200-206
ISBN: 978-989-758-606-4
Copyright
c
2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

with the requirements of European standards
(Lindahl, 2001; Sirong, 2018). Nevertheless, Russian
research on the basis of train tests has established an
unaccelerated speed limit of 1,0 m/s
2
for high-speed
and high-speed traffic due to the improved dynamic
qualities of high-speed rolling stock. An increase in
the regulatory value of unaccelerated acceleration up
to 0.75 m/s
2
has also been noted on PRC high-speed
roads (Sirong, 2018). Increasing the allowable rates
of unaccelerated speed leads to a reduction in the
required curve radius in the plan. On the one hand,
this ensures a better alignment with the terrain,
reduces the construction and maintenance costs of
very gentle curves and on the other hand it affects the
comfort of the journey and the quality of the service
provided.
A separate area of improvement in the geometry
of the HSR route is the definition of a rational shape
of the transition curves due to the nature of the spatial
variation in curvature within its length. In addition to
the transition curves with linearly varying curvature
(clothoids) traditional for the Russian Federation
international experience distinguishes sinusoidal
(Sine (EN 13803-1:2010), cosine (Cosine (EN
13803-1:2010) and polynomial (Wiener Bogen,
Bloss) transition curves (Hasslinger, 2005; Wojtczak,
2018; Velichko, 2020). The main disadvantage of
clothoidal transition curves is that there is significant
rolling stock oscillation when traversing curved
sections of the alignment at the junctions of straight
lines with transition curves and transition curves with
circular curves (Xiaoyan, 2017; Morozova, 2020).
The cause of oscillation, in terms of the laws of
mechanics, is the piecewise linear description of the
curvature function within the length of the section in
question. Negative dynamic impacts are considered to
be compensated for by rational assignment of
transition and circular curve lengths. However, the
increased demands on traffic dynamics on the HSR
lead to the need to select a rational transition curve
shape and to determine the conditions for their
applicability.
2 MAIN TEXT
2.1 Materials and Methods
The design of transition curves on railways has been
a major focus of domestic and foreign specialists
since the beginning of the twentieth century.
Proposals G. Schramm (1931) consisted in using
some composite curves as transition curves one of
which includes two centrally symmetric segments of
a 3rd-degree parabola (Helmert curve (EN 13803-
1:2010). In the case of curves of small radii, B.N.
Vedenisov suggested using only transition curves in
the form of transformed clothoids in the absence of
circular curves. Professor G.M. Shahunyants based
on the provisions of classical mechanics analysed the
change in progressive and rotational accelerations
arising from the movement of rolling stock in a curve.
Based on this analysis, G. M. Shahunyants developed
a transition curve whose 2nd derivative curvature
varies according to a sinusoidal law. A higher
requirement for smoothness of the curvature function
is suggested by V.P. Minorski. The curvature
function of the transition curve must comply with
four boundary conditions ensuring that the 1st, 2nd,
3rd and 4th derivatives of the curvature at the start
and end of the transition curve are zero.
As mathematical basis for the transition curves
considered in the present study we propose a
polynomial В
0
, defined on the interval [0; L
ТС
],
having at least one zero derivative on the ends of the
interval. It is assumed to grow monotonically and to
take В
min
= 0 и В
max
= 1 at its beginning and end
respectively calculated by the formula:
0
,
TC
a
l
ВВ
L
=⋅
(1)
where В is a degree polynomial 1a − determined
from the condition:
1
0
1
1()
1(1) .
!
n
n
b
n
ТС
k
n
TC
l
ab
L
l
B
Ln
−
=
=
−+
∏
=+ −
(2)
In equations (1) and (2) a is the multiplicity of the
node points which determines the degree of the
polynomial sought and is numerically equal to the
value k+1, k is the number of derivatives at the ends
of the segment set as zero; l is the current value of the
length of the transition curve and L
TC
is the total
length of the transition curve (if k=0, then the
transition curve is represented as a clothoid).
The mathematical description of the function В
0
is
based on the theory of boundary conditions by V.P.
Minorsky assuming that the zero derivatives at the
ends of the segment can be more than 4. The
formation of the polynomial В
0
is realised by means
of an hermitian interpolation method.
The correlation between the function В
0
and the
curvature function k is provided by the condition:
Enhancing the Geometry of Curvilinear Sections of the Track Plan for High-speed Traffic
201
0
В
k
R
=
(3)
The curvature and elevation of the outer rail must
coincide (proportionality):
0
В
h
H
=
.
(4)
In formulae (3) and (4) R is the radius of the
circular curve, H is the elevation of the outer rail in
the circular curve, k is the current curvature within
the transition curve, h is the current elevation of the
outer rail within the transition curve.
Transition curve lengths whose mathematical
description is based on the application of the В
0
function must comply with the conditions that the rate
of wheel lift [f] and the rate of increase of
unaccelerated acceleration [Ψ] do not exceed their
maximum values laid down in the regulations. It
should be noted that as the polynomial degree В
0
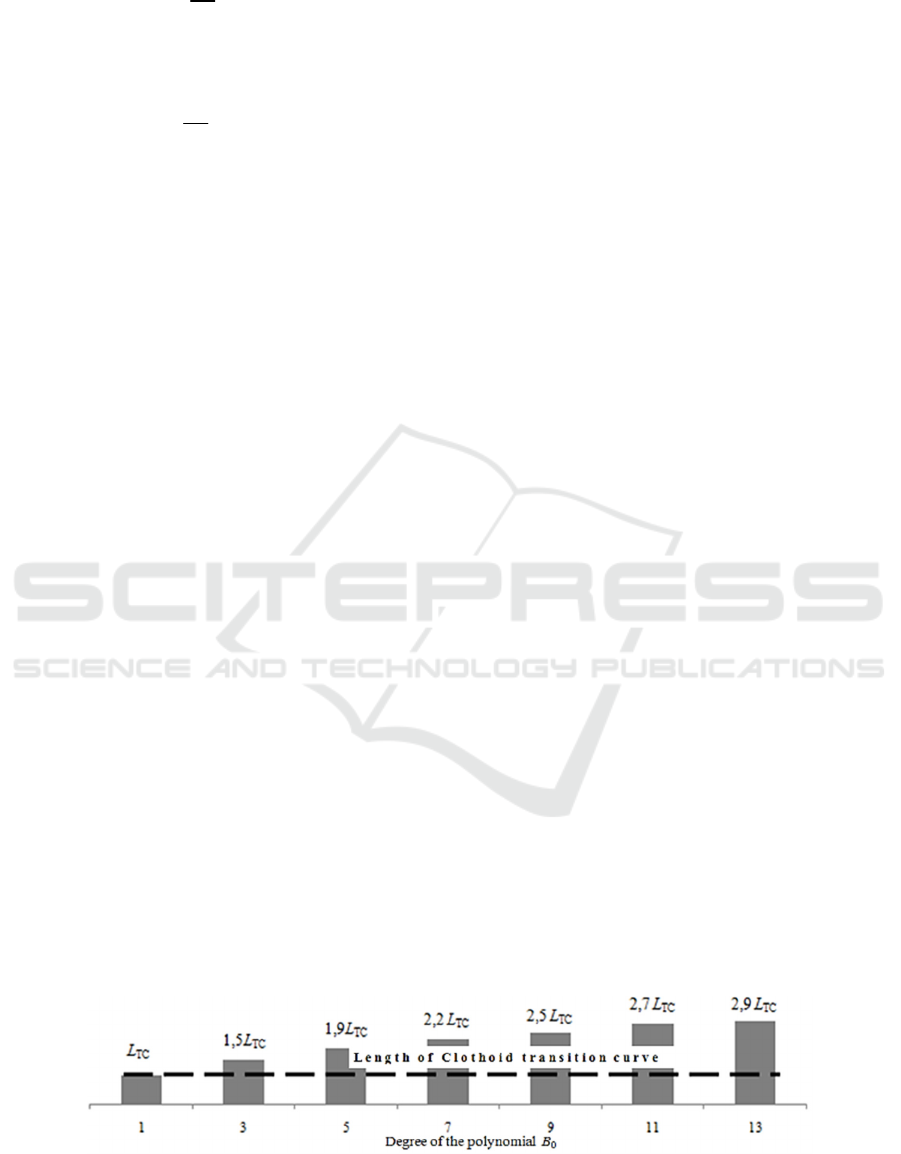
increases a lengthening of the transition curve is
required due to the magnitude of the curvature growth
rate (1st derivative of curvature) in the middle of the
transition curve. The dependence of the required
transition curve length L
ТС
on the polynomial degree
В
0
is shown in Figure 1.
In terms of the motion kinematics of a material
point on a curvilinear element the condition that the
first derivative of the curvature is zero (the third
derivative of the coordinate) at the start and end of the
transition curve is sufficient. This condition ensures
the continuity of the 'jerk' (the value ofψ on railways)
responsible for the reaction of passengers to changes
in acceleration and the safety of fragile goods. Large-
order derivatives are used quite rarely and do not even
have an approved name.
However, the movement of a railway carriage
within a curved section takes place simultaneously in
two planes: the horizontal transverse. The
translational motion and the vertical transverse - the
inclination of the carriage resulting from the ascent to
and descent from the elevation. The coordinates of the
vertical plane are proportional to the curvature. This
requirement allows the physical meaning to be
interpreted up to the third curvature derivative (the
fifth coordinate derivative):
− the first derivative of the curvature along the
length taking a zero value at the start and end
of the transition curve ensures continuity of the
additional force transient factors i, f и ψ, as well
as the angular velocity of the crew.
− the second deviation of the transition curve
turning to zero at the conjunctions with the
straight track and the circular curve ensuring
continuity of the angular acceleration.
− the third derivative of the curvature continuity
at the start and end of the transition curve
ensures that the angular acceleration rate
function or "jerk" in the vertical plane is
smooth.
2.2 Results and Discussion
2.2.1 Impact Studies of the Curved Track
Plan Shape on the Traffic Dynamics of
Highspeed Rolling Stock
The rolling stock dynamics during movement in
transition curves was investigated using a simulation
model of a high-speed vehicle (Wang, 2014) adapted
for the tasks of selecting design plan and route profile
parameters of high-speed railways using the
"Universal Mechanism" program.
A rolling stock simulation at 400 km/h was carried
out within a curved track element consisting of a
transition curve and a circular curve (R =
9400 m). The degrees of the polynomial В
0
, used to
describe the transition curves were varied from 1 to 5
within the framework of the numerical experiment
conducted. The experimental findings are shown in
Figure 2 in the form of oscillograms of unrecovered
transverse accelerations determined at the level of the
wheelset axle.
An examination of the results shows that the
maximum value of the unsuppressed transverse
acceleration (Zolotas, 2007) occurs at the interface
between the circular curve and the transition curve
Figure 1: Dependence of the required transition curve length on the degree of polynomial function В
0.
TLC2M 2022 - INTERNATIONAL SCIENTIFIC AND PRACTICAL CONFERENCE TLC2M TRANSPORT: LOGISTICS,
CONSTRUCTION, MAINTENANCE, MANAGEMENT
202
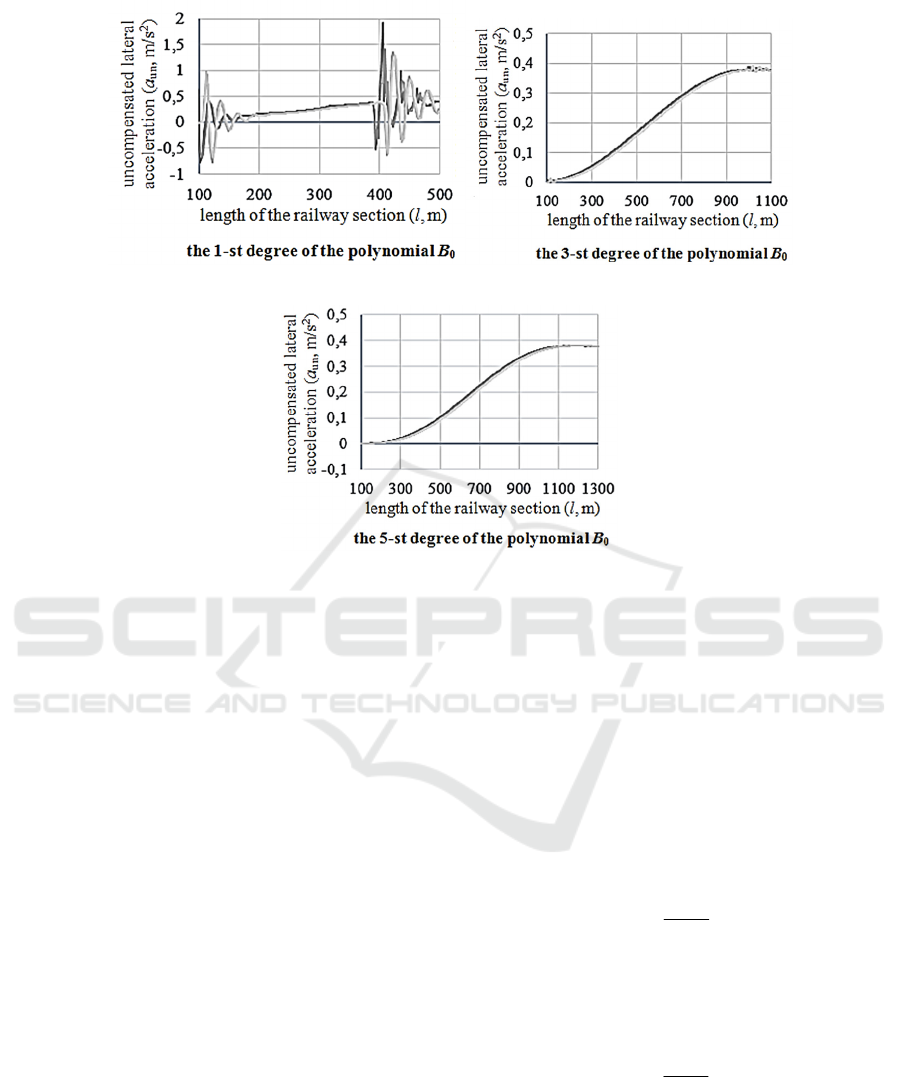
a) b)
c)
Figure 2: Oscillograms of lateral acceleration during high-speed rolling stock movement within differently shaped transition
curves.
whose curvature function is represented by a
polynomial of degree 1. The maximum actual value
of the unrelieved lateral acceleration
act.
unv.max
a is 2.0
m/s
2
and is several times greater than the calculated
value
сalc.
unv.max
a
(0.4 m/s
2
at a circular curve radius of
9400 m). Transition curves whose curvature function
is described by 3rd- and 5th-degree polynomials are
overcome without additional rolling stock
oscillations (
act.
unv.max
a
≈
сalc.
unv.max
a
.
).
The curved alignment shape is determined not
only by the degree of the transition curve polynomial
used to describe the curvature function but also by the
presence or absence of a circular curve. Figure 3
shows the simulation results for movement within
differently shaped curved sections.
According to the results obtained (Fig. 3 and Fig.
4) when organising high-speed rail traffic at 400 km/h
the best dynamic performance is in the curvilinear
section of the route plan equipped with transition
curves whose curvature function is represented by a
polynomial of degree 5. There may also be no circular
curve within the plot in question.
2.2.2 Features of the Arrangement and
Relative Positioning of Differently
Shaped Curvilinear Sections
A pie chart is developed to compare the device
requirements for non-linear curvature sections
arranged in series and traditional curvature:
− the minimum rotation angle
α
min
required to
construct a curved section of radius
R (sequence
of steps 1-2-3 in Figure 4);
00
min
R
R
α
α
=
(5)
−
Determination of the minimum radius
R
min
required to construct a curved section at a given
α
(sequence of steps 4-5-6 in Figure 4);
00
min
R
R
α
α
=
(6)
On the presented diagram Table 1 is filled in to
clearly evaluate the advantages and disadvantages of
the different shapes of the curved sections of the
alignment plan.
Enhancing the Geometry of Curvilinear Sections of the Track Plan for High-speed Traffic
203

Figure 3: Magnitudes of unaccelerated acceleration in the crew bed occurring when driving within curved sections of different
shapes.
Table 1: Curved sections of different shapes.
Comparative characteristics
Swivel an
g
le 10°
В
0
p
ol
y
nomial of de
g
ree 1
В
0
p
ol
y
nomial of de
g
ree 5
Set / minimum radius of curved section, m 5000 5400
Length of transition curve, m 500 940
Total plot length, m 1373 1876
Length of constant curvature section, m 373
–
Bisector of the curved section, m 21 24
An obvious disadvantage of curvilinear sections
that include transition curves with a curvature
function described by a 5th degree polynomial is that
their length increases (1.36 times in the case in
question). However, for small alignment angles
(
α<α
min
) the required radius of the curved section
consisting of two transitional curves of non-linear
curvature increases thereby ensuring a reduction in
operating costs in the curve.
3 CONCLUSIONS
The result of this study allows us to change the usual
perceptions of the curved section of the high-speed
rail track plan. The best shape in terms of driving
dynamics is the curvilinear section within which the
additional oscillations of the crew tend to zero.
Equipping a curved section with transition curves
whose curvature and elevation divergence functions
are represented by5th degree polynomials meets these
requirements. The circular curve may not be present
at all in the section or may be smaller than the
standard value.
Despite better dynamic performance the length of
these transition curves is almost twice as long. It must
be taken into account that the permissible standard
values [
f] and [Ψ] have been determined for
clothoidal transition curves. It should be taking into
account the significant oscillations of the rolling stock
when passing through curved sections of the
alignment at the junctions of straight, transition and
circular curves. The implementation of transient
curves with non-linear curvature leads to the
complete damping of this kind of oscillation which
theoretically leads to an increase in the tolerance rates
[
f] и [Ψ]. Increasing these values contributes to
reducing the required length of the transition curves.
TLC2M 2022 - INTERNATIONAL SCIENTIFIC AND PRACTICAL CONFERENCE TLC2M TRANSPORT: LOGISTICS,
CONSTRUCTION, MAINTENANCE, MANAGEMENT
204

Figure 4: Pie chart for determining curvilinear section design features.
At the present stage of the study in the curvature
design of the high-speed railway alignment plan it is
recommended to replace the traditional curvature
sections with polynomial (
В
0
polynomial of degree 5)
transition curves, conjugate without circular curve in
cases of small alignment angles (
α<α
min
). For an
unbiased assessment of other design cases (
α
min
>α )
the installation of an experimental curvilinear section
and a train test to assess the possibility of increasing
the tolerances [
f] and [Ψ] is necessary.
REFERENCES
Akkerman, G. L., Akkerman, S. G., 2017. High-speed
railway highlights. Herald of the Ural State University
of Railway Transport. 2 (34). pp. 46-56.
EN 13803-1:2010: Railway applications – Track – Track
alignment design parameters – Track gauges 1435 mm
and wider - Part 1: Plain line [Required by Directive
2008/57/EC].
Lindahl, M., 2001. Track geometry for high-speed
railways: A literature survey and simulation of dynamic
vehicle response. Stockholm, TRITA-FKT Report,
Royal Institute of Technology. p. 160.
Sirong, Y., 2018. Dynamic analysis of high - speed railway
alignment: theory and practice. Academic Press. 324 p.
Hasslinger, H., 2005. Measurement proof for the
superiority of a new track alignment design element, the
so- called Viennese Curve” Berlin. ZEVrail. 129. pp.
61-71.
Wojtczak, R., 2018. General equation of cant ramp in form
of polynomial of odd degree.
https://www.researchgate.net/.
Wang, K., Zhai, W, 2014. Study on performance matching
of wheel-rail dynamic interaction on curved track of
speed-raised and high-speed railways. China Railway
Science, 35(1). pp. 142-144.
Velichko, G., 2020. Quality analysis and evaluation
technique of railway track + vehicle system
performance at railway transition sections with various
shape curves. Transport Means 2020 Proceedings of
the 24th International Scientific Conference Part II: pp.
573-578.
Enhancing the Geometry of Curvilinear Sections of the Track Plan for High-speed Traffic
205

Xiaoyan, Lei, 2017. High speed railway track dynamics:
models, algorithms and applications. p. 414.
Long, X. Y., 2008. Study on dynamic effect of alignment
parameter on train running quality and its optimization
for high-speed railway.
Morozova, O. S., Shkurnikov, S. V., 2020. The
substantiation of design parameters of circular curves
on high-speed railways. Modern Technologies. System
Analysis. Modeling. 3 (67). pp. 152-159.
Zolotas, A. C., Goodall, R. M. Halikias, G. D., 2007. Recent
results in tilt control design and assessment of high
speed railway vehicles. Proc. ImechE Part F: J. Rail
and Rapid Transit. 221. pp. 291-312.
TLC2M 2022 - INTERNATIONAL SCIENTIFIC AND PRACTICAL CONFERENCE TLC2M TRANSPORT: LOGISTICS,
CONSTRUCTION, MAINTENANCE, MANAGEMENT
206
