Sensitivity and Permissible Deviation in Electric Track Circuits

Yuri I. Zenkovich and Anton А. Antonov

Russian University of Transport RUT (MIIT), Moscow, Russia

Keywords: Track circuit, permissible deviation of parameters, input resistance stabilization, input impedance.

Abstract: New expressions have been obtained for assessing the sensitivity and permissible deviations of the electric

track circuit elements parameters, allowing to evaluate their influence on the implementation of the shunt

and control modes of operation of the track circuits.

1 INTRODUCTION

Track circuits in railway automation devices are

used as the main sensor for monitoring the state of

the rail line. There are three main states of the rail

line. The rail line (RL) is free of rolling stock, the

RL is occupied by rolling stock, the RL has a break

in one of the rails. These states have the

corresponding names: normal, shunt and control

modes of operation of the track circuit. The

determining modes of operation in terms of meeting

the requirements for the safety of train traffic are

shunt and control modes. Failure to comply with

these modes leads to catastrophic failures in the

transportation of passengers and goods by rail

(Lisenkov, 1999; Lee, 2013; Moine, 2019; Spunei,

2018; Efanov, 2019).

It is known that the task of synthesizing track

circuits is to determine the maximum length of the

rail line and the input resistance at the ends of the

rail line, in which the shunt and control modes are

performed. Energy ratios, which are associated with

the optimization of the transmission of electrical

energy from one (transmitter) end of the rail line to

the other (relay) end, are secondary.

The choice of the input resistance value at the

ends of the electric rail line is due to the

simultaneous fulfillment of the criteria of the shunt

mode

𝑠

=𝑓

(

𝑍

)

and the control К

𝑐

=𝑓

(

𝑍

)

for the maximum allowable length of the rail line.

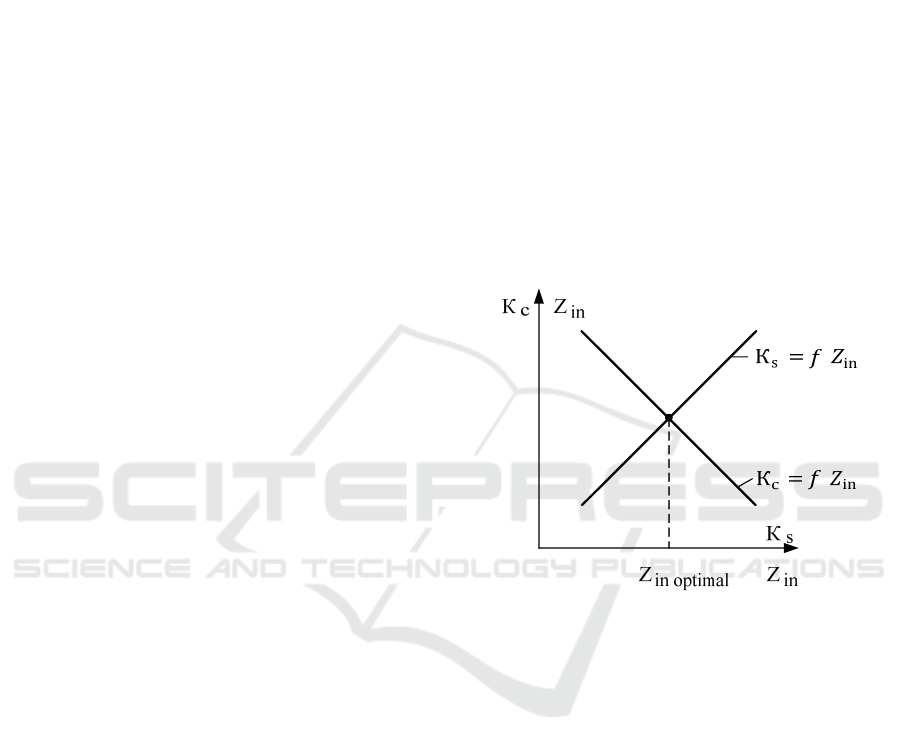
Figure 1 shows the dependences of the criteria for

the shunt and control modes of operation of the track

circuit on the input resistances at the ends. (Arkatov,

1990)

Figure 1: The dependences of the criteria for the shunt and

control modes of operation of the track circuit.

As can be seen from Figure 1, the dependences

under consideration represent mutually inverse

functions, so the intersection point determines the

optimal value of

𝑍

at which the shunt and control

modes are performed. It also follows from the graph

that the deviation from the optimal value leads to an

improvement in one of the modes and a deterioration

in the other.

To exclude catastrophic failures due to violation

of the operating modes of track circuits, it is

necessary to stabilize the input resistances at the

ends of the rail line. However, in the operation of

track circuits, situations occur that the input

resistances at the ends of the track line are subject to

change. At the same time, it is important that the

changes are within the specified tolerances, so that

with the accepted tolerances, taking into account the

accepted safety factors, the specified modes are

ensured.

Zenkovich, Y. and Antonov, A.

Sensitivity and Permissible Deviation in Electric Track Circuits.

DOI: 10.5220/0011587100003527

In Proceedings of the 1st International Scientiﬁc and Practical Conference on Transport: Logistics, Construction, Maintenance, Management (TLC2M 2022), pages 355-358

ISBN: 978-989-758-606-4

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

355

At the second stage of the synthesis of track

circuits, the configuration of the input resistances of

the track circuit is selected based on the given

impedance of the input resistance. When choosing

elements to create a given impedance, energy

relationships are taken into account, but issues

related to the analysis of tolerances that determine

the effect of deviation of any parameter of the input

resistance impedance from its nominal value are not

taken into account.

2 MATERIALS AND METHODS

At the second stage of the synthesis of track circuits,

the problem of tolerances is associated with the

choice of such equivalent circuits that have minimal

tolerances. In the case of structural synthesis, the

achievement of minimum tolerances can be

considered as an independent task. This problem can

be partially solved by using the methods of analysis

and synthesis, however, significantly new results can

be obtained if the knowledge of tolerances is used in

the optimization process in the structural synthesis

of input resistances at the ends of the rail line.

Changing the input impedance values of the

track circuit elements is undesirable from the point

of view of tolerance theory. However, this

disadvantage can be used as a positive factor in

optimization. The connection between the parameter

space of input resistance impedance elements and

tolerance optimization is carried out using the

sensitivity of the circuit function (Lanne, 1969),

which can be defined as a partial derivative:

𝑆



𝑑 𝑦

𝑑 𝑥



=

𝜕 𝑍



𝜕 𝑍





(1)

Sensitivity plays an important role in

determining the parameters of the circuit elements of

the input resistance

𝑍

depending on the

configuration of the electrical circuit and the values

of its elements

𝑍

𝑖

. Thus, the sensitivity of the

characteristic of the input impedance of the end of

the track circuit is a function of the parameter

𝑍

𝑖

The deviation of the characteristic of the input

resistance

𝑍

𝑖

from the optimal values is defined as

∆𝑍



=𝑆



∆𝑍







(2)

The relative sensitivity, in turn, can be defined

as:

𝑆





𝜕ln𝑍



𝜕𝑙𝑛𝑍



𝑍



𝑍



𝑆



=𝑆





(

𝑍



,𝑍



)

(3)

The relative deviation of the input resistance 𝑍

𝑖

is equal to

∆Z



𝑍



=𝑆









∆Z



𝑍



(4)

When calculating the electrical circuit of the

input resistance, it is assumed to use, first of all,

relative units (Ablin, 1970; Holt, 1969).

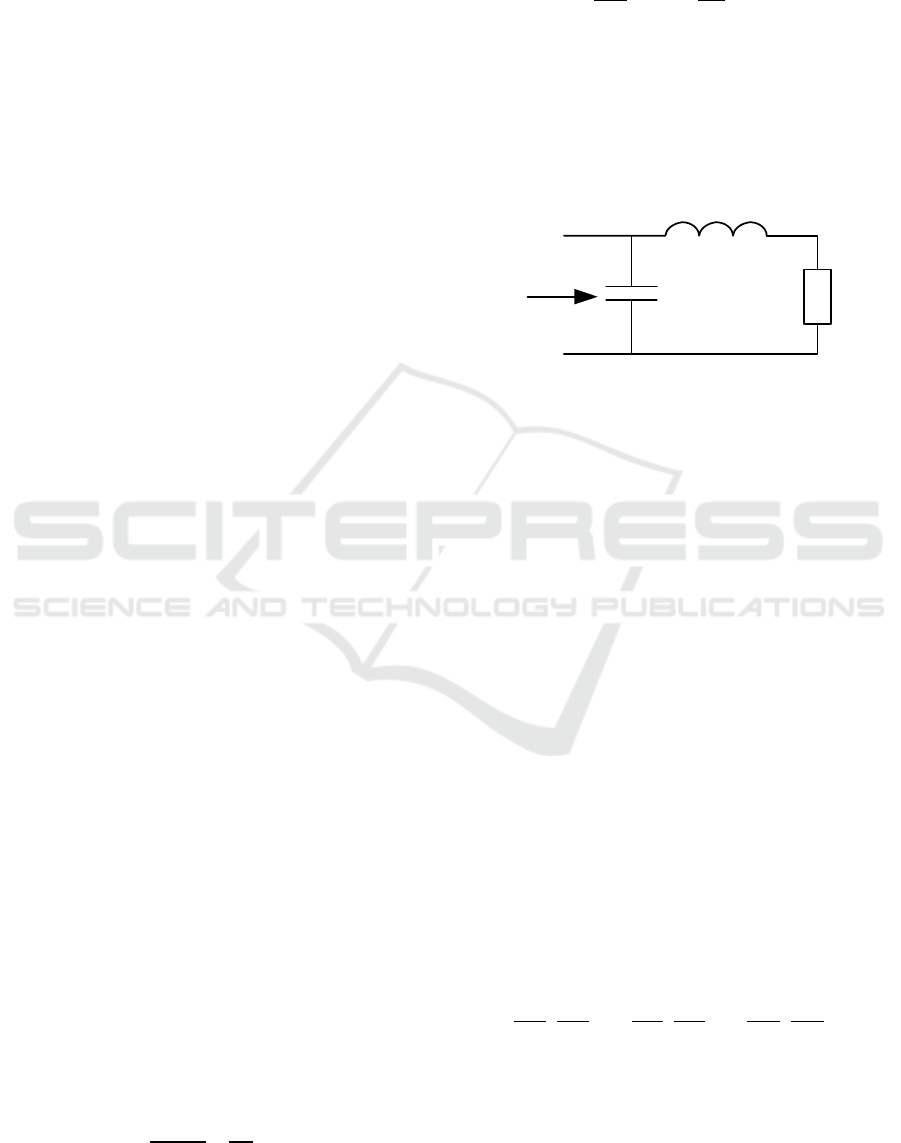
Consider the issue of using relative units on the

example of the circuit shown in Figure 2.

Figure 2: Circuit input impedance.

For the presented circuit in Figure 2, arbitrary

circuits can be obtained by choosing the normalized

values R, L, C, ω in relative units. With an increase

in λ times the units of measurement, and the

simultaneous invariance of the unit of measurement

of the frequency ω, the impedance of the input

resistance

𝑍

𝑖

will increase by λ times. For the

convenience of mathematical analysis, we separate

the values of resistance, inductance and capacitance

in the impedance

𝑍

𝑖

We introduce the reciprocal values of the

capacitance and denote them by D. Then we obtain

the expression for the impedance

𝑍



=𝑍(𝑅



…𝑅



,𝐿



…𝐿



,𝐷



….D



,𝜔), where 𝑁



𝑁



+𝑁



=𝑁.

For the impedance, the following relationship

holds.

𝑍



=𝑍

(

𝜆𝑅



…𝜆𝑅



,𝜆𝐿



…𝜆𝐿



,𝜆𝐷



….𝜆𝐷



,𝜔

)

=𝜆𝑍

(

𝑅



…𝑅



,𝐿



…𝐿



,𝐷



….D



,𝜔

)

(5)

𝑍



=𝑍

(

𝜆𝑅



…𝜆𝑅



,𝜆𝐿



…𝜆𝐿



,𝜆𝐷



….𝜆𝐷



,𝜔

)

=𝜆𝑍

(

𝑅



…𝑅



,𝐿



…𝐿



,𝐷



….D



,𝜔

)

Z – linear homogeneous function of variables R, L, D.

Differentiating Eq. (5) with respect to λ, we obtain:



𝜕𝑍



𝜕𝜆𝑅



∙

𝜕𝜆𝑅



𝜕𝜆

+

𝜕𝑍



𝜕𝜆𝐿



∙

𝜕𝜆𝐿



𝜕𝜆







𝜕𝑍



𝜕𝜆𝐷



∙

𝜕𝜆𝐷



𝜕𝜆𝐷











=𝑍



(6)

From expression (6), expression (7) follows

TLC2M 2022 - INTERNATIONAL SCIENTIFIC AND PRACTICAL CONFERENCE TLC2M TRANSPORT: LOGISTICS,

CONSTRUCTION, MAINTENANCE, MANAGEMENT

356



𝑅



𝑍



∙

𝜕𝑍



𝜕𝜆𝑅



+

𝐿



𝑍



∙

𝜕𝑍



𝜕𝜆𝐿









𝐷



𝑍



∙

𝜕𝑍



𝜕𝜆𝐷











(7)

Using expressions (1), (2) and (3) together with

expression (7), we obtain (8).

𝑆





(

𝑍



,𝑅



)

+𝑆





(

𝑍



,𝐿



)





𝑆





(

𝑍



,𝐷



)









(8)

In another way, using the common sign of the

sum, we get:

𝑆





(

𝑍



,𝑍



)





)

Using expression (9), the sum of the relative

sensitivities of the impedance

𝑍

𝑖

, considering it with

respect to R, L, and also D=1/C, is equal to 1. Using

the sensitivity invariant, a number of useful results

can be obtained when solving the problem of

optimizing the input resistances at the ends of the

rail line, in particular when calculating the input

impedance having a minimum sensitivity

(Fjallbzant, T. 1969; Tomovich, 1972; Nekrasov,

2001; Nekrasov, 2002).

When analyzing tolerances for deviations of

input resistances at the ends of a rail line, various

assumptions can be made regarding the law of

addition of partial deviations Δ𝑍

 

=𝑆



Δ𝑍



. But at

the same time, the issue of calculating the worst case

deviation of the input resistance can be considered

∆𝑍

 

𝜀=

𝑆



𝛥𝑍



=

𝑆



𝑑











(10)

ε defines the maximum allowable deviation, and

𝑑



is the maximum change in the value of the circuit

element. This method can be used in the synthesis of

track circuits in the case of deterministic deviations

of the input resistance elements, when the number of

elements included in the electrical circuit is not

large.

From expression (10) 𝑑



is determined according

to the following algorithm. We accept that the

maximum permissible deviation ε and sensitivity 𝑆



are known. We also accept that for all elements of

the circuit the absolute values of partial deviations

𝑆



𝑑



will be the same. Thus, there is a chain with a

uniform distribution of partial deviations. Then it is

possible to determine partial deviations, knowing the

ratio of the maximum permissible deviation ε to the

number of circuit elements N:

𝜀

𝑁



𝑆



𝑑



(11)

From here we can calculate the absolute

tolerance of the electrical circuit element

𝑑



𝜀

𝑁

𝑆





(12)

3 CONCLUSIONS

Summing up the above reasoning, we can conclude

that if the corresponding sensitivity is small, then the

circuit element will have a large tolerance and vice

versa. Each element of the circuit makes the same

contribution to the deviation of the characteristic of

the circuit. When the number of circuit elements is

large (more than 5 in practice), relation (12) gives

very small tolerances for the electrical circuit

elements. (Nekrasov, 2016; Lisenkov, 2014).

In the case of statistical calculation of deviation

tolerances and input resistances, partial deviations

can be considered as random variables, and a certain

probability of failures (rejection) is allowed. The

input resistance circuit is rejected if

∆𝑍

 

=𝑆



∆𝑍







𝜀

(13)

To determine the probability 𝑃(

∆Z



𝜀) of

rejection, we introduce a random variable μ and

determine the basic properties and addition laws of

this variable. Assume the existence of a probability

density function μ and denote this function by P(x).

Then the probability of an event μ <x is defined as

𝑃

(

𝜇𝑥

)

=𝑃

(

𝑥

)

𝑑𝑥





(14)

and the mathematical expectation will look like

(

𝜇

)

=𝑥𝑃

(

𝑥

)

𝑑𝑥





(15)

In turn, the variance will be defined as

𝐷



(

𝜇

)

=𝑀



𝜇𝑀



𝜇





=

(

𝜇𝑀𝜇

)



𝑃

(

𝑥

)

𝑑𝑥





(16)

When calculating deviation tolerances

statistically, it is necessary to know the actual

distribution of the parameters of the elements

included in the electrical circuit of the input

impedance of the end of the rail line. (Nekrasov,

2001)

Sensitivity and Permissible Deviation in Electric Track Circuits

357

However, with the real distribution of element

parameters, one can always associate the Gaussian

distribution with the same mathematical expectation

and variance. Then statistical calculations can be

easily carried out for the obtained tolerances of

deviations of input resistances at the ends of the rail

line.

REFERENCES

Lisenkov, V. M., 1999. Statistical theory of train traffic

safety. p. 325.

Lee, M.-C., Park, J.-Y., 2013. A study on the length of

electrical separation joint in AF track circuit.

Transactions of the Korean Institute of Electrical

Engineers. 62 (1). pp. 70-75.

Moine, E. H., Hassane, M., Marouane, E. A., 2019.

Parameter estimation and fault diagnosis for

compensation capacitators in ZPW-2000 jointless

track circuit. International Conference on Wireless

Technologies, Embedded and Intelligent Systems,

WITS 2019. 8723777.

Spunei, E., Piroi, I., Muscai, C., Răduca, E., Piroi, F.,

2018. Track circuits diagnosis for railway lines

equipped with an automatic block signalling system.

IOP Conference Series: Materials Science and

Engineering. 294(1), 012014.

Efanov, D. V., Osadchy, G. V., Khoroshev, V. V.,

Shestovitskiy, D. A., 2019. Diagnostics of Audio-

Frequency Track Circuits in Continuous Monitoring

Systems for Remote Control Devices: Some Aspects.

IEEE East-West Design and Test Symposium on

Electromagnetic Compatibility. 8872092, pp. 550-555

Arkatov, V. S., Kravtsov, Yu. A., Stepenskiy, B. M., 1990.

Track circuits. Analysis of work and maintenance. p.

295.

Lanne, A. A., 1969. Optimal synthesis of linear electrical

circuits. p. 301.

Ablin, A. I., Khotuntsev, Yu. L., 1970. Stability of a

regenerative amplifier with a spread of all

parameters. XIII. 11. pp. 1389-1391.

Holt, A. C., Lee, M. R., 1969. General Rule for the

Compensation of the Sensitivity of Networks to its`

Active Devices. Electron Letters. 5. 14. pp. 324-325.

Fjallbzant, T. 1969. Active Network Synthesis. Ericsson

Technics, Stockholm. 1. pp. 3-52.

Tomovich, R., Vukobratovich, M., 1972. General theory

of sensitivity. p. 360.

Nekrasov, S. A., 2001. Interval methods and algorithms of

global nonlinear optimization and their application to

designing electrotechnical devices. Part I.

Elektrichestvo. 8. pp. 43-49.

Nekrasov, S. A., 2002. Using the interval and bilateral

methods for optimizing the design of electro-magnets

under conditions of inexact specified initial data. Part

2. Elektrichestvo. 7, pp. 54-58.

Nekrasov, S. A., 2016. A numerical method for solving

dynamical systems with lumped parameters which

accounts for an input data error. Journal of Applied

and Indus- trial Mathematics, 10 (4), pp. 528-537.

Lisenkov, V. M., 2014. Methods for analysis and synthesis

of track circuits (statistical approach). p. 221.

TLC2M 2022 - INTERNATIONAL SCIENTIFIC AND PRACTICAL CONFERENCE TLC2M TRANSPORT: LOGISTICS,

CONSTRUCTION, MAINTENANCE, MANAGEMENT

358