
The Research of Probability of Informed Trading under Short-Sell
Constraints
Jingxia Xu
1, 2, a*
, Susheng Wang
3, b
, Jijin Geng
2, c
and Yun Xiong
4, d
1
School of Urban Planning and Design, Peking University, Nanshan District, Shenzhen, Guangdong, 518000, China
2
Shenzhen Land and Real Estate Exchange Center, Futian District, Shenzhen, Guangdong, 518000, China
3
Finance Department, South University of Science and Technology, Nanshan District, Shenzhen, Guangdong, 518000, China
4
Ping An Bank Co., Ltd, Shenzhen, Guangdong, 518000, China
Keywords: Short-Sell Constraints, Probability of Informed Trading, Trading Spread.
Abstract: The probability of informed trading is an important indicator for regulators supervising market order. Classic
models of the probability of informed trading allow traders short unlimited with private information.
However, it has short-sell constraints in China's stock market at present, which would make the measurement
deviation occurs if directly apply classic models to China's stock market. Under this condition, this research
adds two short-sell constraint parameters to the classic model, named SC-TPIN model, to measure the
probability of informed trading of stocks with bad event. By selecting eligible stocks as the sample stocks,
this research estimates the probability of informed trading and relevant parameters of those stocks before and
after the disclosure day, and analyze and summarize the time characteristics and microscopic characteristics
of these parameters. This research proves that the SC-TPIN model is consistent with the order flow
information, and the parameters and probability of informed trading estimated by the SC-TPIN model are in
line with the actual situation of sample stocks. Compared with the TPIN model, the SC-TPIN model has
strong explanatory power in explaining the same time series spreads and strong predictive power in
forecasting future spreads in China’s stock market. Therefore, the SC-TPIN model is valid.
1 INTRODUCTION
The supervision on the insider trading caused by bad
events is somewhat weakness in China’s stock market
at present. We consult insider trading events handled
by China Securities Regulatory Commission, and
find that these insider trading cases are mainly caused
by good events, rarely relate to bad events. Since
2011, there are only 4 insider trading cases caused by
bad events, meanwhile, there is no bad insider trading
case relate to underlying stocks of margin trading,
which show that the regulation of insider trading
caused by bad events should be improved. Insider
trading is part of informed trading, and the regulation
on informed trading can effectively prevent insider
trading events to occur. The probability of informed
trading model is a feasible method to infer informed
trading and observe the dynamic change of
probability of informed trading. There are short-sell
constraints in China’s stock market at present.
Effectively calculating stocks’ probability of
informed trading under China's current market
condition, screening stocks with higher probability of
informed trading, and hosting supervision on such
stocks, could provide a feasible direction for
regulating insider trading caused by bad events in
China's stock market.
The informed trading measurement model which
accepted widely is EKOP model proposed by Easley
(1996) (Easley, 1996), known as the classical EKOP
model. The EKOP model reflects the situation of
informed trading through the imbalance of orders,
that is, the order arrival rate of informed traders and
uninformed traders are different due to the differ of
their private information. Although the model is
found by observing the rules of the market maker, its
principle can also be applied to the order driven
market. For example, Yang et al. (2004) assumes that
there is a hidden market maker who makes deal with
informed and uninformed investors through
submitting limit orders, and they applied the EKOP
model directly to the Shanghai Stock Exchange
(Yang, 2004). Many scholars have improved the
model in order to correctly estimate the probability of
Xu, J., Wang, S., Geng, J. and Xiong, Y.
The Research of Probability of Informed Trading under Short-Sell Constraints.
DOI: 10.5220/0011731700003607
In Proceedings of the 1st International Conference on Public Management, Digital Economy and Internet Technology (ICPDI 2022), pages 137-144
ISBN: 978-989-758-620-0
Copyright
c
2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
137

informed trading under various trading rules. such as
Qin Lei (2005) (Lei, 2005) had research on the New
York Stock Exchange and found that the buy and sell
order arrival rate of uninformed traders are different,
so they introduced the TPIN model by setting the buy
and sell order arrival rate of uninformed traders with
different parameters based on the classic EKOP
model. The model is rational and reasonable through
deduction and demonstration, and is used by more
and more scholars. Duarte and Young (2009)
proposed a modified PIN model. They added the
market order flow shock in the classical EKOP
model, which make the correlation of buy and sell
orders implied in the model positive, in order to better
match the actual data (Duarte, 2009).
No matter the classic EKOP model, nor the TPIN
model, they both don’t involve short-selling
constraints, and default that trader can short freely.
While in China's stock market, naked short is
forbidden, and traders could short only when they
reach a certain threshold, which restrict lots of traders
to short. Therefore, if we want to calculate the
probability of informed trading accurately, we should
choose models involving short-sale constraint
variables. Yuan et al. (2011) (Yuan, 2011) divide the
short-sale constraint into four types, and divide
traders into full short selling, restricted short selling,
prohibited short selling, and selling, and set
parameters for those traders respectively. Parameters
of this model are too many, and some traders may sell
and short sell at the same time, which may lead to
repeating calculations. Wang, Guo et al (2013, 2013)
(Guo, 2013; Wang, 2013) introduced a short-sale
constraint factor
θ
into the classical EKOP model,
with
10 <<
θ
, then the model became
)2)1(/()1(
ε
θ
δ
δ
α
μ
θ
δ
δ
α
μ
++−+−=PIN
. Due to
10 <<
θ
, the PIN value calculated by this model is
less than the PIN value calculated by the EKOP
model. When good news come, informed traders
would buy stocks, and in this case there is no short
selling restrictions, but because
0≠
θ
and
1≠
θ
, the
PIN value estimated by the model would not match
with actual situation.
Considering the status quo of short-sell
constraints in China’s stock market, we build the SC-
TPIN model through adding two short-sell constraint
parameters to the TPIN model and deducing the
model equation by using the decision tree. Then we
illustrate step by step that our SC-TPIN model is
suitable for current China’s stock market by order
information flow derivation, estimation results
analysing, explanatory power and predictive power
verification to the information asymmetry proxy
indicator. We prove that our SC-TPIN model is more
effective in estimating stocks’ probability of
informed trading in China's stock market compared
with TPIN model, which provide a reference for
measuring probability of informed trading of stocks
caused by bad events in China's stock market.
The contents of this paper are as follows: the
second part is the model construction, we construct
our SC-TPIN model and deduce its order information
flow. The third part is the empirical results analysing,
we analyse the distribution of SCTPIN value and
parameters from the perspective of time and micro
characteristics. The fourth part is the model validity
verify, we analyse the sensitivity of short-selling
constraint parameters, and verify the explanatory
power and predictive power of SCTPIN value to the
trading spread. The fifth part is the conclusion.
2 MODEL CONSTRUCTION
China's securities market sets different restrictions on
financing trading and short selling, and investors
react different to good news and bad news (Xie,
2015). In order to make the model correctly reflect
the actual market situation, we only take into account
the calculation of the probability of informed trading
of stocks with bad events happened in this paper.
Based on the TPIN model proposed by Qin Lei
(2005) (Lei, 2005), we add short-sell constraint
parameters into the TPIN model, and get our
probability of informed trading model which could be
used under short-sell constraint condition, denoted as
Short-sale Constraint TPIN model (SC-TPIN model).
This model is mainly used to calculate the probability
of informed trading of stocks with bad events under
the condition of short-sell constraint. The value of the
probability of informed trading estimated by the SC-
TPIN model is recorded as SCTPIN value.
2.1 TPIN Model
There are three kinds of information state in the stock
market: good news, bad news and no news. At the
beginning of each trading day, information events are
independently distributed and occur with probability
α
, and the information is only mastered by informed
traders. The probability that the information is bad
news is
δ
, while that good news is
δ
-1
. Assuming
that the buy and sell order arrival rate of uninformed
traders in one day submit to the Poisson distribution
with parameter of
b
ε
and
s
ε
respectively. When the
information arrives, the order arrival rate of informed
ICPDI 2022 - International Conference on Public Management, Digital Economy and Internet Technology
138

traders submits to the Poisson distribution with
parameter of
μ
.
By using the high-frequency transaction data, we
can estimate parameters above from the maximum
likelihood estimation bellow:
!!
)(e
)-1(
!
)(
!
e
!!
e
-1),(
)(
)(
S
S
e
B
S
e
BS
e
B
SBL
S
s
B
b
S
s
B
bs
B
b
sb
sbsb
εμε
δα
μεε
αδ
εε
αθ
εμε
μεεεε
+
+
+
+=
+
+
)(
(1)
Then we can get the value of TPIN
)(
αμεεαμ
++=
sb
TPIN
(2)
2.2 Short-Sale Constraint TPIN Model
(SC-TPIN Model)
The TPIN model assumes that when informed traders
learn the information of one stock arrives, they can
trade according with their private information
without cost and restriction. However, if there are
short-sale constraints in the market, or even lack of
short mechanism, it would prevent informed traders
to short, and change the distribution of market
information.
At present, China's stock market has the following
short-sale constraints: only underlying stocks of
margin trading are allowed to be shorted; naked short
selling is not allowed; the cost of short selling is
higher, only investors who meet a certain threshold
are allowed to short, and the securities lending
amount of those investors is also limited by their
credit and margin line. In this case, uninformed
traders usually behave as liquidity traders or noise
traders. Short restriction and high threshold of margin
trading will prevent uninformed traders to short,
while informed traders will choose to short only when
they have strong sign that the price is going to fall.
Therefore, margin trading distinguishes informed and
uninformed traders to some extent.
According to the TPIN model, we still assume
that the information arrive rate is
α
, and the
information is only mastered by informed traders.
The probability that the information is bad news is
δ
, while that good news is
δ
-1
. The buy and sell
order arrival rate of uninformed traders on one day
submit to the Poisson distribution with parameter of
b
ε
and
s
ε
respectively. When the information arrives,
under the unlimited shorting status, the order arrival
rate of informed traders submits to the Poisson
distribution with parameter of
μ
. We assume that the
proportion of informed traders who hold the target
stock is
h
,
10 ≤≤ h
, and informed traders prefer to
sell their holding first. The proportion of informed
traders who short the target stock is
k
, and
10 ≤≤ k
.
So when the bad news of one stock arrives, informed
traders who hold the target stock will take sale or
short sell strategy, this part of informed traders is
h
,
the proportion of informed traders who don’t hold the
target stock but short it is
kh)-1(
, while the
proportion of informed traders who do not hold the
target stock and cannot short it because of short-sell
constraints is
)1)(1( kh −−
.
Other assumptions of this model are consistent
with other probability of informed trading models
without short-selling constraints. The transaction
process can be described by the decision tree of figure
1.
Figure 1: The decision tree existing short-sell constraints.
Information
event occurs
Bad news
Sell arrival rate
Buy arrival rate
Sell arrival rate
Buy arrival rate
Sell arrival rate
Buy arrival rate
Information event doesn’t
occur
Good news
Once per day
The Research of Probability of Informed Trading under Short-Sell Constraints
139

After introduce parameters of h and k, the order
arrival rate of informed traders is
)1())1((
δ
α
μ
α
μδ
−+−+ khh
And the order arrival rate of uninformed traders is
sbsbsbsb
ε
ε
ε
ε
α
ε
ε
δ
α
ε
ε
α
δ
+=+−++−++ )))((1())(1()(
Thus the probability of informed trading is
sb
sb
khh
khh
khh
khh
PIN
εεδδαμ
δδαμ
εεδαμαμδ
δαμαμδ
++++
++
=
++++
++
=
]-1))-1(([
]-1))-1(([
)-1())-1((
)-1())-1((
(3)
The maximum likelihood estimation is adopted to
estimate unknown parameters in the SC-TPIN model.
In this case, the likelihood estimation function of
parameter
T
sb
kh ),,,,,(
μεεδαθ
=
is
!!
)(e
)-1(
!
)])-1(([
!
e
!!
e
-1),(
)(
)])-1(([
S
e
B
S
khhe
B
S
e
B
SBL
S
s
B
b
S
s
khh
B
b
S
s
B
b
sb
sb
sb
εμε
δα
μεε
αδ
εε
αθ
εμε
μεε
εε
+
+
++
+=
+
++
)(
(4)
Easley (2008) indicated that, the daily trading data
contains important information about the order
arrival rate of informed traders and uninformed
traders (Easley, 2008). We set
T
T
as the total
number of trades per day, then the expected value of
the total trades is
][TTE
, which is the sum of the
Poisson arrival rate of informed traders and
uninformed traders.
The arrival rate of the buy order is
bbbb
BE
εδαμεαμεδααδε
+=+++= )-1()-1())(-1(][
the arrival rate of the sale order is
s
SSS
khh
khhSE
εαμδ
εαεδαμεαδ
++=
++++=
))-1((
)-1()-1()])-1(([][
and the expected value of the total trades is
sb
sb
khh
khhTTE
εεδδαμ
εεδαμαμδ
++−+−+=
++−+−+=
]1))1(([
)1())1((][
The expected value of the trade imbalance
BSK -=
, when
sb
ε
ε
=
A more informative quantity is the absolute value
of the trade imbalance. The first-order term of this
expectation relates directly to the arrival of the
informed trades
]-1))-1(([
)-1())-1((][
δδαμ
δαμαμδ
++=
++=
khh
khhKE
The expect balance order
K
T
T
-
is
=)-( KTTE
sb
ε
ε
+
It is clear from the above equation that, after
h
and
k
are introduced, the unbalanced order
K
include the arrival information of informed traders,
while the balance order
K
T
T
-
contains the arrival
information of uninformed traders, which is
consistent with Easley (2008) (Easley, 2008).
The calculation of PIN value needs to know the
trade direction. The most commonly used method to
judge the trade direction is the method proposed by
Lee and Ready (1991) (Lee, 1991). However, the
accuracy of this method has always been questioned
by scholars. Some scholars believe that the inaccurate
judgment of the trade direction will lead to the
underestimation of PIN. Therefore, in order to reduce
the unnecessary errors in the calculation process, we
use the high frequency data with trade direction to
conduct our empirical test.
3 MODEL VA L I D I T Y TEST
3.1 Samples and Data
Due to the China’s stock market crash in June, 2015
(Wu, 2016), stocks price illegitimately limited up and
limited down affected by other external factors,
during which the transaction data were at abnormal
level. Therefore, we abandon samples during that
period, and limit our sample time interval from 2011
to 2014. Learning from Karpoff (2010) (Karpoff,
2010) and considering the reliability of event source,
we selected those two types of bad news: (1) Listed
companies which had poor performance in the annual
report during 2012 and 2014. (2) Listed companies
which was punished by CSRC during Jan, 2012 and
March, 2015 due to the following reasons: short-term
trading, illegal disclosure, major accident and
connected transaction.
Because time points of the selected events are
dispersed, we use the multi-object asynchronous
event study method in this paper. By taking the
disclosure day as the benchmark, and recording it as
the event date, this is, the day 0, we set the estimation
window start from 100 days to 11 days before the
event day, denoted as [-100, -11]. The event window
is 10 days before and after the event day, denoted as
[-10, 10]. This is to say, sample stocks must have 100
consecutive trading days before the event day and 10
consecutive trading days after the event day. In order
to ensure the validity of the data and eliminate
abnormal samples, we also eliminated the ST, PT
stocks, and finally got 208 stocks, of which there are
ICPDI 2022 - International Conference on Public Management, Digital Economy and Internet Technology
140
67 stocks chose from type (1), and 141 stocks chose
from type (2).
We choose our sample stocks from Shenzhen A-
share market and Shanghai A-share market, and get
our microscopic characteristics data from CSMAR
database and RESSET database, and get our high-
frequency trading data from Giant Financial
Platform.
We break the tick-by-tick transaction data into 5-
minute data. The reasons are: on the one hand, private
information integrating into the data needs trading for
a certain time, the 5-minute data accumulates the
information containing in the tick-by-tick data. On
the other hand, the computation amount required by
the tick-by-tick data is too large, and it is easy to
overflow during the parameter estimation process,
resulting in false value.
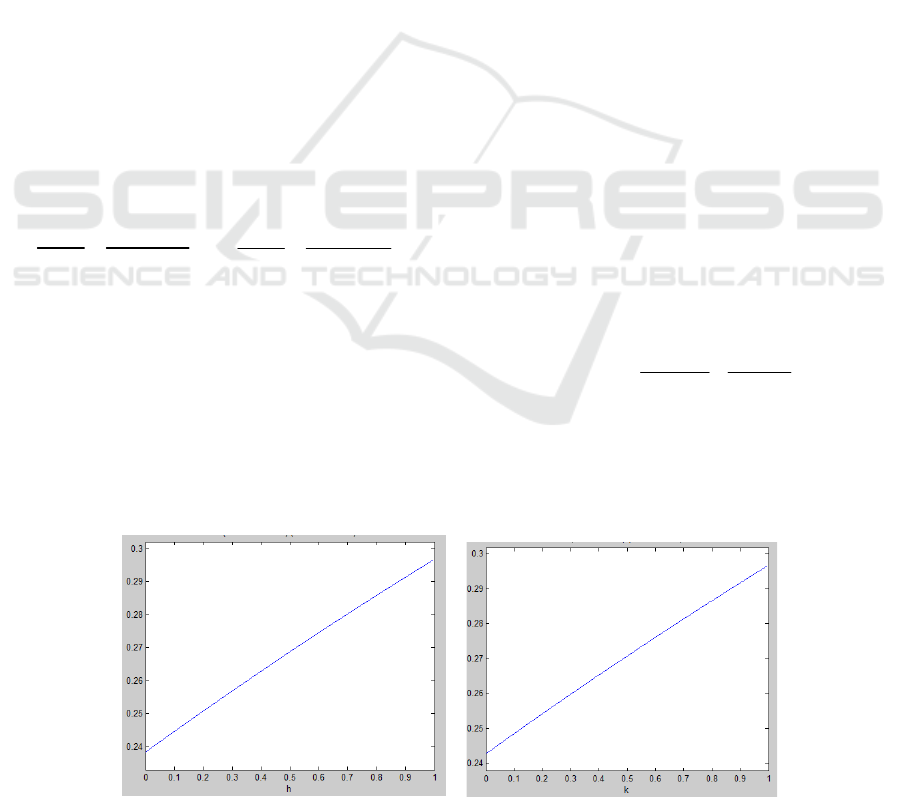
3.2 Parameters Sensitivity Analysis
We add two new parameters h and k in our SC-TPIN
model. In order to clarify the relationship between the
two parameters and SCTPIN, we make the following
sensitivity analysis: Firstly, we find the partial
derivative of PIN respect to h and k respectively by
formula derivation, to analyse the relationship
between PIN with h and k at [0, 1]. The partial
derivative of PIN respect to h and k are as follow:
2
)( BAh
AC
h
PIN
+
=
∂
∂
2
)( FDk
DC
k
PIN
+
=
∂
∂
Where
)1( kA
−=
α
μδ
,
sb
kB
ε
ε
α
μδ
α
μ
α
μδ
++−+=
,
sb
C
ε
ε
+=
,
)1( hD
−=
α
μδ
,
sb
hF
ε
ε
α
μδ
α
μ
α
μδ
++−+=
, and
A, B, C, D, and F are all greater than or equal to 0.
We can see that when h and k changes at [0, 1],
0/ >∂∂ hPIN
, and
0/ >∂∂ kPIN
, so PIN is the
increasing function of h and k respectively, and PIN
get its maximum and minimum when
1=h
(
1=k
)
and
0=h
(
0=k
). We use the figure to display the
change of SCTPIN when h and k change at [0, 1]
intuitively. As shown by figure 2.
The horizontal axis in figure 2 represent the
values of h and k at [0, 1], and the vertical axis
represents the change of SCTPIN. After we fixe other
values, the relationship between h and PIN presents
the form of inverse proportional function, when h
changes at [0, 1], the value of the PIN presents
positive and approximate linear form in figure 2, this
is, PIN is a strictly increasing function when h
changes at [0, 1]. The relationship between k and PIN
is approximately the same as that of h.
3.3 Model Validity Verification
Bid-ask spread is a common method used to measure
the information asymmetry between informed and
uninformed traders (O'hara, 2007). Reference to the
method used by Easley (1996) (Easley, 1996) and Qin
Lei (2005) (Lei, 2005), we verify the contribution our
SC-TPIN model in explaining asymmetric
information by measuring the explanatory power of
SCTPIN to the spread, which also can verify the
rationality of our SC-TPIN model apply to China's
stock market. Because China's stock market is the
order-driven market, it lacks corresponding bid-ask
spread data. Based on the availability of data and
acceptance of calculation method by scholars, we
choose the trading spread with volume suggested by
Stoll (2000) (Stoll, 2000) to calculate stocks’ spread.
The equation of the trading spread with volume
TSW
is as follows:
−
=
=
=
=
=
m
1j
m
1j
s
i
n
1i
n
1i
B
i
P
P
S
i
s
i
B
i
B
i
Q
Q
Q
Q
TSW
(5)
Where
B
i
P
and
S
j
P
are the price of the
i
th buy
and sell in unit time respectively,
B
i
Q
and
S
i
Q
are
corresponding volume respectively. The unit time is
Figure 2: The sensitivity analysis of h and k.
The Research of Probability of Informed Trading under Short-Sell Constraints
141

Table 1: Regression results for equation (6).
Independent variable Opening spread Closing spread Average spread
VSCTPIN
0.001817
(5.0499)***
0.001027
(5.6804)***
0.000825
(3.3543)***
VTPIN
0.001524
(4.1844)***
0.000115
(0.6280)
0.001002
(4.0258)***
VOL
0.001948
(3.0735)**
-0.000229
(-0.7192)
-0.001182
(-2.7288)**
R- squared 0.170043 0.084857 0.108927
Note: when the significance level is
α
=0.1, Z = 1.645; when
α
=0.05, Z = 1.96; when
α
=0.01, z=2.33; when
α
=0.001, Z = 3.29.
5 minute.
For the trading spread, we follow the method used
by Easley (1996) (Easley, 1996) and Qin Lei (2005)
(Lei, 2005), and select the opening spread, closing
spread and average spread as the dependent variable
respectively. After removing missing and invalid
data, we get the 5 minute opening spread (excluding
the call auction data), the 5 minute closing spread
(excluding the call auction data) and the average
spread (the average value of 5 minute spread per
trading day) of 187 sample stocks.
3.3.1 The Explanatory Power of SCTPINs
Consistent with Easley (1996) (Easley, 1996) and Qin
Lei (2005) (Lei, 2005), we use the panel regression
(6) to test the explanatory power of SCTPINs:
tititititi
VOLVTPINVSCTPIN
,,3,2,10,
ε
β
β
β
β
++++=Σ
(6)
Here
ti,
is the spread, VSCTPIN is the product
of SCTPIN and stock price, VTPIN is the product of
TPIN and stock price, VOL is the trading volume
defined as the product of stock price and share
volume,
ε
is the residual, and
]1,10[ −−∈t
. Existing
researches show that the probability of informed
trading has a positive effect on the spread, and VOL
has a negative effect on the spread (Li, 2010), so the
expected coefficient of VOL is negative. As
competing measures of information asymmetry,
VTPIN and VSCTPIN are expected to have positive
coefficients. If one of the two measures completely
subsumes the other in explaining spread, then we
expect to see a significant positive coefficient for the
dominant measure and an insignificant one for the
other. The regression results of equation (6) are
shown in Table 1, and the brackets are the values of
t-statistic.
As can be seen from Table 1, the regression
coefficient of VOL is significant when explaining the
opening spread and the average spread, and the
regression coefficient is negative when explaining the
average spread. The coefficient is negative when
explaining the closing spread, but it is not significant.
The coefficient of VTPIN is significant in explaining
the opening spread and the average spread, but it
can’t explain the closing spread. VSCTPIN has
significant explanatory power for all three spreads,
and its regression coefficients are all positive,
especially when explain the opening spread and the
closing spread, the coefficients of VSCTPIN are
larger than that of VTPIN. Since the sample mean of
VSCTPIN is larger than VTPIN, the overall
explanatory power of VSCTPIN is higher than that of
VTPIN (Lei, 2005).
3.3.2 The Predictive Power of SCTPINs
In order to test whether the SCTPINs is more
informative than other measures of information
asymmetry, we run the following panel regression to
compare the predictive power of these measures for
predicting the spread of the next trading day.
1,6,5,4
,3,2,101,
+
+
++++
+++=Σ
tititi
titititi
MERVOLOIMB
VOLVTPINVSCTPIN
εβββ
ββββ
(7)
1, +
ti
refers to the next day's trading spread,
VSCTPIN is the product of SCTPIN and stock price,
VTPIN is the product of TPIN and stock price, VOL
is the trading volume defined as the product of stock
price and share volume, OIMB is the order imbalance
or absolute net order flow in number of trades, as the
events we selected are the bad events, the OIMB here
equal to daily sell trades minus daily buy trades. ME
is the market value of equity, and RVOL is the
volatility of returns. Chordia et al. (2002) argue that
order imbalances reduce liquidity, so the predicted
sign for absolute order imbalance is positive
(Chordia, 2002), that is, the coefficients of
VSCTPIN, VTPIN, and OIMB should be positive.
Stocks with large market cap generally have good
liquidity, so the coefficient of ME is expected to be
negative. Inventory theory holds that stocks with
large earning volatility tend to have large spread
ICPDI 2022 - International Conference on Public Management, Digital Economy and Internet Technology
142
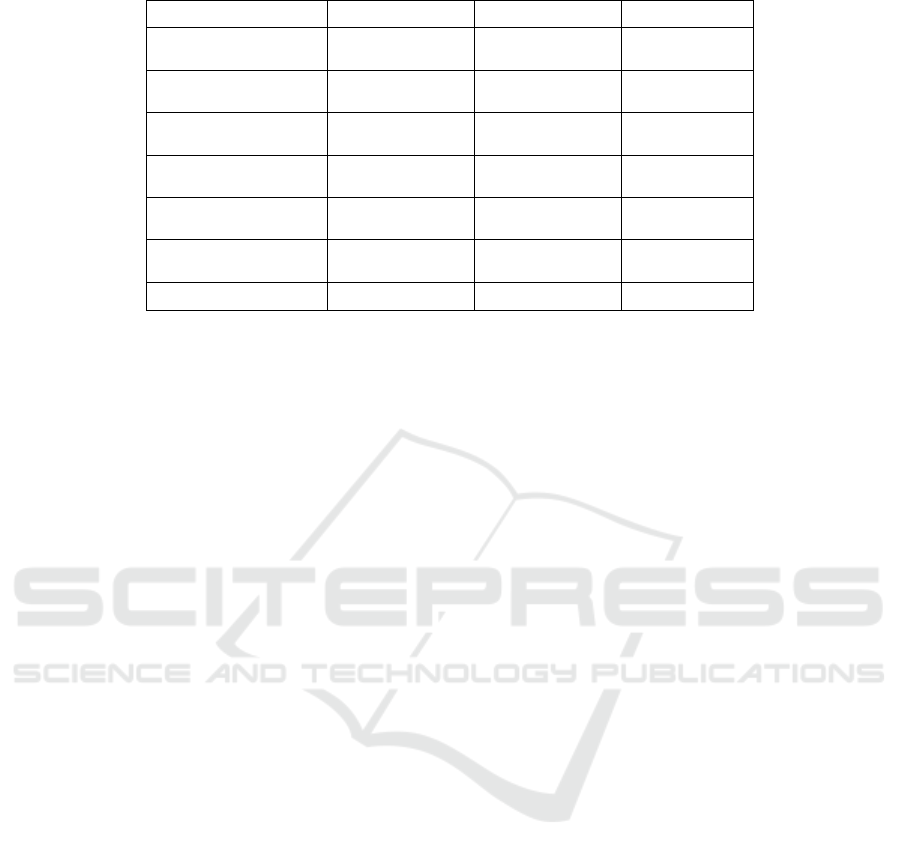
Table 2: The regression results of equation (7).
Independent variable Opening spread Closing spread Average spread
VSCTPIN
0.002189
(
6.066
)
***
0.000839
(
4.6845
)
***
0.000964
(
3.9971
)
***
VTPIN
0.001442
(3.9179)***
0.000278
(1.5303)
0.000927
(3.7821)***
VOL
0.003491
(
4.5418
)
***
0.000218
(
0.5720
)
-0.000907
(
-1.7655
)
*
RVOL 0.037095
(
1.1571
)
-0.030371
(
-1.9084
)
*
0.026972
(
1.2584
)
OMBI 6.90E-09
(0.5175)
-2.84E-09
(-0.4296)
-4.16E-09
(-0.4671)
ME -0.002089
(-2.3631)**
-0.000563
(-1.2839)
-0.000895
(-1.5147)
squaredR −
0.200612 0.081735 0.120732
Note: when the significance level is
α
=0.1, Z = 1.645; when
α
=0.05, Z = 1.96; when
α
=0.01, z=2.33; when
α
=0.001, Z = 3.29.
(Lei,.2005), so the expected sign for RVOL is
positive. The regression results of equation (7) are
shown in table 2
As can be seen from table 2, the regression
coefficients of VSCTPIN are all positive and
significant when explaining the opening spread, the
average spread, and the closing spread, indicating that
VSCTPIN has significant explanatory power for all
three spreads of one day after. VTPIN has significant
explanatory power for the opening spread and the
average spread, but its explanatory power for the
closing spread is 0. Meanwhile, the regression
coefficients of VTPIN are smaller than that of
VSCTPIN. VOL has significant explanatory power
for the opening spread and the average spread, but the
coefficient is negative only when explaining the
average spread. For other variables, only the
coefficient of RVOL and ME are significant when
explaining the closing spread and the opening spread
respectively. So we believe that SCTPIN is a better
and more robust measure in predicting future spreads,
even after controlling for other competing measures
of information asymmetry.
From the results above, we can see that, compared
with TPIN, SCTPIN has strong explanatory power in
explaining the same time series spreads and strong
predictive power in forecasting future spreads,
indicating that our SCTPIN model has strong power
in explaining the information asymmetry in China’s
stock market, so our SC-TPIN model is effective.
4 CONCLUSIONS
The classic models of the probability of informed
trading set no limitation on short selling based on
private information, while it has short-sell constraints
in present China’s stock market, which could result
in measurement deviation when applying the classic
models to China's stock market directly. In this paper,
we develop a SC-TPIN model by incorporating two
short-sell constraint variables into the classical
model, and select eligible sample stocks to verify it.
By parametric characteristics analysis, order flow
information analysis, and explanatory and predictive
power test in explaining trading spreads, we prove
that our SC-TPIN model is valid, and can better
estimate the probability of informed trading of stocks
with bad events in China’s stock market.
By analyzing the time characteristics of the results
of our SC-TPIN model, we found that stocks with
high pre-event PIN value have significantly higher
PIN value before the event day than that after the
event day, while stocks with low pre-event PIN value
have no significant difference before and after the
event day, indicating that stocks with higher PIN
value are more likely to be informed traded before
bad news disclosure.
Through analyzing the microscopic
characteristics of the results of our SC-TPIN model,
we find that stocks with high institutional ownership,
low turnover, small market cap, small securities
lending scale and low price characteristics have
higher probability of informed trading, and informed
traders tends to short stocks with large volume and
low institutional ownership when bad event arrives.
In addition, compared with TPIN model, our SC-
TPIN model has stronger explanatory power in
explaining the same time series spread and stronger
predictive power in forecasting future spread.
Our model can be used to provide reference for
securities regulators investigating insider trading
timely, and it can also provide a relatively reliable
way for uninformed traders avoiding stocks with bad
The Research of Probability of Informed Trading under Short-Sell Constraints
143

events. However, our model does not consider the
interaction between different types of traders, which
could be suggested as the research direction in future.
ACKNOWLEDGMENT
This research is the achievement of Shenzhen
Humanities and Social Sciences Key Research Base.
REFERENCES
Chordia T, Roll R, Subrahmanyam A. Order imbalance,
liquidity, and market returns. Journal of Financial
Economics 2002, 65: 111–130.
Duarte J, Young L. Why is PIN priced? Journal of Financial
Economics, 2009, 91(2): 119-138.
Easley D, Kiefer N, O'Hara M, Paperman J B. Liquidity,
Information, and Infrequently Traded Stocks. Journal of
Finance, 1996, 51(4):1405-1436.
Easley D, Engle R F, O'Hara M, Wu L. Time-Varying
Arrival Rates of Informed and Uninformed Trades.
Journal of Financial Economics, 2008, 6(2): 171-207.
Guo H, Wang C F, Fang Z M. Influence of Information
Asymmetry on Liquidity in View of Short-sale
Constraint in A-share’s Market. Journal of Xidian
University (Social Science Edition), 2013, 23(2): 47-54.
Karpoff J M, Lou X X. Short Sellers and Financial
Misconduct. The Journal of Finance, 2010, 65(5): 1879-
1973.
Lei Q, Wu G J. Time-varying Informed and Uninformed
Trading Activities. Journal of Financial Markets, 2005,
8: 153-181.
Lee C, Ready M J. Inferring Trade Direction from Intraday
Data. The Journal of Finance, 1991, 46(2): 733-746.
Li G C, Liu S C, Qiu W H. The probability of informed
trading in continuous order driven market: A new
method. Journal of Management Sciences in China,
2010, 13(10): 8-20.
O'Hara M. Market microstructure theory. Blackwell
Publishers, London, 1997:
Stoll H. Presidential address: friction. Journal of Finance,
2000, (4): 1479-1514.
Wang C F, Guo H, Fang Z M. Research on update of A-
share’s trade arrival rate and innovation digestion in the
perspective of high-frequency data. Management
Review, 2013, 25(8): 32-38.
Wu X Q. Stock Market Crisis: Structural Defects and
Regulatory Reform. Finance & trade economics, 2016,
(1): 22-32.
Xie H B, Fan K K, Zhou M. A study on the difference
between the reactions of Chinese stock market to good
and bad news. System Engineering Theory and
Practice, 2015, 35(7): 1777-1783.
Yang Z S, Yao S Y. An Empirical Study on the Spread and
Information Based Trading of the Shanghai Stock
Exchange. Journal of Financial Research, 2004, (4): 45-
56.
Yuan H Y. Short selling Mechanism and Operation
Performance of China’s Securities Market. Economic
Science Press, 2011: 38-39.
ICPDI 2022 - International Conference on Public Management, Digital Economy and Internet Technology
144
