
Neural Network Interpretation of Bayesian Logical-Probabilistic
Fuzzy Inference Model
Gulnara I. Kozhomberdieva
1a
, Dmitry P. Burakov
2b
and Georgii A. Khamchichev
1c
1
Department of Information and Computing Systems, Emperor Alexander I St. Petersburg State Transport University,
Moskovsky pr., 9, Saint Petersburg, 190031, Russia
2
Department of Information Technology and IT Security, Emperor Alexander I St. Petersburg State Transport University,
Moskovsky pr., 9, Saint Petersburg, 190031, Russia
Keywords: Artificial Neural Network, Multilayer Neural Network, Fuzzy Neural Network, Neuro-Fuzzy Network, Fuzzy
Inference, Fuzzy Logic, Bayesian Logical-Probabilistic Model of Fuzzy Inference, Bayesian Approach,
Probabilistic Logic, Bayes’ Theorem.
Abstract: The paper discusses the possibilities of using the Bayesian logical-probabilistic model of fuzzy inference,
previously proposed, researched and software implemented by the authors, in a neural network context. A
multilayer structure of a neuro-fuzzy network based on a Bayesian logic-probabilistic model is presented.
According to the authors, the proposed network structure is comparable to the well-known Takagi–Sugeno–
Kang and Wang–Mendel neuro-fuzzy networks. An example shows which network parameters can be used
to train it.
1 INTRODUCTION
Currently, the world is experiencing another wave of
neural networks popularity as the most dynamically
developing area in the field of artificial intelligence.
Impressive achievements in this area are primarily
associated with the rapid increase in computing
power and the emergence of super-large data sets
used to train artificial neural networks.
The previous wave of interest to neural network
technologies in artificial intelligence, during the
1990s and 2000s, was marked by successful attempts
to hybridize intelligent information processing
systems (especially in automatic control and
regulation systems), combine the advantages of fuzzy
inference systems and neural networks in the so-
called fuzzy neural (hybrid) networks (Yarushkina,
2004; Rutkovskaya et al., 2013; Osovsky, 2018).
The effectiveness of the neural network apparatus
is determined by their approximating ability, due to
which neural networks are universal functional
approximators capable of implementing any
continuous functional dependence based on training.
a
https://orcid.org/0000-0002-5499-8473
b
https://orcid.org/0000-0001-7488-1689
c
https://orcid.org/0000-0002-6747-8514
At the same time, the disadvantages of neural
networks include the inability to explain the output
result, because the knowledge accumulated by the
network are distributed among neurons in the form of
weight coefficient values.
Systems with fuzzy logic are deprived of this
drawback; however, already at the stage of their
design, there are required expert knowledge about the
method of solving the problem of control or
regulation, the formulation of rules, and membership
functions. Therefore, there is no possibility to train
such systems.
The combination of neural network and fuzzy
approaches in hybrid systems allows, on the one
hand, to bring the training ability and the parallelism
of calculations that are inherent to neural networks to
fuzzy inference systems. On the other hand, it allows
to strengthen the intellectual capabilities of neural
networks by linguistically interpretable fuzzy
decision-making rules (Yarushkina, 2004;
Rutkovskaya et al., 2013; Souza, 2020).
At that, there are distinguished two types of
hybrids: neuro-fuzzy networks (NFN) and fuzzy
50
Kozhomberdieva, G., Burakov, D. and Khamchichev, G.
Neural Network Interpretation of Bayesian Logical-Probabilistic Fuzzy Inference Model.
DOI: 10.5220/0011901700003612
In Proceedings of the 3rd International Symposium on Automation, Information and Computing (ISAIC 2022), pages 50-56
ISBN: 978-989-758-622-4; ISSN: 2975-9463
Copyright
c
2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

neural networks (FNN). Hybrid fuzzy neural
networks (FNN) are networks (similar to the
structures of classical neural networks) based on
fuzzy neurons with fuzzy inputs and outputs and/or
fuzzy weights. Neuro-fuzzy networks (NFN) can be
defined as multilayer neuro-network fuzzy systems
that use a fuzzy rule base to calculate the output signal
and provide the ability to adaptively adjust the
parameter values fed to the parametric layers.
In the overview article (Souza, 2020) as well as in
the works (Sinha and Fieguth, 2006; Wu et al., 2020;
Kordestani et al., 2019; Siddikov et al., 2020; Zheng
et al., 2021; Fei et al., 2021; Manikandan and
Bharathi, 2017; Caliskan et al., 2020; Chertilin and
Ivchenko, 2020; Vassilyev et al., 2020), the numerous
examples of both types of hybrid networks usage are
presented, that indicates the relevance and intensity of
modern research and development in this field.
The paper discusses the possibility of using a
Bayesian logic-probabilistic model (BLP model) of
fuzzy inference in the structure of a multilayer neuro-
fuzzy network (NFN). The model was proposed
(Kozhomberdieva, 2019) at the International
Conference on Soft Computing and Measurement
(SCM’2019, St. Petersburg, Russia), researched and
software implemented by the authors of this report
(Kozhomberdieva and Burakov, 2019;
Kozhomberdieva and Burakov, 2020;
Kozhomberdieva et al., 2021). A demonstration
example of solving the problem of fuzzy inference is
given. The example shows which network parameters
can be used to train it. According to the authors, the
proposed network structure is comparable to the well-
known Takagi–Sugeno–Kang and Wang–Mendel
neuro-fuzzy networks (Osovsky, 2018).
2 NEURO-FUZZY NETWORK
BASED ON THE BAYESIAN
LOGICAL-PROBABILISTIC
MODEL
Let us give a brief description of the BLP fuzzy
inference model proposed and described in details by
the authors in (Kozhomberdieva, 2019;
Kozhomberdieva and Burakov, 2019;
Kozhomberdieva and Burakov, 2020;
Kozhomberdieva et al., 2021). The BLP fuzzy
inference model is based on the use of probabilistic
logic and the Bayes’ Theorem when performing fuzzy
inference according to a scheme similar to the well-
known Mamdani model.
The original principle of the BLP model is the
transformation of the base of fuzzy rules represented
by the Boolean functions (BF) into a set of
probabilistic logic functions (PLF). The PLF
arguments are the membership functions values of the
input linguistic variables (LV) terms and the
calculated values are used as conditional probabilities
𝑃
𝑒
|
𝐻
, 𝑘=1,…,𝐾, which determine the
correspondence degrees of the values set of the input
variables 𝑥
,…,𝑥
(“crisp” evidence) to assumptions
about the truth of the Bayesian hypotheses 𝐻
,…,𝐻
,
corresponding to the values set of the output LV. The
conditional probabilities are used to determine the
posterior Bayesian probability distribution 𝑃
𝐻
|
𝑒
,
𝑘=1,…,𝐾 on a set of hypotheses. The resulting
posterior probability distribution is used at the final
stage of fuzzy inference – when defuzzifying the
value of the output LV.
We note an important feature of the BLP model –
the requirement that the number of fuzzy rules and the
number of terms of the output LV, which determines
the set size of the Bayesian hypotheses, coincide. If
necessary, the set of rules is reduced by combining all
rules with the same conclusion into one fuzzy rule.
The combined rule is a disjunction of antecedents of
the combined rules, and the combined rule weight is
defined as the arithmetic mean of the combined rules
weights.
To go from representations of fuzzy rules in the
BF form to their representations in the PLF form,
Boolean functions are transformed to orthogonal
(ODNF) or perfect (PDNF) disjunctive normal form.
The rules for the formal transition from the BF that
specified in the PDNF or ODNF to the corresponding
PLF are following (Ryabinin, 2015):
1) logical variables 𝑧
,𝑧
,…,𝑧
are replaced
with the corresponding probabilities 𝑝
,𝑝
,…,𝑝
;
2) instead of negations 𝑧
, 1−𝑝
are used;
3) conjunctions and disjunctions are replaced
with arithmetic multiplication and addition,
respectively.
The posterior probability distribution on the set of
hypotheses is calculated by an equation based on the
Bayes’ Theorem equation:
𝑃
𝐻
|
𝑒
=
∙
𝑒
𝐻
∑
∙
𝑒
𝐻
, (1)
where 𝐾 is the number of Bayesian hypotheses
(output LV terms) equals to the number of PLF used
to evaluate the truth degree of evidence in favor of
each hypothesis, 𝑤
is the weight of the 𝑘-th rule,
𝑤
∈
0, 1
. In the equation (1), there are no prior
probabilities used in the classical Bayes’ Theorem
equation, since in the context of fuzzy inference, the
prior probability distribution on the set of hypotheses
is assumed to be uniform (the hypotheses are equally
probable).
Neural Network Interpretation of Bayesian Logical-Probabilistic Fuzzy Inference Model
51
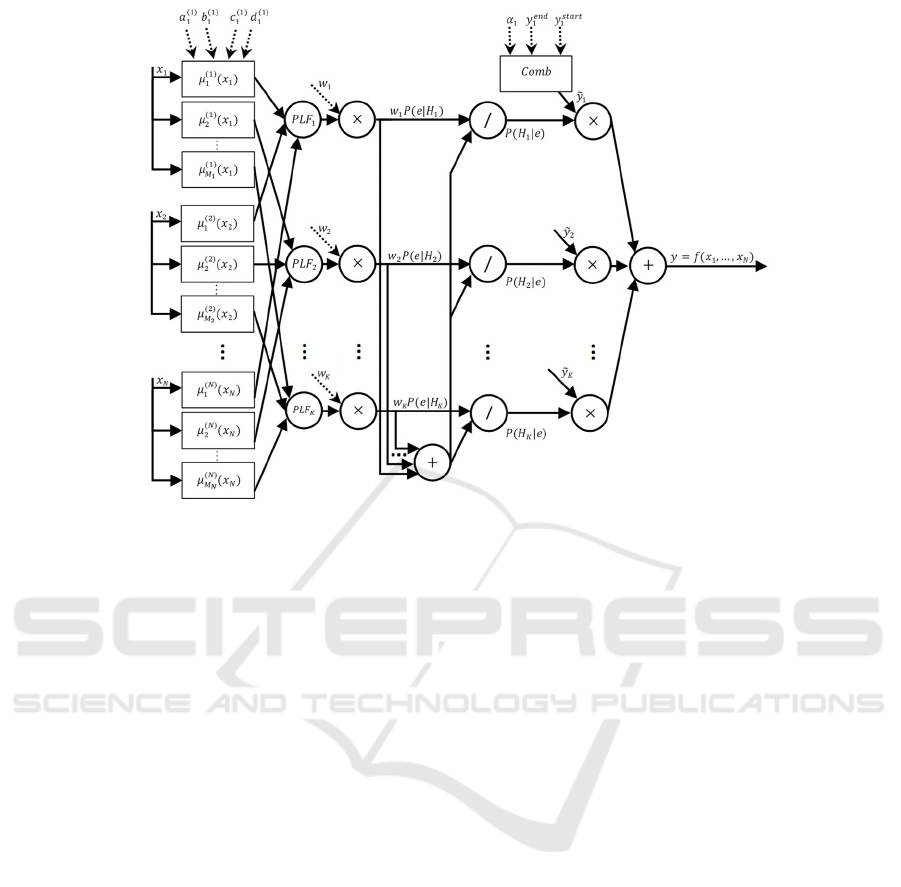
Figure 1: Structure of a neuro-fuzzy network based on a BLP model.
During defuzzification, the final value of the
output variable 𝑦 is determined as the mathematical
expectation (average value) of a discrete random
variable 𝑦:
𝑦=𝑀
𝑦
=
∑
𝑦
∙𝑃
𝐻
|
𝑒
, (2)
where 𝑃
𝐻
|
𝑒
is the 𝑘-th element of the posterior
probability distribution calculated by the equation (1),
and 𝑦
is the characteristic value of the corresponding
𝑘-th term of the output LV, which is by default taken
as the central point of the interval on which this term
is defined.
Figure 1 shows the structure of a neuro-fuzzy
network based on the BLP model, the neurons of
which perform the operations necessary to calculate
the value of some output function 𝑦=𝑓𝑥
,…,𝑥
using a set of input variable values 𝑥
,…,𝑥
. The
network has seven layers:
• the first (parametric) layer performs separate
fuzzification of each input variable, determining
the membership function values for each fuzzy
rule. In order to simplify the figure, the parameters
to be adapted within the network training process
are schematically indicated in Figure 1 only for
the trapezoidal membership function 𝜇
𝑥
,
further used in the example in paragraph 3;
• the second (non-parametric) layer calculates,
basing on a set of rules transformed into a PLF set,
the conditional probabilities values 𝑃
𝑒
|
𝐻
,
𝑘=1,…,𝐾. Depending on the task solved by the
neuro-fuzzy network, the fuzzy rule base can be
either formed by an expert, or (in the absence of
linguistic information) is generated using a well-
known universal algorithm for constructing a
fuzzy rule base based on numerical data (Wang
and Mendel, 1992; Rutkovskaya et al., 2013);
• the third (parametric) layer multiplies the results
obtained from the second layer on the weight
coefficients of the fuzzy rules 𝑤
∈
0, 1
, which
can be used as parameters within the network
training process;
• the fourth (non-parametric) layer consists of a
single adder neuron that calculates the sum of the
weighted conditional probabilities 𝑃
𝑒
|
𝐻
,
𝑘=1,…,𝐾, given from the third layer;
• the fifth (non-parametric) layer consists of
neurons that perform the division operation in
accordance with the equation (1) to obtain
posterior Bayesian probability distribution
𝑃
𝐻
|
𝑒
, 𝑘=1,…,𝐾, on the set of hypotheses
that the output LV has some assigned value from
its term-set;
• the sixth (parametric) layer consists of neurons
each of that multiplies the probability 𝑃
𝐻
|
𝑒
,
𝑘=1,…,𝐾 on the corresponding characteristic
value 𝑦
of the output LV term. To calculate the
characteristic value, a convex combination of two
boundary points 𝑦
and 𝑦
of the
corresponding interval of the output variable scale
is applied. The combination coefficient
0, 1
ISAIC 2022 - International Symposium on Automation, Information and Computing
52
defines the shift of the characteristic value of the
term within the interval. Parameters 𝑦
, 𝑦
and
are the network settings, the use of which
is shown in the example in paragraph 3;
• the seventh (non-parametric) layer consists of a
neuron-adder that generates the final value of the
output variable 𝑦=𝑓𝑥
,…,𝑥
in accordance
with the equation (2).
3 EXAMPLE OF SOLVING THE
PROBLEM AND SETTING UP
THE NEURO-FUZZY
NETWORK
As an explanatory example, we use the well-known
demonstration problem “Dinner for Two”, which,
despite the simplicity of the solution, completely
allows the authors to show the possibilities of using a
neuro-fuzzy network based on the BLP model as a
universal approximator of continuous functional
dependence based on training.
Let it be necessary to develop an expert system to
determine the tips amount to be left to the waiter of the
establishment, depending on the level of service and
the ordered dishes cooking quality. The visitor
estimates the service and food quality on a 10-point
scale, and the amount of tips paid – as a percentage
(from 0 to 25% of the cost of dinner). This fuzzy
model is included in the MATLAB demo examples
(https://www.mathworks.com/help/fuzzy/fuzzy-
inference-process.html), but in this paper it is
presented in the edition used by the authors earlier in
(Kozhomberdieva, 2019; Kozhomberdieva and
Burakov, 2019; Kozhomberdieva and Burakov,
2020).
In the fuzzy inference system, the corresponding
LVs for the estimated indicators Service and Food are
formulated, the membership functions of their terms
are defined on the indicator scales, and a system of
fuzzy rules is formed that uses statements about the
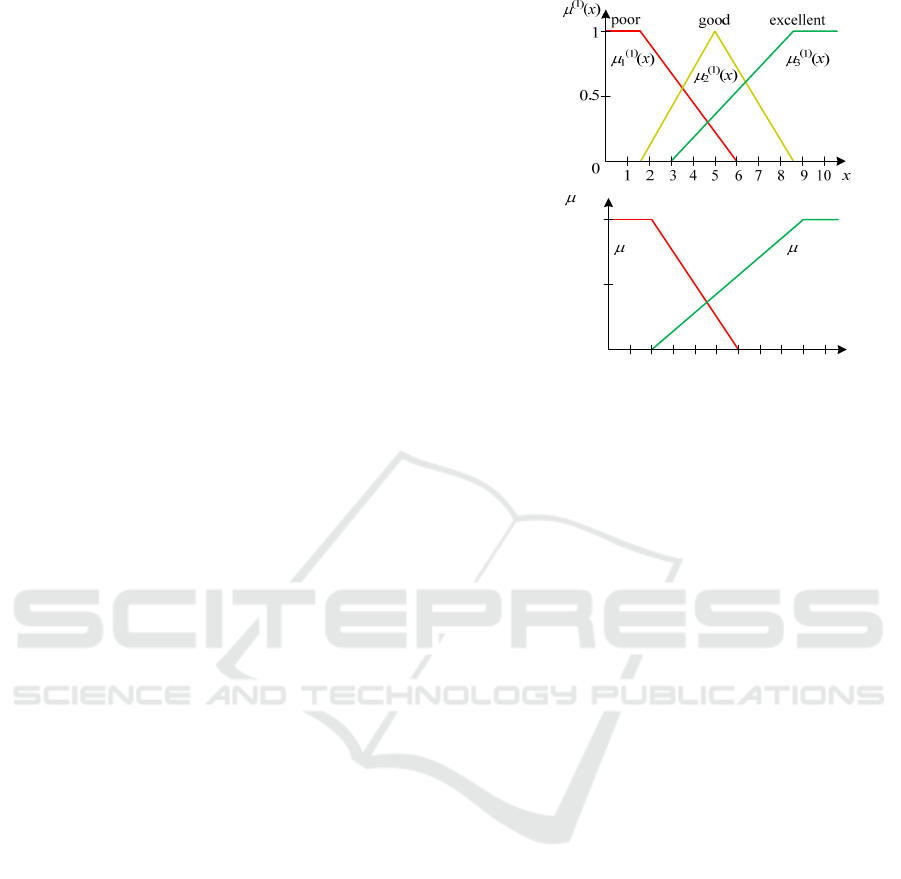
LV values in antecedents and conclusions. Graphs of
the membership functions of the input LVs are shown
in Figure 2.
The scale of the output variable Tip, in accordance
with the conditions of the problem, is divided into
three non-overlapping intervals [0, 5], [5, 20],
[20, 25], corresponding to the linguistic values
“small”, “average” and “big”, respectively. Note that
the definition of membership functions for the terms
of the output LV in a neuro-fuzzy network based on
the BLP model is not required.
Figure 2: Membership functions 𝜇
𝑥 of input LV terms.
The following fuzzy rules are used:
1) IF Service is “poor” OR Food is “rancid”
THEN Tip is “small”;
2) IF Service is “good” THEN Tip is “average”;
3) IF Service is “excellent” AND Food is
“delicious” THEN Tip is “big”.
These rules are firstly presented as BFs, specified
in the PDNF, and then transformed into a set of PLF.
Obtained probabilistic functions are used to calculate
conditional probabilities that estimate the degree to
which a set of values of input variables 𝑥
, and 𝑥
(“crisp” evidence) fits the assumptions about the truth
of Bayesian hypotheses about the value (“small”,
“average”, or “big”) of the output LV:
𝑃
𝑒
|
𝐻
=𝜇
𝑥
𝜇
𝑥
−𝜇
𝑥
∙𝜇
𝑥
,
𝑃
𝑒
|
𝐻
=𝜇
𝑥
,
𝑃
𝑒
|
𝐻
=𝜇
𝑥
∙𝜇
𝑥
.
For example, in the calculations we use the input
values of the quality of service and food estimates
𝑥
=𝑥
=5. Let us set all the fuzzy rules weights 𝑤
equal to 1, and as the characteristic values of the
output LV terms, we will take by default the average
value of the boundary points corresponding to the
terms of the intervals 𝑦
and 𝑦
on the output
variable scale. Then, for given membership functions
(see Fig. 2), the posterior Bayesian probability
distribution
𝑃
𝐻
|
𝑒
,𝑘=1,2,3, calculated by the
equation (1) will be represented by the set of values
0.26, 0.64, 0.10
, and the desired tip size according
to the equation (2) will be 𝑦 = 11%.
Let us transform the fuzzy inference system built
to solve the “Dinner for Two” problem using the BLP
model into a neuro-fuzzy network, the structure of
which
corresponds to the network structure in
(2)
(x)
1
0.5
0
1 2 3 4 5 6 7 8 9 10 x
1
(2)
(x)
2
(2)
(x)
rancid delicious
Service
F
ood
Neural Network Interpretation of Bayesian Logical-Probabilistic Fuzzy Inference Model
53

(a) (
b
)
Figure 3: Surface plot of the output function 𝑦=𝑓𝑥
,𝑥
. a) – the values of the parameters are presented in Table 1, b) –
the values of the parameters are presented in Table 2.
Figure 1. Recall that the network is trained by
changing the parameters on the parametric layers, and
specify which parameters are used:
1. The membership functions 𝜇
𝑥
of the
input LV terms are trapezoids described by four
parameters 𝑎
,𝑏
,𝑐
,𝑑
, which are the x-
coordinates of the vertices of the trapezoids on the
membership functions graphs (the triangular
membership function is considered as a special case
of the trapezoidal, when 𝑏
= 𝑐
);
2. Weight coefficients of fuzzy rules 𝑤
∈
0, 1
(by default they are taken equal to 1);
3. Boundary points of the intervals 𝑦
and
𝑦
corresponding to the terms of the output LV on
the output variable scale, as well as the bias
coefficients of the characteristic value for each term
0, 1 (by default they are taken equal to 0.5).
The characteristic value of the term 𝑦
used in the
equation (2) is calculated as a convex combination of
boundary points:
𝑦
=
1−𝛼
∙𝑦
𝛼
∙𝑦
. (3)
Table 1: Example 1 of configuring network settings.
Inpu
t
LV Service Foo
d
Terms Poo
r
Goo
d
Excell. Rancid Delicious
Parameters of the membership functions and their values
a
j
(i)
0 1.5 3 0 2
b
j
(i)
0 5 8.5 0 9
c
j
(i)
1.5 5 10 2 10
d
j
(i)
6 8.5 10 6 10
Weights of fuzzy rules
w
k
1 1 1
Outpu
t
LV Tip
Terms Small Average Big
Parameters of terms output LV and their values
y
k
start
05 20
α
k
0.5 0.5 0.5
y
k
end
520 25
y = f(5, 5) = 11%
To demonstrate the possibilities of parameters
setting up a neuro-fuzzy network based on the BLP
model, Table 1 shows the values of the parameters
and the result of calculating the value of the output
function 𝑦=𝑓𝑥
,𝑥
for the example considered
above, and Table 2 – for the example with changed
network parameters.
Table 2: Example 2 of configuring network settings.
Inpu
t
LV Service Foo
d
Terms Poo
r
Goo
d
Excell. Rancid Delicious
Parameters of the membership functions and their values
a
j
(i)
0 1 7 0 2
b
j
(i)
0 4 9 0 9
c
j
(i)
14 10 5 10
d
j
(i)
49 10 9 10
Weights of fuzzy rules
w
k
0.75 1 0.5
Outpu
t
LV Tip
Terms Small Average Big
Parameters of terms output LV and their values
y
k
start
05 20
α
k
0 0.5 1
y
k
end
520 25
y = f(5, 5) = 6.5%
Figures 3.a and 3.b show plots of the resulting
surfaces, which differ markedly from each other.
ISAIC 2022 - International Symposium on Automation, Information and Computing
54

4 CONCLUSIONS
Numerous examples of the use of neuro-fuzzy
networks in automatic control and regulation systems
published in open sources testify to the relevance and
intensity of modern research and development in this
field.
The paper presents the structure of a neuro-fuzzy
network based on the BLP model of fuzzy inference,
previously proposed, researched and software
implemented by the authors. An example shows
which network parameters can be used to train it.
According to the authors, the proposed seven-
layer network structure with three parametric layers
is comparable to the well-known Takagi–Sugeno–
Kang and Wang–Mendel neuro-fuzzy networks.
When choosing an appropriate fuzzy rule base at
the stage of network building and then training it, a
network based on a BLP model can be used as a
universal approximator of a continuous functional
dependence. The authors plan to continue research in
this direction.
REFERENCES
Caliskan, A., Cil, Z. A., Badem, H., Karaboga, D. (2020).
Regression based neuro-fuzzy network trained by ABC
algorithm for high-density impulse noise elimination.
IEEE Transactions on Fuzzy Systems. 28(6):1084–
1095.
Chertilin, K. E., Ivchenko, V. D. (2020). Configuring
adaptive PID-controllers of the automatic speed control
system of the GTE. Russian Technological Journal,
8(6):143–156 (in Russian).
Fei, J., Wang, Z., Liang, X., Feng, Z., Xue Y. (2021).
Fractional sliding mode control for micro gyroscope
based on multilayer recurrent fuzzy neural network.
IEEE Transactions on Fuzzy Systems, 30(6):1712–
1721.
Kordestani, M., Rezamand, M., Carriveau, R., Ting, D. S.,
Saif, M. (2019). Failure diagnosis of wind turbine
bearing using feature extraction and a neuro-fuzzy
inference system (ANFIS). In Proc. Int. Work-Conf.
Artif. Neural Netw., pp. 545–556.
Kozhomberdieva, G. I. (2019). Bayesian logical-
probabilistic model of fuzzy inference.
Mezhdunarodnaya konferentsiya po myagkim
vychisleniyam i izmereniyam [International
Conference on Soft Computing and Measurements].
1:35–38 (in Russian).
Kozhomberdieva, G. I., Burakov, D. P. (2019). Bayesian
logical-probabilistic model of fuzzy inference: stages of
conclusions obtaining and defuzzification. Fuzzy
Systems and Soft Computing. 14(2):92–110 (in
Russian).
Kozhomberdieva, G. I., Burakov, D. P. (2020). Combining
Bayesian and logical-probabilistic approaches for fuzzy
inference systems implementation. Journal of Physics:
Conference Series. Volume 1703, 012042.
Kozhomberdieva, G. I., Burakov, D. P., Khamchichev, G.
A. (2021). Decision-Making Support Software Tools
Based on Original Authoring Bayesian Probabilistic
Models. Journal of Physics: Conference Series.
Volume 2224, 012116.
Manikandan, T., Bharathi, N. (2017). Hybrid neuro-fuzzy
system for prediction of stages of lung cancer based on
the observed symptom values. Biomedical Research,
28:588–593.
Osovsky, S. (2018) Neural networks for information
processing, trans. from Polish. by I. D. Rudinsky
[Neironnye seti dlya obrabotki informacii, per. s pol'sk.
I. D. Rudinskogo], Goryachaya Liniya – Telekom.
Moscow, 2
nd
edition, 448 p. (in Russian).
Rutkovskaya, D., Pilinsky, M., Rutkovsky, L. (2013).
Neural networks, genetic algorithms and fuzzy systems:
trans. from Polish. by I. D. Rudinsky [Neironnye seti,
geneticheskie algoritmy i nechetkie sistemy, per. s
pol'sk. I. D. Rudinskogo], Goryachaya Liniya –
Telekom. Moscow, 2
nd
edition, 384 p. (in Russian).
Ryabinin, I. A. (2015). Logical probabilistic analysis and its
history. International Journal of Risk Assessment and
Management, 18(3-4):256–265.
Siddikov, I. X., Umurzakova, D. M., Bakhrieva, H. A.
(2020). Adaptive system of fuzzy-logical regulation by
temperature mode of a drum boiler. IIUM Engineering
Journal, 21(1):185–192.
Sinha, S. K., Fieguth, P. W. (2006). Neuro-Fuzzy Network
for the Classification of Buried Pipe Defects.
Automation in Construction, 15:73–83.
Souza, P. V. C. (2020). Fuzzy neural networks and neuro-
fuzzy networks: A review the main techniques and
applications used in the literature. Appl. Soft Comput.
92, 106275.
Vassilyev S. N., Pashchenko F. F., Durgaryan I. S.,
Pashchenko A. F., Kudinov Y. I., Kelina A. Y.,
Kudinov I. Y. (2020). Intelligent Control Systems and
Fuzzy Controllers. I. Fuzzy Models, Logical-Linguistic
and Analytical Regulators. Automation and Remote
Control, 81(1): 171–191.
Vassilyev S. N., Pashchenko F. F., Durgaryan I. S.,
Pashchenko A. F., Kudinov Y. I., Kelina A. Y.,
Kudinov I. Y. (2020). Intelligent Control Systems and
Fuzzy Controllers. II. Trained Fuzzy Controllers, Fuzzy
PID Controllers. Automation and Remote Control,
81(1):922–934.
Wang, L. X., Mendel, J. M. (1992). Generating Fuzzy Rules
by Learning from Examples. IEEE Transactions on
Systems, Man, and Cybernetics, November/December
1992, 22(6):1414–1427.
Wu, X., Han, H., Liu, Z., Qiao, J. (2020). Data-knowledge-
based fuzzy neural network for nonlinear system
identification. IEEE Transactions on Fuzzy Systems,
28(9):2209–2221.
Yarushkina, N. G. (2004). Fundamentals of the theory of
fuzzy and hybrid systems [Osnovy teorii nechetkikh i
Neural Network Interpretation of Bayesian Logical-Probabilistic Fuzzy Inference Model
55

gibridnykh system], Finansy i statistika. Moscow, 320
p. (in Russian).
Zheng, K., Zhang, Q., Hu, Y., Wu, B. (2021). Design of
fuzzy system-fuzzy neural network-backstepping
control for complex robot system, Information
Sciences, 546:1230–1255.
ISAIC 2022 - International Symposium on Automation, Information and Computing
56
