Line Structured Light Measurement System, Method and

Experiments for Rail Profile

Qingli Luo

, Shubin Zhang and Zhiyuan Chen

State Key Laboratory of Precision Measuring Technology and Instruments, Tianjin

University, No. 92, Weijin Road, Nankai District, Tianjin 300072, China

Keywords: Line Structured Light, Profile Measurement, Light Plane Calibration, Center Line Extraction.

Abstract: More than 40,000 kilometers of high-speed railway has been built in China, and it is the longest all over the

world. The wear of railway rails would affect the safety of train operation. The traditional manual contact

measurement methods had the disadvantages of low measurement efficiency and the surface of the

measured object was easy to wear. Then, it was of great significance to develop high-precision, non-contact

rail profile measurement methods. This paper designed and implemented a method for rail profile

measurement with line-structured light. A structured light plane parallel to the cross-section of the rail was

emitted by a line laser. The image data were collected by an industrial camera, and then the actual rail

profile was extracted through the center line extraction algorithm and coordinate transformation. The

method has been tested on 60kg rail profile measurement and the profile measurement experiment results

proved it has higher precision and faster speed, compared with results from the Coordinate Measuring

Machine (CMM).

1 INTRODUCTION

In recent years, high-speed railways construction in

China has developed rapidly and the total operating

mileage has exceeded 40,000 kilometers. The high-

speed railway network spans north-south and east-

west, connecting different cities closely. It greatly

meets the travel needs of people and promotes

economic development of passing regions and plays

an increasingly important role in social development

(Ye, 2018). As an important part of the railway

system, rail is in direct contact with the train. Severe

wear, corrosion, fracture, peeling and other defects

will lead to serious safety accidents. Therefore,

regular inspection of rails is required. Since the rail

profile directly reflects the degree of rail defects and

represents the contact condition between wheel and

rail, it is necessary to measure the profile of the rail

section precisely, and then the data can provide a

scientific reference for rail maintenance (Wang et

al., 2018).

The traditional rail profile measurement

technology mainly depends on measurement tools

including mechanical rail wear rulers for contact

measurement (Zhang, 2019). Contact measurement

requires the participation of inspection personnel,

with the disadvantages of a low degree of

automation, low testing efficiency, and poor real-

time performance, and then it cannot meet the

requirements of high-speed railway development

(Zhou et al., 2020). Moreover, the contact

measurement requires contact with the rail surface,

and it will wear instruments, affect the measurement

accuracy and damage the surface of the rail (Wu et

al., 2020).

By contrast, in the iterative updating process of

the computer and electronic technology, the non-

contact measurement methods depending on optical

means have attracted more attention. They are

categorized into passive and active ways according

to imaging illumination modes. Passive

measurement builds a human-like binocular vision

system and it extracts distance information from two

different visual directions of a 2D image (Jiang et

al., 2020; Xu et al., 2019; Wang et al., 2019). The

disadvantages are heavy computing burden, low

precision, and slow calculation, and it is highly

dependent on the texture characteristics of the

measured objects. The active measurement relies on

structured light technology. Structured light is

categorized into three types based on the beam

emitted by the laser: point, line, and plane (Zhang,

162

Luo, Q., Zhang, S. and Chen, Z.

Line Structured Light Measurement System, Method and Experiments for Rail Proﬁle.

DOI: 10.5220/0011916900003612

In Proceedings of the 3rd International Symposium on Automation, Information and Computing (ISAIC 2022), pages 162-168

ISBN: 978-989-758-622-4; ISSN: 2975-9463

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

2018). The device of point structured light is simple.

However, the shortcomings are cumbersome and

time-consuming and not suitable for large-sized

objects (Cui, 2018). The surface structured light

increases the measurement range and processing

efficiency. And the disadvantages are increasing of

calibration complexity and data processing.

Moreover, since the measurement results are easily

affected by the other light sources and the reflection

performance of the object surface, it has higher

requirements for the measurement environment

conditions (Landmann et al., 2018). Compared with

the above two types of structured lights, line

structured light only uses the emitted light plane to

intersect the contour of the object for measurement.

The advantages are simple structure, fast image

processing speed, and little influence due to

environmental conditions, and it has good stability

in industrial applications (Lian et al., 2019). For

example, it is applied to measure the contour of the

disc cam (Hu, 2020) and to the detection system

(Ren, 2021).

This paper designed a monocular line structured

light rail profile measurement method with the

advantages of non-contact, high precision, and high

speed. The method first used a line laser to emit a

structured light plane parallel to the cross-section of

the rail, then collected image data through an

industrial camera, and finally obtained the actual rail

profile through a center line extraction algorithm and

coordinate transformation model. The method has

the characteristics of simple equipment and quick

processing.

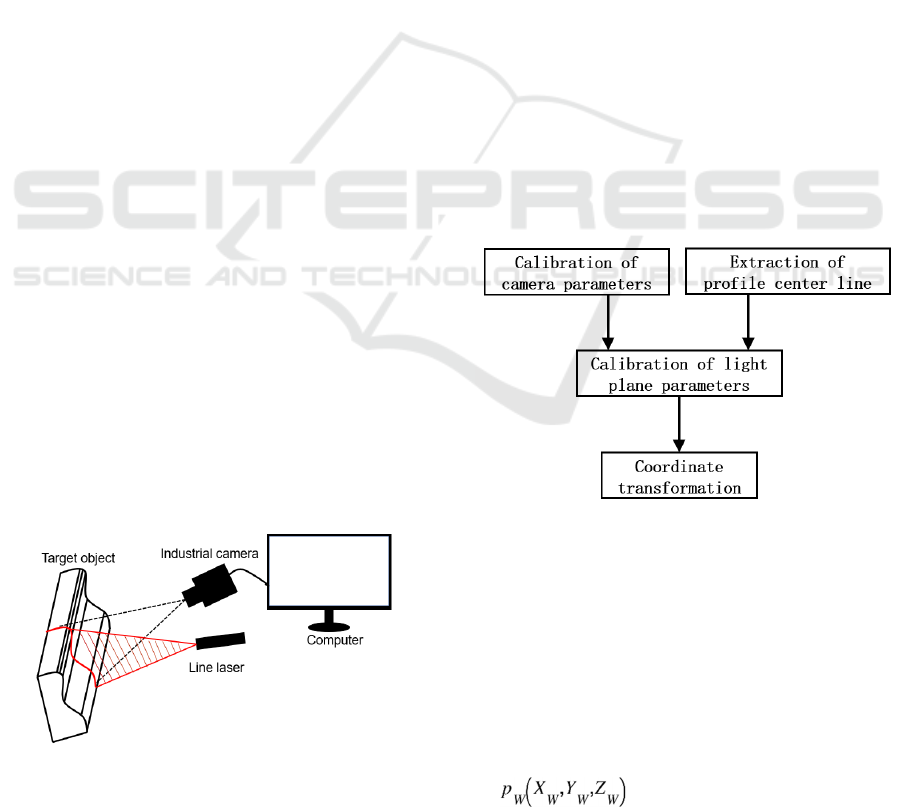
2 METHODOLOGY

In this paper, the monocular line structured light is

exploited to realize rail profile measurement. The

measurement system schematic diagram is shown in

figure 1. The main equipment includes an industrial

Figure 1: The schematic diagram of the measurement

system for the rail profile.

camera, a line laser, and a computer. The line laser

emits a structured light plane parallel to the cross-

section of the rail. It forms a structured light band

and then the rail profile information is captured on

the rail surface. The industrial camera and structured

light plane form a certain angle to capture the light

band image and then the image is transmitted to a

computer. The laser center line of the rail profile

image is processed by the corresponding algorithm

and the 2D image coordinates are transformed into

actual physical coordinates with the camera

calibration transformation model. The measurement

profile is finally obtained.

Figure 2 presents the flowchart of the

measurement system for rail profile and it consists

of four parts: calibration of camera parameters,

extraction of profile center line, calibration of light

plane parameters, and coordinate transformation.

The camera calibration is to obtain the mapping

relationship of the image coordinate, camera

coordinate, and world coordinate. The extraction of

the profile center line mainly realizes rail profile

extraction from the image. The calibration of the

light plane is applied to obtain coefficients of the

structured light plane and then applied for

subsequent restoration of the rail profile. The

coordinate transformation finishes transforming the

2D profile image into the actual measured profile of

the rail.

Figure 2: The flowchart of the measurement system.

2.1 Calibration of Camera Parameters

The camera parameters should be calibrated before

imaging. In our experiments, a 2D plane calibration

plate is applied to the camera calibration. The reason

is that a 2D target can provide more reliable

manufacturing accuracy and is easy to use,

compared with a 3D target.

The world coordinate of the point is represented

as , and the pixel coordinate is

Line Structured Light Measurement System, Method and Experiments for Rail Proﬁle

163

represented as . is the scale factor. H is the

camera's external parameter matrix and the internal

parameters under different spatial poses are

represented by matrix M. The camera calibration

transformation model is established as equation (1).

(1)

The parameters to be calibrated are listed in

Table 1. The horizontal and vertical scale factors of

the image are represented by and , the

coordinates of the main point of the image are

represented by and , and is the tilt factor. The

distortion parameters of the lens are represented by

vector K, and the radial and tangential distortion

coefficients are represented by and . The

rotation and translation matrix from camera

coordinates to world coordinates are represented by

R and T, which form the camera external parameter

matrix H.

Table 1: The calibration parameters of the camera.

Parameters

Expression

Perspective

transformation

matrix

Len distortion

arameter matrix

Rotation matrix

Translation vector

2.2 Extraction of Profile Center Line

An ideal structured light image consists of a constant

background and a uniform target light band. To

calculate the center points of the light band, it is

necessary to separate the background from the target

light band. However, the unavoidable existence of

noise in actual collected images comes from the

external environment and inside of the laser.

Complex object surface conditions and other factors

will bring difficulties to the extraction of the light

band, so some actions need to be taken to reduce

these bad effects. In this paper, the collected image

is pretreated by background processing, Gaussian

filtering, and grayscale segmentation. Then the

center point is extracted from the target light band

by the Steger algorithm. Finally, the image

coordinates are restored to real profile coordinates

through the line structured light measurement model.

In the step of background processing, two images

of the calibration plate are captured when the line

laser is working or non-working. These two images

are subtracted and then a structured light image with

a completely black background is calculated.

After background processing, Gaussian filtering

is applied. Gaussian kernel function takes the

weighted average results of the gray value of all

pixels in the neighborhood to be the gray value of

the central pixel. Different weights are set to pixels

at different positions and a higher weight is set when

the position is closer to the central pixel. Then, it has

the advantage that the gray distribution characteristic

of the image can be preserved as completely as

possible when reducing noise.

Following that, grayscale segmentation is

applied. The filtered image can be divided into the

light band and background based on the grayscale

feature. Assuming that the grayscale of any pixel of

the target image is , we set a threshold G, and

the pixels whose grayscale value is greater than G

belong to the foreground, otherwise, these pixels

belong to the background.

Then, the Steger algorithm is performed to obtain

the center line. It performs Taylor polynomial

expansion on the gray distribution of the light band

in the normal direction of each pixel and takes the

extreme point that satisfies both the polynomial and

second derivative of the gray level as the center

point of the light band. Compared with other center

extraction algorithms, the Steger algorithm has the

advantages of better processing accuracy and

robustness, and it fully considers the direction of the

light band.

According to Steger’s conclusion, of the

Gaussian kernel function should satisfy equation (2).

(2)

where w is half of the width of the light band and the

scale of the Gaussian kernel function is .

ISAIC 2022 - International Symposium on Automation, Information and Computing

164

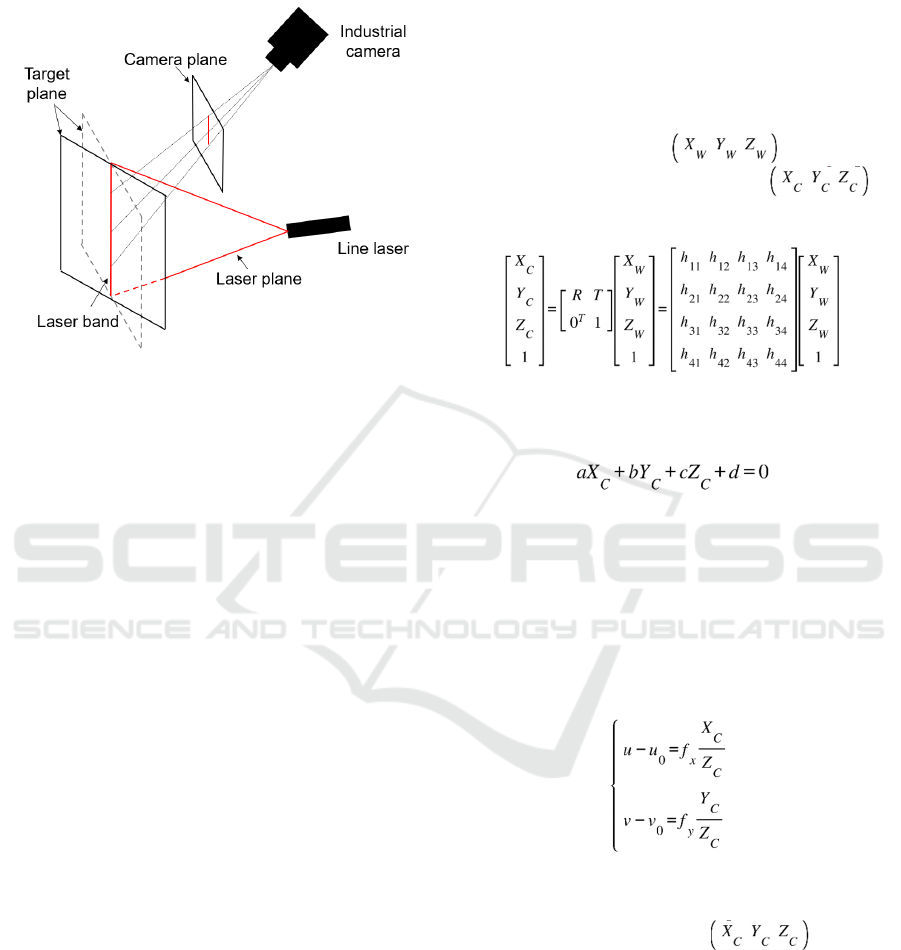
2.3 Calibration of Light Plane

Parameters

Figure 3. The model of laser plane calibration.

A 2D plane target is adopted in the calibration of the

light plane. First, take all points on the light band as

a set of calibration points. Second, by freely moving

the plane target within the measurement range of the

laser, the image coordinates of multiple sets of non-

collinear calibration points are obtained. Then

convert them into a camera coordinate system

according to the relationship between the target

plane and the image plane. Finally, the parameters of

the light plane are obtained by least squares fitting.

We use a 2D calibration plate. During the calibration

process, the calibration plate does not need to keep

parallel movement and can freely change position

and posture within the camera view, reducing the

difficulty of operation. There is no need to extract

calibration points. We convert all coordinates on the

light band to a world coordinate system, which

increases the number of calibration points, thereby

reducing the error of results.

The specific calibration process is as follows.

(1) The target position is adjusted to locate in the

center of the camera view and it is intersected with

the structured light plane.

(2) The laser switch is turned on and then the line

structured light is emitted to the 2D target. The

image is collected. Then the laser switch is turned

off without changing the position of the target.

Another image is collected.

(3) The position of the target is adjusted and the

above steps are repeated to obtain multiple sets of

target images and corresponding images with a

structured light band.

(4) After completing the above acquisition

process, the rotation and translation matrices are

calculated by using the perspective transformation

matrix M and the model in Section 2.1.

(5) The sub-pixel center points of laser bands of

targets with different poses are obtained through

image processing algorithms.

(6) Substitute the pixel coordinates of each

center point into equation (1) in Section 2.1 to

calculate its coordinates in target plane

world coordinates. The coordinates are

calculated by equation (3).

(3)

Finally, the light plane is fitted by the least

square method.

(4)

2.4 Coordinate Transformation

Coordinate transformation transforms the two-

dimensional pixel coordinates of the center points in

Section 2.2 into 3D coordinates of the actual rail

profile. It rotates the structured light plane to be

parallel to the coordinate plane, and the actual

profile curve is calculated.

(5)

Firstly, the two-dimensional pixel coordinates of

the rail profile are taken into equation (5) and three-

dimensional coordinates of the

measurement profile can be obtained with equation

(4) in Section 2.3.

Then, the camera coordinates are taken into

equation (8) to rotate around the x and y axes and

the rotation angle is determined by equations (6) and

(7).

Line Structured Light Measurement System, Method and Experiments for Rail Proﬁle

165

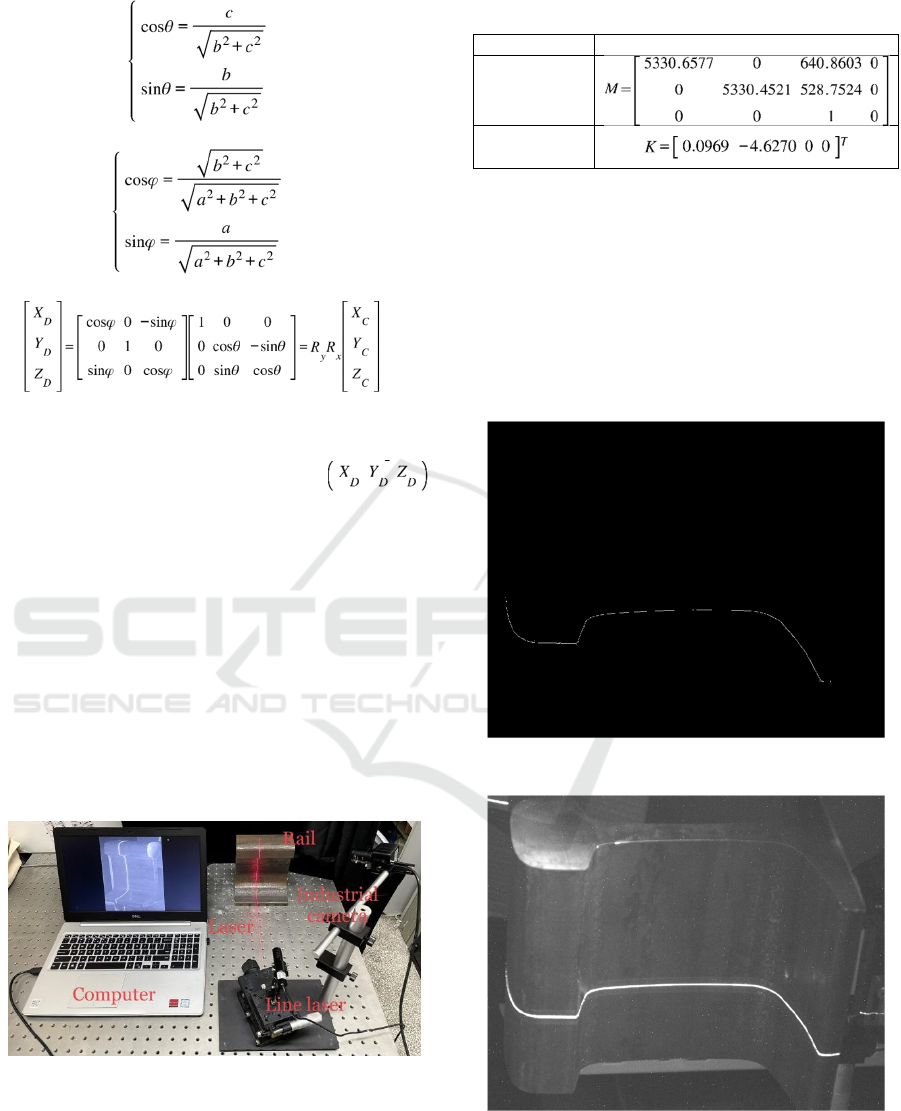
(6)

(7)

(8)

After coordinate transformation, the structured

light plane is rotated to be parallel to the XOY plane

and the actual rail profile coordinates

are extracted.

3 EXPERIMENTS AND RESULTS

The BFS-U3-13Y3M black and white area array

industrial camera and the Tamron M112FM25 low-

distortion industrial lens were used in the

experiments. A high-precision checkerboard

calibration board with 12x9 corner points was

selected and the cell size was 15x15mm. The

calibration toolbox Camera Calibrator was applied

to the industrial camera calibration in our

experiment.

Figure 4. Line structured light measurement system.

The calibration results of the camera are shown

in Table 2.

Table 2: The results of camera parameters calibration.

Parameters Value

Internal

parameters

Distortion

arameters

Figure 5(a) presents the line structured light

profile image of the 60Kg rail collected in a

laboratory environment and Figure 5(b) illustrated

the results after center line extraction. Figure 6

provides the visualization results of the center points

of the light band in the light plane transformed from

local world coordinate systems. The light plane is

fitted by the least square method and the values of

the parameters are shown in Table 3.

(a) Profile measurement of 60Kg rail.

(b) Center line of 60Kg rail.

Figure 5: Images of rail profile.

ISAIC 2022 - International Symposium on Automation, Information and Computing

166

Table 3: The fitting results of line structure light plane.

Parameters

a b c d

Value

0.1458 -1.4166 -1 962.7770

Figure 7(a) and (b) present the rail profile

results between the standard and our measured

profiles, and the results between the standard and

CMM measured profile, respectively.

Figure 6: Line structure light plane.

(a) The rail profile measured between the standard and our

measured profile.

(b)The rail profile measured between standard and

CMM measured profile.

Figure 7: The results of measurement.

To quantitatively evaluate the experimental

results, three different distance algorithms, including

Hausdorff Distance (HD), Frechet Distance (FD)

(Alt, 2009; Xie et al., 2017), and Dynamic Time

Warping Distance (DTWD) (Keogh et al., 2005)

were applied to calculate the fitting degree of rail

profile. As shown in Table 4, the results of these

distance algorithms proved that our system has

higher accuracy compared with CMM.

Table 4: The fit degree of the rail profile (Lower is better

for all distance algorithms).

Name FD HD DTWD

CMM 22.71 2.15 0.43

8.79 0.65 0.38

Our measurement method is composed of several

different techniques and which are photography,

optics, and image processing. The factors affecting

measurement error come mainly from two aspects:

hardware system and software algorithm.

The error in the hardware system comes from the

camera and laser. The camera is used for image

acquisition. Higher camera resolution results in less

distortion, better performance, higher quality

images, and more accurate measurement. The laser

is used to emit a line laser. The thinner and straighter

the laser is, the better quality of extracted center line

will be.

The error in the software algorithm comes from

calibration and image processing. The extraction

accuracy of calibration points has a great influence

on the final results. In our method, all points of the

light band are used to fit to reduce the error.

Moreover, the extraction accuracy of center points is

greatly affected by external noise, the performance

of the processing algorithm, and the state of the rail

Line Structured Light Measurement System, Method and Experiments for Rail Proﬁle

167

surface. The background processing algorithm

applied in this paper can reduce the errors during

processing.

4 CONCLUSION

This paper designed and implemented a method for

measuring the profile of rail with a monocular line

structured light system. We applied it to measure the

60kg rail profile and compared the results with that

from the CMM. The experiment proved that our

measurement results are as good as the CMM and

our method has higher measurement efficiency

compared with the point-by-point contact

measurement of CMM. The experiments were

completed in a static environment in the laboratory,

and further research should focus on profile

measurement under outdoor dynamic conditions.

ACKNOWLEDGMENTS

We would like to thank the support from Dr. Peng

Wang and Dr. Ji Deng for building the system and

data calibration. This research was supported by

National Engineering Laboratory for Digital

Construction and Evaluation Technology of Urban

Rail Transit (grant No. 2021ZH04).

REFERENCES

Ye, H. (2018). Research on key technologies of automatic

3D measurement of high speed railway hub based on

line laser scanning. Master’s thesis, HUST.

Wang, H., Li, Y., Ma, Z., Zeng, J., Jin, T., and Liu, H.

(2018). Distortion rectifying for dynamically

measuring rail profile based on self-calibration of

multiline structured light. In IEEE Transactions on

Instrumentation and Measurement, pages 678-689.

IEEE.

Zhang, Z. (2019). Research on the rail wear measurement

system based on machine vision. Master’s thesis,

BJTU.

Zhou, Z., Yang, H., and Liu, J. (2020). Research on the

three-dimensional detection system of the rail full

profile. In Journal of Physics: Conference Series,

1633(1): 012002.

Wu, F., Dou, H., Wu, Y., Li, Z., and Yang, X. (2020).

Method for detecting sharp rail contour based on

machine vision. In Optical Technique, 46(04): 453-

460.

Jiang, Y., Wang, Z., Han, J., Jin, Y., and Li, B. (2020).

Regional fuzzy binocular stereo matching algorithm

based on global correlation coding for 3D

measurement of rail surface. In Optik, 207: 164488.

Xu, G., Chen, J., Li, X., and Su, J. (2019). Profile

measurement adopting binocular active vision with

normalization object of vector orthogonality. In

Scientific Reports, 9(1): 1-13.

Wang, P., Li, W., Li, B., and Li, B. (2019). Structured-

light binocular vision system for dynamic

measurement of rail wear. In 2019 IEEE 2nd

International Conference on Electronics Technology

(ICET), pages 547-551. IEEE.

Zhang, S. (2018). High-speed 3D shape measurement with

structured light methods: A review. In Optics and

Lasers in Engineering, 106: 119-131.

Cui, H., Hu, Q., and Mao, Q. (2018). Real-time geometric

parameter measurement of high-speed railway

fastener based on point cloud from structured light

sensors. In Sensors, 18(11): 3675.

Landmann, M., Heist, S., Brahm, A., Schindwolf, S.,

Kühmstedt, P., and Notni, G. (2018). 3D shape

measurement by thermal fringe projection:

optimization of infrared (IR) projection parameters. In

Dimensional Optical Metrology and Inspection for

Practical Applications VII, 10667: 9-18.

Lian, F., Tan, Q., and Liu, S. (2019). Block thickness

measurement of using the structured light Vision. In

International Journal of Pattern Recognition and

Artificial Intelligence, 33(01): 1955001.

Hu, Z. (2020). Research on vision measurement

technology of disc cam based on line structure light.

Master’s thesis, JLU.

Ren, J. (2021). Based on line structured light of

pantograph slide abrasion detection system research.

Master’s thesis, NYCU.

Alt, H. (2009). The computational geometry of comparing

shapes. In Efficient Algorithms. pages 235-248.

Xie, D., Li, F., and Phillips, J, M. (2017). Distributed

trajectory similarity search. In Proceedings of the

VLDB Endowment, 10(11): 1478-1489.

Keogh, E., Ratanamahatana, C, A. (2005). Exact indexing

of dynamic time warping. Knowledge and information

systems, 7(3): 358-386.

ISAIC 2022 - International Symposium on Automation, Information and Computing

168