Application of Wavelet Analysis to Correlation Between Sunspot

Activity and Precipitation in Yunnan Province

Siyuan Du and Zhongmu Li

Institute of Astronomy, Dali University, Dali, 671003, China

Keywords: Wavelet Analysis, Correlation Analysis, Sunspot Numbers, Precipitation.

Abstract: Wavelet analysis is widely applied in the processing of time series such as climate and hydrology to extract

the change characteristics and periodic relations. Based on wavelet analysis and time lag correlation analysis,

this paper studies the correlation between sunspot numbers and precipitation at seven meteorological stations

in Yunnan Province from year 1959 to 2019.The results show that the cross wavelet analysis and time lag

correlation analysis are suitable for studying the periodic response and time delay relationship between solar

activity and climate factors. These two methods can extend to other geographical locations. It is shown that

the resonance period between sunspot numbers and the annual mean precipitation at the seven meteorological

stations are mainly concentrated in the scale of 8-12a, and there are obvious time lag relationships between

these time series from the phase angle. The time lag correlation analysis shows that there are different time

delays between sunspot numbers and precipitation in different climatic regions.

1 INTRODUCTION

As a powerful statistical tool, wavelet analysis has

been used in the field of mathematics for about a

century. It is a development of the Fourier Transform,

which can be used for time-frequency analysis of

signals with non-stationary characteristics. The

wavelet transform replaces the infinitely long

trigonometric basis in the Fourier transform with a

finite length decaying wavelet basis to obtain the

frequency change and time information. At present,

wavelet analysis is widely used in signal analysis,

image processing, quantum mechanics, theoretical

physics and other fields. Many scholars apply wavelet

analysis to climate analysis to diagnose the internal

hierarchy of climate change and analyze the evolution

characteristics of time series at different scales. For

example, Li and Gao et al. (2017) used wavelet

analysis to study the influence of solar activity and El

Nino on extreme precipitation in the Loess Plateau.

They found that the maximum precipitation mainly

occurred at or near the peak of sunspot numbers, and

extreme precipitation often occurred in the year after

El Nino event. Li and Wen et al. (2020) studied the

time response to drought based on the wavelet

transform method. They found that meteorological

drought and hydrological drought had obvious

periodicity on the scale of 2-4a, and hydrological

drought was usually followed by meteorological

drought for 1-2 months. Zhao and Luo (2021) applied

wavelet analysis to the study of temperature and

precipitation changes in Dabie Mountain in western

Anhui Province. The results showed that temperature

had an oscillation periodicity of 22a and 10a, and

precipitation had an oscillation periodicity of 26a. We

will get different conclusions by using wavelet

analysis to study climate characteristics at different

regions.

Climate changes have always been a hot issue of

social concern. The frequent occurrence of extreme

climates has caused huge losses to human life and

property. It will greatly reduce and avoid the harm

caused by climate changes if we understand the

climate changes, improve the accuracy of predictions

and take effective measures to cope with climate

change actively. At present, many scholars improve

the accuracy of climate prediction by data

assimilation, such as Cheng and Argaud et al. (2021)

use a flexible combination of existing covariance

tuning algorithms to tackle the problem of a

multivariate and spatially distributed hydrological

model and gain a significantly more accurate and

more robust flow forecast for the Tarn river. We can

also increase climate factors in the prediction model

to improve the accuracy. The climate changes are

224

Du, S. and Li, Z.

Application of Wavelet Analysis to Correlation Between Sunspot Activity and Precipitation in Yunnan Province.

DOI: 10.5220/0011918400003612

In Proceedings of the 3rd International Symposium on Automation, Information and Computing (ISAIC 2022), pages 224-229

ISBN: 978-989-758-622-4; ISSN: 2975-9463

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

influenced by many factors, such as solar activity,

atmospheric circulation, ENSO, land-sea distribution,

global warming and anthropogenic factors. Sunspots

are a symbol of solar activity. The sunspot numbers

are related to the intensity of solar radiation.

Therefore, this study uses sunspot numbers to

represent the solar activity to investigate the

correlation between solar activity and precipitation.

Based on the precipitation in Yunnan Province at

seven meteorological stations and sunspot numbers,

this paper adopts the method of wavelet analysis and

correlation analysis to study the possible relationship

between solar activity and precipitation. It helps for

analyzing the mechanism of solar activity affecting

climate change and predicting climate changes in

Yunnan Province.

2 MATERIALS AND METHOD

2.1 Study Area

Yunnan Province is located in the Yunnan-Kweichow

Plateau region, between latitudes within 21°8 ' N ~

29°15' N and longitudes within 97°31 ' E~106°11 ' E,

covering an area of 394100 km

. Due to the influence

of atmospheric circulation, there are different climate

zones in the province. The main climatic zones

including north tropical zone, South subtropical zone,

middle subtropical zone, North subtropical zone,

South humid zone, middle temperate zone and

plateau climate zone. The paper selects the

precipitation data of one meteorological station in

each of the 7 climatic zones for research. The 7

meteorological stations are Kunming Station, Pu'er

station, Mengla Station, Zhaotong Station, Gongshan

Station, Lijiang Station and Shangri-La Station.

Because of geographical complex topography and

diverse climate zones, it is important to select

precipitation data from different meteorological

stations in Yunnan Province to study the correlation

between solar activity and precipitation.

2.2 Data

The precipitation data of Yunnan Province are

selected from the National Meteorological Science

Data Center (https://data.cma.cn). The sunspots data

are selected from Royal Observatory of Belgium,

Brussels (https://www.sidc.be/silso/homes). The

study covers the period from year 1959 to 2019 (61

years). Even though there are some abnormal,

missing or invalid information exists in the original

data, it will not bring much influence on the result of

the research if these abnormal data are processed. In

this study, missing values are filled in and outliers are

replaced.

2.3 Method

2.3.1 Wavelet Analysis

Wavelet analysis is an effective method to reveal the

temporal structure time series (Wang & Wang, 1996).

Many time series show non-stationary in their

statistics. Different from most classical signal

analysis methods, wavelet analysis can be used to

detect and analyze the non-stationary of signals

(Chellali, Khellaf & Belouchrani, 2010). It can help

us extract the change features with complex temporal

patterns, such as periodic variation and response

events. Wavelet transform is a powerful time-

frequency analysis method, which has been applied in

many studies (e.g.,

Chellali, Khellaf & Belouchrani,

2010; Alperovich, Zheludev & Hayakawa, 2016).

These applications help to develop the wavelet

analysis theory and practice (Torrence &Webster,

2010; Ge, 2007). In this paper, we use cross wavelet

transform to analyze the respond periodicity of two

time series. Cross wavelet transform is constructed by

continuous wavelet transform to study their high-

power region and phase relationship in the time-

frequency interval. Continuous wavelet transform is

an important method widely used in wavelet analysis.

Here, Morlet wavelet is used as the wavelet basis

function of continuous wavelet transform and it is

defined as follow.

In equation (1),

is the frequency parameter.

we often choose

6=ω

because it can make the

balance between time and frequency. t is the time

parameter.

The continuous wavelet is a band-pass filter

which can be stretched and translated to get different

wavelet basis. The continuous wavelet transform of

wavelet

is defined as.

In equation (2),

)t(x

is the input data. t is the time

parameter. s is the scale parameters (inversely

proportional to the spatial frequency).

is the

2/t

4/1

ee)t(

−

π=ψ

(1)



τ−

ψ=τψ= dt)

()t(x

)s,(CWT

(2)

Application of Wavelet Analysis to Correlation Between Sunspot Activity and Precipitation in Yunnan Province

225

position offset.

*ψ

represent the complex conjugate

of the function

Cross wavelet transform is used to analyze the

correlation between two time series in the time-

frequency domain (Banerjee & Mitra, 2014). The

cross wavelet transform can reveal the similarity or

difference between time series, quantify the

correlation and the lag relationship between two time

series. The cross wavelet transform of two time series

and

is defined as.

W.W=W

(3)

In equation (3),

is the wavelet coefficient

matrix of time series

is the wavelet

coefficient matrix of time series

is the

complex conjugate matrix of wavelet coefficient

matrix

. The larger value of

|W|

is, the more

significant the correlation is. It means that there is a

common high energy region between two time series.

The cross wavelet transform uses the phase angle

to estimate the phase difference of two time series. It

can represent the lag relationship between two time

series.

)

)}s(W{r

)}s(W{i

arctan(

neal

nmag

(4)

In equation (4),

eal

represents the real part of the

cross wavelet coefficient.

mag

i represents the

imaginary part of the cross wavelet coefficient.

According to the relationship between phase angle

and period, phase lead or lag can be obtained. In the

cross wavelet transform power spectrum figure (as

shown in figure 1). ← indicates that sunspots are

negative correlated with precipitation. → indicates

that they are positive correlated. ↓ indicates that

sunspots lead precipitation by 90°. ↑ indicates that

sunspots lag precipitation by 90°. In figure 1, red and

blue colors represent the peak and valley values of

energy density. It reflects the local and dynamic

characteristics of the time-frequency transformation

of the dominant fluctuation. The shades of color

represent the relative change of energy density. Thick

solid black line is the 5% significance level, which

has passed the red noise test. Thin solid black line

denotes the boundary of wavelet influence cone. This

area is the edge effect of wavelet transform which

cannot be ignored (Grinsted, Moore & Jevrejeva,

2004).

2.3.2 Time Lag Correlation Analysis

In the study of atmospheric, ocean and other scientific

problems, the response of the process is often not

immediate. It is necessary to carry out time lag

correlation analysis on the time series. Time lag

correlation analysis is to determine whether there is a

certain correlation between two time series if one

time series is lagged a period of time. The way to do

that is letting the time series y

lags by the value from

-n to n, and then calculate its Pearson coefficient with

the other time series y

. It is assumed that the

correlation is strongest by the value of i. If i > 0 means

that y

lags y

by the value of i. If i <0, then y

is ahead

of y

by i.

Pearson's correlation coefficient was developed

by Carl Pearson. Pearson correlation analysis uses

Pearson's formula to obtain the correlation coefficient

r of two variables. The calculation formula of

correlation coefficient is.

Y,X

S.S

)Y,X(COV

(5)

In equation (5), r

X,Y

represents the correlation

coefficient between series X and series Y. COV(X,Y)

is the covariance between series X and series Y. S

and S

are the sample variances of series X and series

Y. The value of r

X,Y

ranges from -1 to 1, with a

positive value indicating a positive correlation and a

negative value indicating a negative correlation. The

larger value of |r

X,Y

|, the better the correlation

between two time series.

3 RESULT AND DISCUSSION

3.1 Result of Cross Wavelet Analysis

In this study, cross wavelet transform is used to

analyze the response relationship between sunspot

numbers and the average annual precipitation of

seven meteorological stations in Yunnan Province.

The cross wavelet power spectrum of the time series

are shown in Figure 1.

From the cross wavelet power spectrum, it can be

seen that sunspot numbers and the precipitation of

seven meteorological stations with different climates

in Yunnan Province have different scale periodic

response. They have significant characteristics in the

high-power region. Figure 1(a) shows cross wavelet

power spectrum of the sunspot numbers and average

ISAIC 2022 - International Symposium on Automation, Information and Computing

226

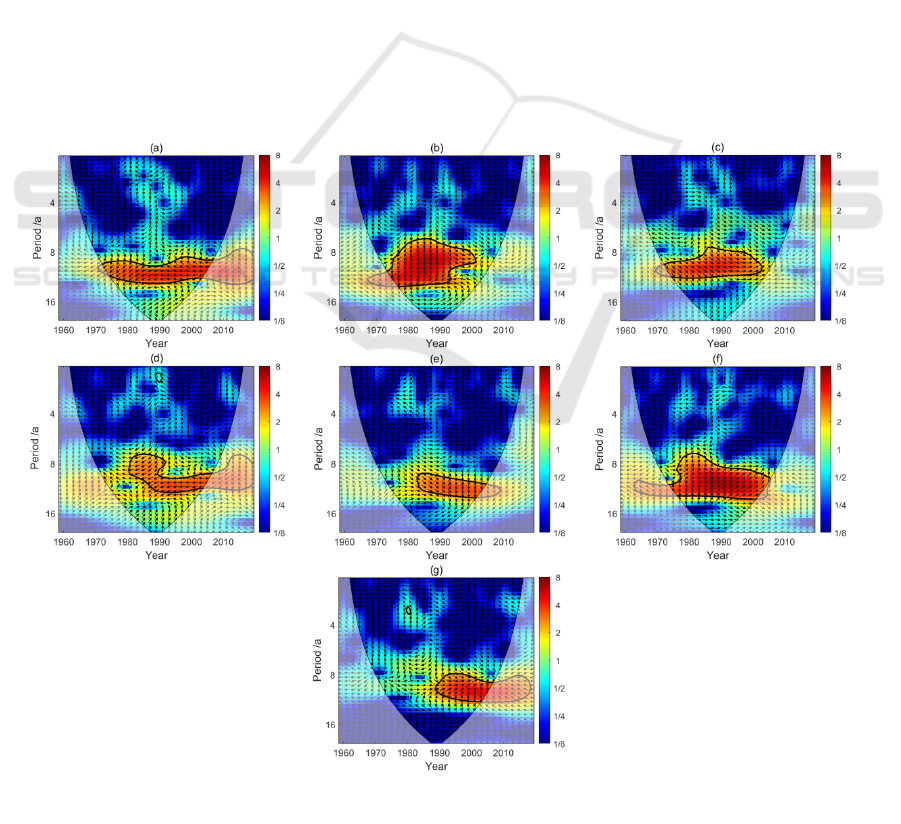
annual precipitation in kunming. We can see that

there is a 9-12a resonance period between sunspot

numbers and precipitation from year 1972 to 2007,

which shows a high power. The phase difference

indicates that the sunspot numbers and average

annual precipitation are negative correlated in

kunming. Figure 1(b) is the cross wavelet power

spectrum of the sunspot numbers and the average

annual precipitation of Pu’er. The resonance cycle of

sunspot numbers and precipitation is concentrated in

the scale of 8-12a from year 1973 to 2001, and high

power is shown in this resonance period. The phase

difference indicates that the sunspot numbers are

negative correlated with the precipitation from year

1973 to 1991, and positive correlated from year 1991

to 2001, with an abrupt change around year 1991.

Figure 1(c) is the cross wavelet power spectrum of

sunspot numbers and average annual precipitation in

Mengla. We can see that there is a resonance period

of 8-12a between them from year 1972 to 2003, and

high power is displayed in this resonance period. The

phase difference indicates that there is a positive

correlation between them in the resonance period.

Figure 1(d) is the cross wavelet power spectrum of

sunspot numbers and average annual precipitation in

Zhaotong. The sunspot numbers and precipitation

have an 8-10a resonance cycle from year 1980 to

1992, a 10-12a resonance cycle from year 1985 to

2006, and a 1a resonance cycle from year 1989 to

1991. Higher power is shown in the 8-10a and 10-12a

resonance cycles, and lower power is shown in the 1a

cycle. The phase difference indicates that the sunspot

numbers are negative correlated with the variation of

annual precipitation in Zhaotong during the

resonance period. Figure 1(e) is the cross wavelet

power spectrum of sunspot numbers and the annual

average precipitation in Gongshan. There is a 9-12a

response periodicity of sunspot numbers and annual

precipitation from year 1983 to 2005. High power is

displayed in this resonance period. The phase

difference indicates that sunspots are positive

correlated with the precipitation during the resonance

period. Figure 1(f) is the cross wavelet power

spectrum of sunspot numbers and annual average

precipitation in Lijiang. We can see that sunspot

numbers and average annual precipitation have an 8-

12a resonance period from year 1974 to 2006. High

power is shown in this resonance period. The phase

Figure.1 Cross wavelet power spectrum of sunspot numbers and precipitation at kunming (a), Pu’er (b), Mengla (c),

and Zhaotong (d), Gongshan (e), Lijiang (f), Shangri-La (g) meteorological station.

Application of Wavelet Analysis to Correlation Between Sunspot Activity and Precipitation in Yunnan Province

227

difference indicates that sunspots are positive

correlated with the variation of precipitation in

Lijiang during the resonance period. Figure 1(g) is the

cross wavelet power spectrum of sunspot numbers

and average annual precipitation in Shangri-La. The

sunspot numbers and precipitation have an 8-12a

resonance cycle from year 1989 to 2007, and it shows

high power in this resonance period. The phase

difference indicates that sunspots are positive

correlated with the annual precipitation in Shangri-La

during the resonance period. In conclusion, the

analysis shows that the periodic responses of sunspot

activity and annual average precipitation mainly

focus on 8-12a, and the corresponding response

periods pass the significance test at 95% level. The

cross-wavelet power spectrum of sunspot numbers

and annual average precipitation of seven

meteorological stations in Yunnan Province shows

that their resonance periods are consistent. It indicates

that the variation of annual average precipitation is

related to solar activity. From the phase angle of

arrows in figure 1, it can be seen that there is a time

lag relationship between the average annual

precipitation and the solar activity index.

3.2 Result of Time Lag Correlation

Analysis

The response of time series often occurs lead or lag

phenomenon. This paper uses this method to study

whether there is a certain time lag relationship

between the two series. Figure 2 is the result of time

lag correlation analysis between sunspot numbers and

precipitation in Yunnan Province. The time lag

correlation analysis shows that the average annual

precipitation of Kunming, Pu'er, Mengla and

Gongshan meteorological stations lag the sunspot

numbers. The lag time are 9 years, 3 years, 7 years

and 8 years. The correlation coefficients are -0.22,

0.23, 0.2 and 0.12 respectively. The average annual

precipitation of Zhaotong, Lijiang and Shangri-La are

6 years, 8 years and 9 years ahead of the sunspot

numbers. The correlation coefficients are 0.22, 0.31

and 0.2 respectively. The results of the time lag

Figure.2 Time lag correlation analysis between sunspots and precipitation at kunming (a), Pu’er (b), Mengla (c), and

Zhaotong (d), Gongshan (e), Lijiang (f), Shangri-La (g) meteorological station.

ISAIC 2022 - International Symposium on Automation, Information and Computing

228

correlation analysis are basically consistent with the

wavelet analysis except the Zhaotong meteorological

station. It may be caused by the large number of

missing values in the data of the Zhaotong

meteorological station. The figure of the time lag

correlation analysis at Shangri-La meteorological

station is different from other meteorological station,

this may be due to the fact that the Shangri-La region

is part of the Three Rivers area, where the water

distribution has a greater effect on precipitation than

sunspot numbers. This method illustrates the

correlation and time-lag characteristics between

sunspot activity and precipitation.

4 CONCLUSIONS

This paper studies the periodic variation

characteristics of solar activity and precipitation at

seven meteorological stations in Yunnan Province

and analyzes the correlation between time series

based on wavelet analysis and time lag correlation

analysis. The main conclusions are as follows.

 Based on the cross-wavelet analysis, we study

the periodic responses of sunspot numbers and

average annual precipitation at seven

meteorological stations in Yunnan Province.

The results show that the periodic responses of

sunspot activity and average annual

precipitation are mainly concentrated in 8-12a,

and the response periodicity has significant

characteristics in the high-power region. From

the phase angle, we can see that there is a certain

lead-lag relationship between sunspot numbers

and average annual precipitation in Yunnan

Province. The seven meteorological stations are

selected from different climate zones, which

indicates that solar activity greatly influences

the annual precipitation in different climate

zones, and there is a good correlation between

them.

 Based on the time lag correlation analysis, we

find that the average annual precipitation of

Kunming, Pu'er, Mengla, and Gongshan

meteorological stations all lag the changes in

sunspot numbers. The average annual

precipitation of Zhaotong, Lijiang, and Shangri-

La meteorological stations is ahead of the

changes in sunspot numbers. They are basically

consistent with the results of the cross-wavelet

analysis. However, the correlation coefficient

between sunspots and the annual average

precipitation in different meteorological

stations is different, indicating that the response

of annual average precipitation to solar activity

in different regions is inconsistent.

ACKNOWLEDGEMENTS

This work is supported by Yunnan Academician

Workstation of Wang Jingxiu (202005AF150025),

the National Natural Science Foundation of China

(No. 11863002), and Sino-German Cooperation

Project (No. GZ 1284). We thank Wen Chen for the

help of this paper.

REFERENCES

Li, H, J., Gao, J, E., Zhang, H, C., et al. 2017. Response of

Extreme Precipitation to Solar Activity and El Nino

Events in Typical Regions of the Loess Plateau[J].

Advances in Meteorology, 2017:1-9.

Li, Y., Wen, Y., Lai, H., et al. 2020. Drought response

analysis based on cross wavelet transform and mutual

entropy[J]. AEJ - Alexandria Engineering Journal, 59:

1223-1231.

Zhao, Y., Luo, Y., 2021. Wavelet Analysis on Temperature

and Precipitation Changes in Dabie Mountain of West

Anhui[J]. Journal of Physics: Conference Series,

1732(1): 012105.

Cheng, S, B., Argaud, J, P., Iooss, B., et al. 2021. Error

covariance tuning in variational data assimilation:

application to an operating hydrological model[J].

Stochastic Environmental Research and Risk

Assessment, 35: 1019-1038.

Wang, B., Wang, Y., 1996. Temporal Structure of the

Southern Oscillation as Revealed by Waveform and

Wavelet Analysis[J]. Journal of Climate, 9(9): 1586-

1598.

Chellali, F., Khellaf, A., Belouchrani, A., 2010. Wavelet

spectral analysis of the temperature and wind speed

data at Adrar, Algeria[J]. Renewable Energy, 35(6):

1214-1219.

Alperovich, L., Zheludev, V., Hayakawa, M., 2016. Use of

wavelet analysis for detection of seismogenic ULF

emissions[J]. Radio Science, 38(6): 1-13.

Torrence, C., Webster, P, J., 2010. Interdecadal Changes in

the ENSO–Monsoon System[J]. Journal of Climate,

12(8): 2679-2690.

Ge, Z., 2007. Significance tests for the wavelet power and

the wavelet power spectrum[J]. Annales Geophysicae,

25(11): 2259-2269.

Banerjee, S., Mitra, M., 2014. Application of Cross

Wavelet Transform for ECG Pattern Analysis and

Classification[J]. IEEE Transactions on

Instrumentation and Measurement, 63(2): 326-333.

Grinsted, A., Moore, J, C., Jevrejeva, S., 2004. Application

of the cross wavelet transform and wavelet coherence

to geophysical time series[J]. Nonlinear Processes in

Geophysics, 11(5/6): 561-566.

Application of Wavelet Analysis to Correlation Between Sunspot Activity and Precipitation in Yunnan Province

229