
Inter-Provincial Trade and Resource Curse: A Study Based on GMM
Method
Tingting Zheng
1,* a
and Shanwen Cao
2b
1
North China University of Technology, Beijing, China
2
China Unicom Research Institute, Beijing, China
Keywords: Inter-Provincial Trade, Resource Curse, GMM.
Abstract: Objective: To verify the impact of inter-provincial trade on the resource curse. Process: Use GMM estimation
to systematically test the data from 1997 to 2019 from different dimensions such as full sample, intensity,
region and time. Result: (1)From the full sample test, the inter-provincial railway freight transport will
increase the negative impact of resource industries on economic growth and aggravate the resource curse; (2)
From the strength and regional heterogeneity test, the inter-provincial trade will promote the economic growth
of the eastern region and the regions with low resource dependence, but make the central and western regions
and regions with high resource dependence fall into the resource curse trap; (3) Resource development will
promote the development of inter-provincial railway trade and fixed asset investment, but it will crowd out
innovation and human capital, and there is a potential crowding out effect on inter-provincial highway trade,
manufacturing, opening to the outside world, urban individual and private economy.
1 INTRODUCTION
China gives full play to its super large market
advantage and domestic demand potential, and
constructs a new development pattern of domestic
and international double circulation and mutual
promotion. Inter-provincial trade is important support
to realize domestic circulation, so it is necessary to
conduct in-depth study the role of regional economy.
The practice of world economic development
shows that the economic development of some
resource-rich areas is not always good, and even
compared with resource-poor areas, their
development is slower. This negative correlation
between natural resources and economic
development is called the "resource curse"
phenomenon (Auty, 1993), and remains one of the
key issues of academic research since its inception.
A large number of scholars have discussed the
causes of the resource curse from different levels and
formed many insights and policy implications,
including: (1) The Dutch disease effect (Arezki &
Ismail, 2013); (2) Extruding effect (Li et al., 2020);
(3) System weakening effect (Zhan et al., 2021). (4)
a
https://orcid.org/0000-0003-2338-4444
b
https://orcid.org/0000-0003-2377-4000
Bad conditions of trade (Al-Shammari & AL-Obaid,
2018
)
, etc. The deterioration of trade conditions
theory mainly focuses on international trade, the
exchange of regional products, namely inter-
provincial trade, is ignored. This is not in line with the
practical model of "double cycle" of China's current
economic development. Inter provincial trade has two
impacts on regional economy: (1) Improve the
competitiveness of local economy. Inter provincial
trade can ease the local economic fluctuations,
improve the efficiency of resource allocation, and
then improve the comparative advantage of China's
products, achieve economies of scale, reduce
production costs, and improve the international
competitiveness of the industry. And as time goes on,
the contribution of inter provincial trade to the
regional economy will continue to increase, and the
role of inter provincial trade in regional economic
development will also be increasingly enhanced. (2)
Widen the regional economic gap. The asymmetry
and imbalance of inter provincial trade in terms of
outflow and inflow are not conducive to the
coordinated development of China's regional
economy. The eastern region requires open markets,
Zheng, T. and Cao, S.
Inter-Provincial Trade and Resource Curse: A Study Based on GMM Method.
DOI: 10.5220/0012028400003620
In Proceedings of the 4th International Conference on Economic Management and Model Engineering (ICEMME 2022), pages 221-227
ISBN: 978-989-758-636-1
Copyright
c
2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
221

while the central and western regions require closed
markets to enhance their economic initiative in China.
The benefits of China's interregional trade are mostly
obtained by developed regions, while the
underdeveloped regions benefit little from such trade,
even suffer damage to varying degrees.
Taking coal, oil and gas, non-metallic mining and
other resource industries as examples, in the input-
output analysis method, through the calculation of
intermediate input rate and intermediate demand rate,
these resource industries are intermediate product
based basic industries, with large intermediate
demand rate and small intermediate input rate. That is
to say, in the development process of these industries,
their dependence on other industries is relatively low.
On the contrary, their products are used as
intermediate inputs of other industries, resulting in
great demand from other industries. During the
development of the coal industry, in addition to the
local production, the use of intermediate products is
more from the purchase from other provinces. In
addition, the products produced by the coal industry
may also flow out, which has not played a real role in
promoting regional economic growth (Xiang &
Meng, 2011).
As China's economy enters a stage of high-quality
development, investment and export can no longer
effectively promote the high-quality development of
China's economy. China has vast territory, and the
division of labor and trade among various provinces
is enough to support high-quality economic
development. However, it is unclear whether, for
resource-rich provinces, inter-provincial trade will
aggravate the local resource curse. Therefore, it is
necessary to clarify the impact of inter provincial
trade openness on regional economic growth, and on
this basis, study whether the development of
resource-based industries is a blessing or a curse to
regional economic growth, and to what extent.
2 VERIFICATION OF THE
IMPACT OF
INTER-PROVINCIAL TRADE
ON THE RESOURCE CURSE
In view of the lack of data on domestic inter-
provincial trade volume, only inter-provincial freight
volume can best represent inter-provincial trade, so
from the inter-provincial freight volume, data from
1997-2019 from 30 provincial regions were used to
re-verify the impact of inter-provincial trade on the
resource curse.
2.1 Model Selection
In order to further analyze the influence degree of
inter-provincial trade in resource industry on regional
economy, this paper constructs the following panel
model to verify the relationship between resource
dependence and economic growth. The specific
formula is as follows:
Y
i,t
=α+β
1
ED
i,t
+β
2
Intra
i,t
+θ
1
Res
i,t
+θ
2
Hum
i,t
+θ
3
Pe
i
,t
+θ
4
Made
i,t
+θ
5
Fiv
i,t
+θ
6
Tra
i,t
+η+μ+ξ
i,t
(1)
Y (Economic growth rate) is calculated from the
per capital GDP growth rate. Ed (Resource
development intensity) is measured by the proportion
of energy production to total national production.
Intra (Inter-provincial trade) is measured by the
proportion of inter-provincial railway trade (TL) and
inter-provincial highway trade (GL). Res
(Technology innovation investment level) is
measured by the proportion of financial technology
allocation in total fiscal expenditure. Hum (Human
capital accumulation level) is measured by the
proportion of students in ordinary middle schools. Pe
(Urban private and individual economic development
level) is measured by the proportion of urban private
and individual-employed people in the total number
of people employed. Made (Manufacturing
Development Level) is measured by the proportion of
manufacturing employees in total employment. Fiv
(Material capital investment level) is measured by the
proportion of the total social fixed asset investment in
GDP. Tra (Intensity of opening) is measured by the
proportion of total import and export trade in GDP,
among which the total import and export trade is
converted by the annual exchange rate over the years.
2.2 Test Results of the Whole Sample
First, all models were suitable for fixed effects by F
test, LM test and Hausman test, and then the
endogeneity of the models was tested by DWH test,
which found the endogeneity of models 3 and 4.
Generalized matrix estimation (GMM) can
effectively solve the model endogeneity problem, and
it is more robust. The specific results of the GMM
estimation are detailed in Table 1. The first order
difference perturbation auto-correlation and second
order difference perturbation are unrelated
corresponding to model 3 and 4, and the P value of
Sargan test is greater than 0.1, indicating that the
selection of tool variables is valid. Detailed results are
analyzed as follows:
(1) The resource development intensity
coefficient in model 1 was -0.5056, which is
significant at 1%, indicating that resource
ICEMME 2022 - The International Conference on Economic Management and Model Engineering
222
development has a negative impact on economic
growth, but the lack of control variables, only as a
comparative reference.
(2) Models 2 and 3 show the effects of inter-
provincial railway trade and inter-provincial highway
trade on regional economic growth, respectively.
Both are significantly positive at the 1% level, and the
coefficient of inter-provincial highway trade is
greater than that of inter-provincial railway trade.
This shows that inter-provincial trade can promote
regional economic growth, and inter-provincial road
trade plays a greater role.
(3) After model 4 adds control variables, the
coefficient of resource development intensity
becomes-0.3633, which is significant at the level of
1%. However, the absolute value is significantly
lower than model 1, indicating that control variables
such as innovation and human capital can curb the
curse phenomenon to a certain extent.
(4) Model 5 adds inter-provincial railway trade,
whose model coefficient is -0.2995, but not
significant, indicating that inter-provincial railway
trade does not effectively promote regional economic
growth; the coefficient of resource development
intensity becomes-0.4237, significant at 1%.
Compared with model 4, resource development
intensity coefficient increases, and innovation,
human capital, urban private and individual economy
coefficient is greatly reduced, shows that inter-
provincial railway trade not only not effectively
promote regional economic growth, but squeezed out
the other elements of promoting economic growth,
exacerbated the regional resources curse.
(5) Model 6 added inter-provincial highway trade
with a coefficient of 0.1767, significant at 5%, which
indicates that the resource development intensity
coefficient is -0.1911, despite the absolute increase, it
shows that inter-provincial highway trade can slow
down the regional resource curse.
The above analysis shows that inter-provincial
railway transportation will aggravate the negative
impact of regional resource development intensity on
economic growth, while inter-provincial highway
transportation will weaken the negative impact of
resource intensity on economic growth. The possible
reason is that the regional industrial structure causes
different modes of transportation. Primary resource
products represented by coal in transportation are the
way of railway transportation, and due to the
requirements of clean transportation, "coal", "ore"
highway transportation resources is banned, railway
freight more on behalf of the regional resources, the
increase of railway freight volume represents the
region out more resource products, illustrates the
regional industry is still concentrated in the
development of resources, such as a single heavy
industry.
To ensure the robustness of the test results, this
paper replaces the resource development intensity
expressed by the employee ratio Rd to estimate the
resource development intensity. The specific results
are shown in model 7 and model 8. The coefficients
of the core explanatory variables did not change
greatly, which shows that the test in this paper is
robust.
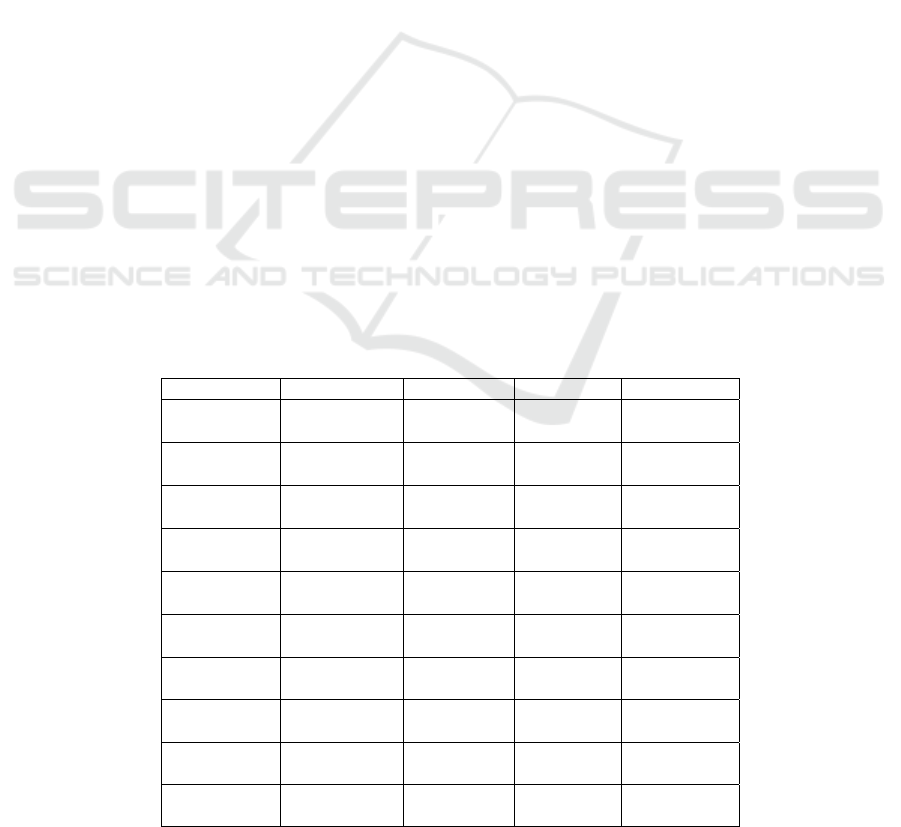
Table 1: Effects of inter-provincial trade on the regional resource curse (model 1-4).
variable model 1 model 2 model 3 model 4
Ed/Rd
-0.5056*
(-3.02)
-0.3633*
(6.26)
Tl
0.1517*
(7.61)
Gl
0.5224*
(13.40)
Res
0.7162*
(3.06)
Hum
0.7674*
(5.80)
Pe
0.2137*
(2.64)
Made
0.5839**
(
2.22
)
Fiv
0.5164*
(10.74)
Tra
0.4918*
(11.07)
cons
9.38
(
37.24
)
Inter-Provincial Trade and Resource Curse: A Study Based on GMM Method
223

R2 0.23 0.31 0.23 0.64
F
8.73
(
0.00
)
20.6
(
0.00
)
35.54
(
0.00
)
23.05
(
0.00
)
LM
210.43
(0.00)
266.24
(0.00)
487.08
(0.00)
451.4
(0.00)
Hausman
test
36.91
(0.00)
130.33
(0.00)
92.31
(0.00)
44.28
(0.00)
model FE FE FE FE
Note: t value in parentheses,
*, * *, * * *
are significant at 1%, 5% and 10% respectively, the same below.
Table 2: Effects of inter-provincial trade on the regional resource curse (model 5-8).
variable model 5 model 6 model 7 model 8
Ed/Rd
-0.4237*
(-4.45)
-0.1911***
(-1.72)
-0.1264*
(-2.81)
-0.5237*
(-4.45)
Tl
-0.2995
(-1.52)
-0.5447***
(-1.75)
Gl
0.1767**
(2.81)
0.3992*
(3.74)
Res
0.2772
(0.39)
0.7391**
(2.56)
0.1431*
(2.86)
0.6610
(1.05)
Hum
0.1653*
(12.69)
0.6610*
(4.79)
0.8707
(0.53)
1.2409
(0.22)
Pe
-0.0178**
(-2.56)
0.2409*
(3.22)
0.8677***
(1.86)
0.6128*
(3.14)
Made
0.6162
(
0.32
)
0.5128*
(
3.14
)
0.6539*
(
8.94
)
1.0713*
(
2.60
)
Fiv
0.7494*
(11.26)
0. 7013*
(12.60)
0.1886*
(3.28)
0.3204*
(3.64)
Tra
0.4018*
(
10.53
)
0.3204*
(
13.64
)
0.1858*
(
3.92
)
0.7494*
(
11.26
)
cons
9.47*
(34.62)
9.93*
(26.01)
9.31**
(22.49)
9.04*
(21.53)
R2 0.97 0.96 0.89 0.96
F
38.31
(0.00)
42.40
(0.00)
LM
441.98
(0.00)
388.29
(0.00)
Hausman test
105.29
(0.00)
91.9
(0.00)
DWH
6.05
(
0.00
)
5.95
(
0.01
)
AR (1)
-4.02
(
0.00
)
-4.21
(
0.00
)
AR (2)
0.14
(0.89)
-0.75
(0.453)
Sargan's test
2.22
(0.82)
3.80
(0.80)
model GMM GMM OLS OLS
ICEMME 2022 - The International Conference on Economic Management and Model Engineering
224
2.3 Resource-Dependent Strength
Heterogeneity Test
Due to the unbalanced distribution of resources in
China, there are also different resource dependence
strengths in different regions. Will the different
resource dependence strengths cause the different
effects of regional inter-provincial trade on the
regional resource curse? This paper introduces the
analysis in the form of virtual variables according to
the resource dependence heterogeneity. The specific
formula is set as follows:
Y
i,t
=α+α
1
ED
i,t
*RD+α
2
Intra
i,t
*RD+ηi+μ
i
+ξ
i,t
(2)
Among them, RD is the heterogeneity index of
resource development degree, which is calculated
according to the average resource development
intensity (the resource dependence intensity is
calculated by the ratio of employees in the mining
industry to all employees.) The 30 provinces are
divided into resource dependence group (RD
d
) and
resource development intensity group (RD
n
). When
investigating the group with high resource
dependency, set RD
d
to 1 and RD
n
to 0; When
investigating the low resource dependency group, set
RD
d
to 0 and RD
n
to 1. See Table 3 for specific
inspection results.
According to the Table 3, there is a large negative
impact on the high resource-dependence group, while
inter-provincial trade is not significant to the low
resource-dependence group, especially inter-
provincial trade. The main reason for this regional
heterogeneity is the difference in the structure of
cargo transfer and transfer. The areas with high
resource dependence strength are mainly transferred
from mineral resources and primary processing
products with low added value, and mainly rely on the
large batch transfer mode of railway transportation,
especially in the provinces with large coal resources.
State-owned coal enterprises in the transportation
process, although facing slightly higher railway
transportation costs, they still adhere to railway
transportation.
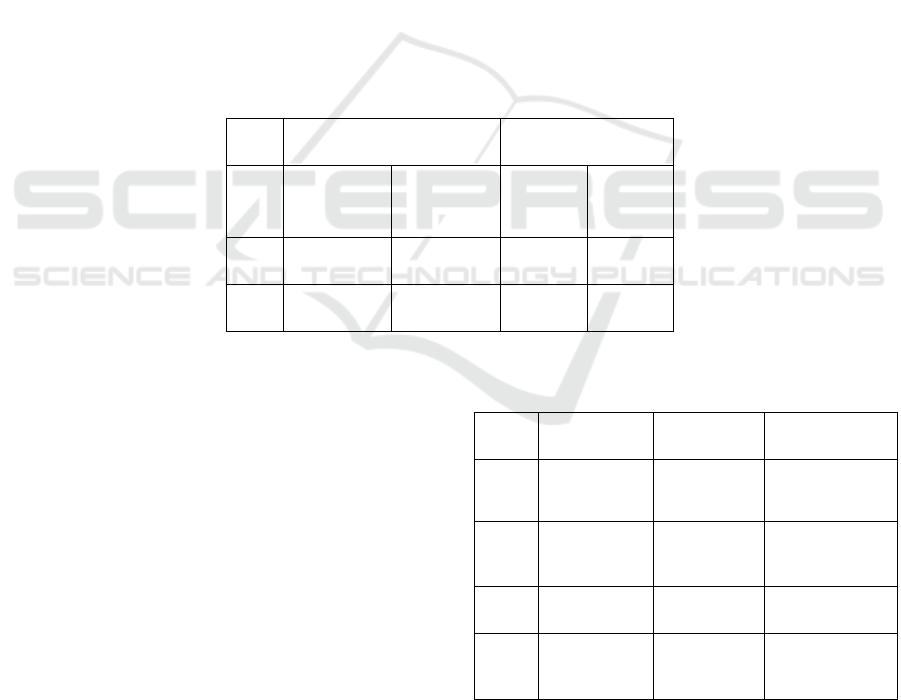
Table 3: Resource-dependent intensity heterogeneity in inter-provincial trade.
vari
able
high group low group
RD
-1. 4018
**
(-1.89)
-1.1008
*
(-2.77)
-0.0450
(-0.75)
0.0724
(0.04)
Tl
-0.6086
*
(-4.46)
0.7029
(1.22)
Gl
-0.0605
(1.21)
0.7926
*
(4.94)
2.4 Test of Regional Heterogeneity
In order to distinguish the different effects of inter-
provincial trade in the east, central and western
regions on the curse of regional resources, the
regional heterogeneity is also introduced in the way
of virtual variables. The specific formula is set as
follows:
Y
i,t
=α+α
1
ED
i,t
*area+α
2
Intra
i,t
*area+ηi+μ
i
+ξ
i,t
(3)
Among them, area is the regional heterogeneity
index. According to the regional distribution, 30
provinces are divided into three regions: eastern
(area
e
), central (area
m
) and western (area
w
). When
visiting the eastern region, set area
e
to 1, area
m
and
area
w
to 0, when visiting the central region, area
m
to
1, area
e
, area
w
to 0, when visiting the western region,
area
w
to 1, area
e
, area
m
to 0, specific test results are
shown in Table 4.
Table 4: Test of Regional Heterogeneity in Interprovincial
Trade.
varia
b
le
east middle west
RD
-0.6804
*
(-5.34)
-1.4027
*
(-4.67)
-2.8278
***
(-1.79)
Tl
0.1359
*
(10.69)
-0.0894
(-0.64)
-0.0338
*
(-2.47)
RD
-0.2576
(-1.59)
-0.4691
***
(-1.93)
-1.1354
***
(-1.92)
Gl
0.1003
*
(10.77)
-0.0045
(-0.41)
-0.0285
*
(-2.43)
As can be seen from Table 4, except for inter-
provincial highway trade in the eastern region, all
other tests show that the intensity of resource
development will hinder regional economic growth,
while inter-provincial trade in the eastern region has
Inter-Provincial Trade and Resource Curse: A Study Based on GMM Method
225

significantly promoted the regional economic growth.
Although the central region is not significant, inter-
provincial trade has a potential negative impact on
regional economic growth; inter-provincial trade on
regional economy is significant. Moreover, the
negative impact of inter-provincial railway trade in
central and western China on regional economic
growth is obviously stronger than that of inter-
provincial highway trade. The test results and
resource dependence intensity heterogeneity
inspection, the central and western regions of China
for resource-dependent areas, with minerals, energy
and other primary products or primary processing
products, need to enter industrial products from the
eastern region, lead to long-term inter-provincial
trade deficit, cannot effectively promote regional
economic growth, but further intensified the
dependence on resource development.
3 THE CROWDING OUT EFFECT
The formation of the resource curse is due to the
crowding out of other production factors to promote
economic development by the development of
resources. Next, this paper analyzes the relationship
between the intensity of resource development and
provincial trade by using the classic model to test the
transmission mechanism of the resource curse, and
also analyzes the crowding out effect of the intensity
of resource development on other factors. The
specific formula is as follows:
TRANS=β
0
+βED+βRGDP
t,i-1
+ε (4)
Where, TRANS is the transmission mechanism
variable, that is, the control variable above.
Table 5: Results.
Trans ED
Tl 0.5775*
(
15.17
)
Gl -0.1973
(
-0.36
)
Made -0.5219
(
-0.19
)
Hum -0.6270*(-3.63)
Fiv 0.7272*(-3.33)
Res -0.1659*(-3.73)
Tra -0.7071
(
-0.43
)
Pe -0.4726
(
-0.30
)
It can be seen from Table 5 that resource
development has a significant role in promoting inter-
provincial railway trade (0.5775), but it has no
significant impact on inter-provincial highway trade,
but the coefficient is negative (-0.1973), indicating
that resource development has a potential negative
impact on inter-provincial highway trade. That is,
inter-provincial trade is one of the transmission
mechanisms of the resource curse. This paper also
analyzes the impact of the intensity of resource
development on other transmission mechanisms. The
intensity of resource development will have a
significant crowding out effect on human capital and
innovation, but it has no significant impact on
manufacturing, opening up, urban private and
individual economic development, but there is a
potential crowding out effect.
4 CONCLUSIONS
The conclusions of this paper are as follows: (1) From
the full sample test, inter-provincial railway trade will
increase the negative impact of resource industries on
economic growth, further increase the dependence of
economies on resource factors, hinder the benign
growth of resource regions, and intensify the
"resource curse" effect;
(2) From the strength and
regional heterogeneity tests, Inter-provincial trade
will drive further economic growth in the east and
low-resource-dependent regions, But the Midwest
and highly resource-dependent regions will fall
into the "resource curse" trap; (3)
The crowding out
effect of resource development proves that resource
development will promote the development of inter-
provincial railway trade and fixed asset investment,
but it has a significant crowding out effect on
innovation, human capital and other production
factors, and there is also a potential crowding out
effect on inter-provincial road trade, manufacturing,
opening up, urban private sector and individual
economy.
ACKNOWLEDGMENT
Basic scientific research Funds of Beijing Municipal
Education Commission in 2020 (Project
No.:110052972027/131); Start-up funds for newly
introduced teachers from Northern University of
Technology (Project No.: 110051360002)
REFERENCES
Auty. R.M. Sustaining development in mineral economies:
the resource curse thesis. World Development,
1993(47): 62-74.
ICEMME 2022 - The International Conference on Economic Management and Model Engineering
226

Arezki R, Ismail K.Boom–bust cycle, asymmetrical fiscal
response and the Dutch disease[J]. Journal of
Development Economics, 2013, 101(10/94): 256-267.
AL-Shammari N, AL-Obaid S.Linkages of Global
Financial Crisis and Trade Direction in an Oil Based
Economy [J]. International Journal of Economics and
Financial Issues, 2018, 8(3), 250-259.
Xiang Rong Mei, Meng Yanju. Regional Input-output
Model Extension Study [M]. Southwestern University
of Finance and Economics Press. In September, 2011.
Yumei Li, Bushra Naqvi, Ersin Caglar, Chien-Chi Chu, N-
11 countries: Are the new victims of resource-curse?,
Resources Policy, Volume 67, 2020, 101697, ISSN
0301-4207.
Zhan Zhan et al. How exchange rate regimes are
exacerbating or mitigating the resource curse? [J].
Resources Policy, 2021, 72.
Inter-Provincial Trade and Resource Curse: A Study Based on GMM Method
227
