Option Pricing and Risk Hedging for High-Tech Company:

The Case for Apple

Minhsueh Chiang

1,†

, Jiaheng Xu

1,†

, Yuisam Law

2,*,†

and Renjie Yang

3,†

University of Illinois at Urbana-Champaign, United states

Jinan University, Guangdong, China

Zhuhai College of Jilin University, Guangdong, China

Keywords: Option Pricing, Apple, Black-Scholes.

Abstract: In this study, we examine the profitability of various hedging techniques for Apple stock options, which is

brand new to the field. The entire study is accomplished in two steps. In the first step, implied volatility is

determined and calculated by analyzing data on 10 different options on Apple stock, and the next step is to

construct a hedging portfolio based on the results of the first step, consisting of one unit of the specified option

and the underlying stock's delta shares. In summary, it has been determined that the hedging approach

investigated in this study has the potential to successfully cut risk. This study helps individual and institutional

investors to effectively construct a portfolio of Apple's stocks and select the most appropriate hedging

strategy. Use this as a reference. It should be noted that the Black-Scholes model used in this study has a zero-

interest rate assumption. In addition, the Black-Scholes model ignores the transaction costs that exist in real

markets; therefore, the results of this model may not be fully accurate, but additional research in the near

future would be beneficial.

1 INTRODUCTION

In today's economy, there simply aren't any ways to

profit from price differences. In a world without risks,

there is a certain likelihood that the stock price would

increase, and this is known as the risk-neutral

probability. We do not, however, presume that all

market participants are risk averse or that high-risk

investments would provide returns equivalent to those

on safer investments. This theoretical value is a

measurement of the probabilities associated with

purchasing and selling the assets assuming all

probabilities were equal (Victoria, 2021). This is the

premise of the study for hedging.

In finance, hedging refers to the action of

protectingb your position, and or profit from the

potential risks (Cvitanic, 2004). No matter which

positions you take in the financial market, there will

always exist different kinds of risk referring to your

decision. It could be liquidity risk, interest rate risk,

and or default risk, depending on which financial asset

These authors contributed equally

†

Corresponding author

you chose to protect your current position. Thus,

financial derivatives were invented, and were utilized

to mitigate some of the risk that you might encounter.

Following on, within all these different kinds of

financial derivatives, options were most widely and

commonly used in hedging strategies. Option-hedging

strategies were one of the most well-known and

thoroughly studied strategy in the financial industry as

well.

To demonstrate, option hedging strategy first starts

when option contracts appear, in which option pricing

theory such as the Black-Scholes theory were also

investigated. Following on, different scholars started

to investigate in different option hedging strategies

that could outperform the market. For instance, Sami

Vähämaa studied the strategy which was called “Delta

Hedging with Smile”, which utilized the volatility

smile as one of the hedging components, and,

moreover, demonstrated a better performance on

hedging instead of delta hedging (Vähämaa, 2004).

Subsequently, there were also statisticians and

scholars such as Roland Langrock, Thomas Kneib,

Chiang, M., Xu, J., Law, Y. and Yang, R.

Option Pricing and Risk Hedging for High-Tech Company: The Case for Apple.

DOI: 10.5220/0012033600003620

In Proceedings of the 4th International Conference on Economic Management and Model Engineering (ICEMME 2022), pages 395-400

ISBN: 978-989-758-636-1

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

395

Richard Glennie & Théo Michelot who investigated in

“Markov-switching models”, which this statistical

model were then widely utilized in producing

Markov-switching deltas in different hedging

strategies as well (Langrock, 2017). Besides, many

scholars decided to study delta hedging with respect to

different kinds of options as well. For instance,

Alexander and Iryna decided to look for potential delta

hedging strategies in exotic options, based on “Price

trajectories are d-dimensional continuous functions

whose path wise quadratic variations and covariation

are determined by a given local volatility matrix”

(Schied, 2016).

On the other hand, researchers have dedicated

inspections on some fields. For instance, Jaska

Cvitanic and Ioannis Karatzas applied the continuous-

time model in order to do hedging for an arbitrary

contingent claim, with proportional transaction costs

(JAKSA, 1996). Also, Avellaneda Marco and ParaS

Antonio developed strategies, for the hedge of

derivative securities, under the presence of transaction

costs (AVELLANEDA, 1994).

However, limited research scrutinized the

performance of hedging strategies in companies’

sector. This paper will orient on such matter, selecting

Apple Inc. as our analysis target. Its leading position

in technology sector enables it to be a representative

company as chosen. In this study, results are given by

the act of delta hedging strategy applying the Black-

Scholes Model on Apple Inc.

This paper is organized as follows: Section 2 Data

and Method; Section 3 Result and Discussion; and

Section 4 Conclusion.

2 DATA AND METHOD

2.1 Data

The data used is all from Yahoo Finance

(https://finance.yahoo.com/). We choose the assets of

apple. The reason why we choose these assets as

follows Apple's products are consistently ranked

among the most sought after throughout the globe, and

the firm is now venturing into new areas of the

technology sector to provide even more ground-

breaking instruments and services, which means

Apple has made preparations to maintain its

competitive advantage. We choose five different call

options and put options that all mature on 2022 July

1st with different strike prices, to calibrate an implied

volatility. After that, a hedging strategy was

constructed for another option on Apple stock from

June 1st, 2022, to June 14, 2022. In detail, the option

contracts collected to calibrate the implied volatility of

Apple Inc. stock are shown in the table below.

Table 1: The 10 options chosen.

Call options chosen for calibration

Apple Inc.

AAPL220701C

00125000

AAPL220701C

00126000

AAPL220701C

00127000

AAPL220701C

00128000

AAPL220701C

00129000

Put options chosen for calibration

Apple Inc.

AAPL220701P0

0125000

AAPL220701P0

0126000

AAPL220701P0

0127000

AAPL220701P0

0128000

AAPL220701P0

0129000

And the option contract selected for Apple inc. for

hedging is shown in the table below.

Table 2: The option chosen for hedging.

Option selected for hedging

Apple Inc. AAPL220708C00125000

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

396

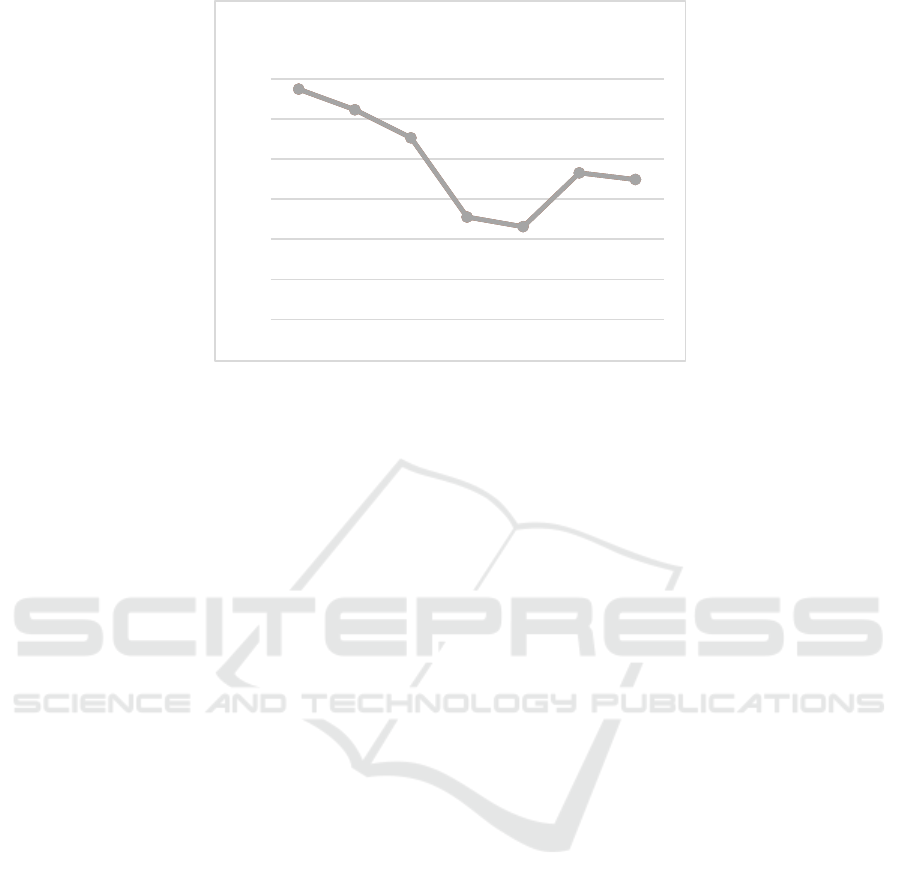
Figure 1. The stock price trend of Apple Inc.

As shown above, Apple Inc’s stock price had small

reduction from Jun. 1st, 2022, to Jun.28th,2022, from

$148.71 to $138.44. there was some minor volatility

as Apple's share price declined during the study

period.

2.2 Method

The Black-Scholes formula is used as a model for

valuing European or American call and put options on

a non-dividend paying stock. In option pricing theory,

the Black-Scholes equation is one of the most

effective models for pricing options (Mehrdoust,

2014). Black Scholes model take into account the risk

factor of the underlying stock, the strike price of the

option contract, the initial stock price and the time

value of money, which are all significant factors,

while pricing each option contract. Its

comprehensiveness and completeness also enhances

its accuracy while computing different option prices.

All options have limited downside and rely on price

volatility for upside, thus a rise in volatility raises the

value of both calls and puts (Yacine, 2003). However,

the Black Scholes model, similar to other option

pricing models, is not a perfect one as well. In fact,

there are some unrealistic assumptions that the Black

Scholes model makes in order for its convenience of

computation and conciseness. First, the Black Scholes

model assumes that volatility of the stock and the

market’s risk-free rate are all constant throughout the

whole maturity time, which is not true in the real case.

Second, the Black Scholes model also assumes that no

option could be exercised before the maturity time,

which makes it only effective while pricing European

option contracts. Third, the Black Scholes assumed

that the market is a frictionless one, which means there

would not exist any transactional costs while trading

these financial derivatives, which is also unrealistic,

too. Last but not least, although all these up-mentioned

assumptions might affect the accuracy of the Black

Scholes model, we could not deny that it is still one of

the most common and conservative way for pricing

European option contracts.

Options Spread is a trading strategy for options in

the financial market that entails taking opposite

directional positions in the price of a pair of options

belonging to the same asset class but with different

strike prices and expiry dates. A spread position

involves two options with distinct strike prices and

expiry dates (Abhilash, 2021). The hedging strategy is

completed with two steps in the research as below.

First, the implied volatility of the stock is calibrated

with the price of the stock and that of ten options as

selected, on the stock using Black Scholes model.

Second, applying the implied volatility calculated, a

hedging strategy is constituted for a chosen option on

the stock.

Following on, the implied volatility utilized in the

Black-Scholes model is an estimated value estimated

by calculating the market stock prices’ standard

deviation or other estimating and forecasting

techniques such as maximum likelihood estimation,

moment estimation, generalized linear model,

Bayesian point estimation. In our study, we decided to

estimate the volatility in two different ways: the

traditional market stock prices’ standard deviation and

minimizing the difference between real market option

price and Black-Scholes price calculated utilizing the

Black-Scholes formula. The whole pricing process

stars as the following. First, we choose the 2022 June

1st AAPL open price as our initial stock price S (0).

Second, we choose five different call options and put

120

125

130

135

140

145

150

6,01 6,06 6,09 6,14 6,17 6,23 6,28

Appe Inc.

Option Pricing and Risk Hedging for High-Tech Company: The Case for Apple

397

options that all mature on 2022 July 1st with different

strike prices. After we finish computing our Black-

Scholes price for every option, we start calibrating our

standard deviation. As mentioned, we first calibrated

our sigma by calculating the standard deviation

between the market stock prices from May 1st to May

31st. The second way is to calculate the sum of

squared errors between the BSM options prices and

the real-market option prices calculated for every

option from June 1st, 2022, to July 1st, 2022.

Subsequently, the sum of squared errors for the 10

options for the AAPL stock are minimized to calibrate

the most accurate implied volatility. Third, we plug in

these numbers into the Black-Scholes formula listed

below with t representing the time to maturity, the

time difference between July 1st and June 1st, S(t)

representing the initial stock price, K representing the

strike prices, 125 to 129, and representing the risk-free

interest rate, which is assumed to be 0 for

computational conveniency. In the Black-Scholes

formula, we have to first compute 𝑑



and 𝑑



as the

following equation.

𝑑



σ√(𝑡)

ln

𝑆

(

𝑡

)

𝐾

+𝑟+



𝑡

(1)

𝑑



σ√(t)

ln

𝑆

(

𝑡

)

𝐾

+𝑟−



𝑡=𝑑



−σ

√

(2)

Following on, we have to plug d_1 and d_2 into

the normal distribution operator in order to calculate

its associating probability. Lastly, we can implement

the European Call option pricing formula under

Black-Scholes in the following.

𝐶𝑡,𝑆

(

𝑡

)

=𝑆

(

𝑡

)

𝑁

(

𝑑



)

−𝐾𝑒



𝑁

(

𝑑



)

(3)

Similarly, for the price of the put option, we can

calculate it by either the Black-Scholes formula listed

below, or simply by implementing the Put-Call Parity

formula.

𝑃𝑡,𝑆

(

𝑡

)

=𝐾𝑒



𝑁

(

−𝑑



)

−𝑆

(

𝑡

)

𝑁(−𝑑



)

(4)

After we finished computing our Black-Scholes

price for every option, we start calibrating our

standard deviation. As mentioned, we first calibrated

our sigma by calculating the standard deviation

between the market stock prices from May 1st to May

31st. The second way is to calculate the sum of

squared errors between the BSM options prices and

the real-market option prices calculated for every

option from June 1st, 2022, to July 1st, 2022.

Subsequently, the sum of squared errors for the 10

options for the AAPL stock are minimized to calibrate

the most accurate implied volatility.

Table 3: Comparison for Statistical Indicators.

Sigma Call option Put option

SSE 61.3 59.59 1.71

Historical

Va lu e

7.9% 55.53 1.12

Following the implied volatility calibration, a

hedging strategy is created for a particular option on

the stock’s equity. First, the strike price and maturity

date for the selected option contract, as well as the

stock price information from 1st to 14th June 2022, are

collected. The prices of the selected option contract

are then determined by applying the Black Scholes

model and the calibrated implied volatility determined

by the aforementioned formula.

Day 1:

𝑃𝑜𝑟𝑡𝑓𝑜𝑙𝑖𝑜 𝑣𝑎𝑙𝑢𝑒(𝑡)=𝐶(1, 𝑆(1))

(5)

Day 2-14:

𝑃𝑜𝑟𝑡𝑓𝑜𝑙𝑖𝑜𝑣𝑎𝑙𝑢𝑒

(

𝑡

)

=𝑝𝑜𝑟𝑡𝑓𝑜𝑙𝑖𝑜 𝑣𝑎𝑙𝑢𝑒

(

𝑡−1

)

+𝑁(𝑑



)(𝑆

(

𝑡

)

−𝑆

(

𝑡−1

)

(6)

Second, the hedging portfolio consists of N(d1)

units of shares and one unit of a call option contract,

where N(d1) represents the delta for the BSM model.

The value of N(d1) on each day can be computed. The

methodology can be used to calculate the portfolio

value, loss or profit without hedging, and loss or profit

with hedging for each day between June 1 and June

14, 2022.

𝐿𝑜𝑠𝑠 𝑤𝑖𝑡ℎ𝑜𝑢𝑡ℎ𝑒𝑑𝑔𝑖𝑛𝑔(𝑡)

=𝑆

(

𝑡

)

−𝐾−𝐶(1,𝑆

(

)

(7)

𝐿𝑜𝑠𝑠 𝑤𝑖𝑡ℎℎ𝑒𝑑𝑔𝑖𝑛𝑔(𝑡)

=𝑆

(

𝑡

)

−𝐾

− 𝑝𝑜𝑟𝑡𝑓𝑜𝑙𝑖𝑜 𝑣𝑎𝑙𝑢𝑒(𝑡)

(8)

The effectiveness of the hedging strategy could be

evaluated in comparison across businesses and

industries as the loss or profit of the portfolio with or

without hedging is assessed.

3 RESULTS AND DISCUSSION

3.1 Results

In our study, after processing the comparisons of

profits or losses of the portfolio values with and

without hedging, from June 1st to June 14th, 2022, the

result shows obviously that the decision for holding

Apple Inc.’s option with hedging is more preferable,

despite both strategies obtained negative outcomes

instead.

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

398

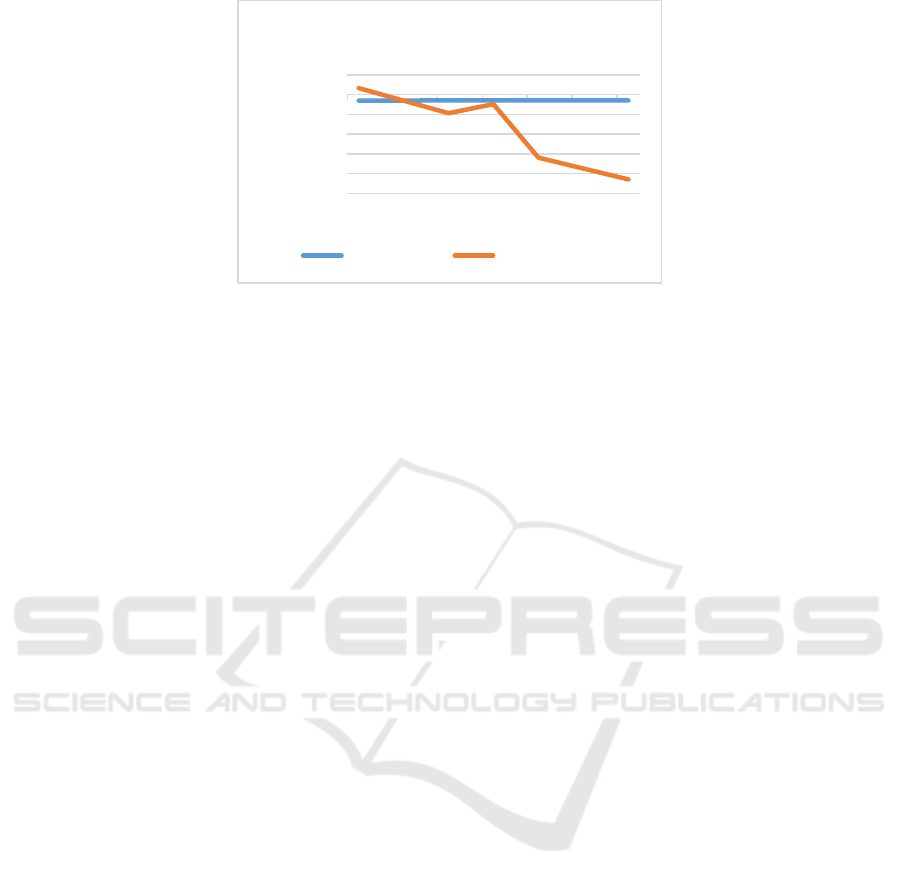
Figure 2: The comparison of the profit/loss holding one unit of the option on Apple Inc.’s stock with or without hedging.

The graph illustrates that the hedging strategy

completed better on the option on Apple Inc.’s stock.

With hedging, the loss is stable in the period; without

hedging, the loss declines rapidly within 10 working

days although there is a fluctuation in the middle. If

adding the profits and losses up for these 10 days, the

loss with hedging is $11.90, while that of without

hedging is $66.48. The differed amounts indicate the

hedging strategy has notably diminished the risk.

3.2 Discussion

The delta hedging strategy above-mentioned performs

pretty well on the Call option contract for the Apple

company and stock. We can tell that it has an

outstanding effect on helping us reduce and mitigate

our loss while investing in the Apple company’s stock

and option. In other words, the strategy implemented

in the study helped hedge the delta risk which is the

risk associated with the price movement of the

underlying stock of the option. Theoretically, delta

could also be defined as the derivative of the option

price with respect to the market price of the underlying

stock. In short, as we hold one unit of the option

contract, and delta shares of the underlying stock, the

portfolio reaches delta neutral, and thus, helps us

hedge the potential risk induced by the price

movement.

The Apple Inc Corporation is one of the most

essential companies not only in the technology sector,

but also in the US NASDAQ index. Moreover, the

Apple company is also one of the most actively traded

options, which also indicates that it would have more

complete and continuous data while implementing our

hedging strategy. Statistically speaking, more

continuous and complete data helps empower our

estimation and calculation of the volatility of the stock

and Black-Scholes option price. Moreover, in a

financial perspective, a more actively traded option

also enables the liquidity of our transaction and also

indicates that there would not be many options that are

far out of the money.

The Apple Inc’s has an average option trading

volume of four hundred thousand per day, which is

very liquid and commonly traded. Many other

technology companies such as Microsoft, Meta,

TESLA, and or Netflix also possess high trading

volume. In contrast, companies from the industrial,

financial and retail sectors do not trade in such large

volume, which also make these option contracts

difficult to liquidate. Therefore, for our Black-Scholes

model to be stable and complete initially, an option

which is commonly traded is an important factor.

Subsequently, a commonly traded option could also

enhance the accuracy of our volatility calibration and

Black Scholes option pricing. In sum, the Apple

company is a distinguished example which fit our

study needs and also perform well in our hedging

strategy.

4 CONCLUSION

This paper examines the performance of hedging

strategies for options on Apple stock. Although

researchers have studied hedging strategies using

options and sector-specific hedging strategies, the

topic discussed in this paper has not been studied

before. Therefore, in this paper, the delta hedging

strategy is used for options on Apple Inc. and its

hedging performance is analyzed. First, the implied

volatility is calibrated by using data from ten options

on this Apple stock. Then, based on the calculated

implied volatilities, a hedging portfolio was composed

containing one unit of a specific option and the

underlying stock's Delta shares. Finally, it is

calculated that the hedging strategy in this study

effectively reduces the risk. This study provides an in-

-20,00

-16,00

-12,00

-8,00

-4,00

0,00

4,00

6/2 6/4 6/6 6/8 6/10 6/12 6/14

Profit (Loss) ($)

Apple Inc.

with hedging without hedging

Option Pricing and Risk Hedging for High-Tech Company: The Case for Apple

399

depth analysis of the performance of Apple's stock

options using a hedging strategy, which helps

individual and institutional investors to effectively

build an Apple portfolio and choose the most suitable

hedging strategy, as well as being a reference for the

study of hedging strategies on other stocks.

It should be noted that the interest rate used in the

Black-Scholes model in this study is assumed to be

zero, and the Black-Scholes model also ignores the

transaction costs that exist in the real market, so the

results of the model may not be fully accurate and

deserve more research in the future.

REFERENCES

A. Schied, I. Voloshchenko. Pathwise no-arbitrage in a

class of Delta hedging strategies. Probab Uncertain

Quant Risk, 2016, 1(3).

https://doi.org/10.1186/s41546-016-0003-2

A. Yacine, D. Jefferson. Nonparametric option pricing

under shape restrictions. Princeton University, 2003

https://www.princeton.edu/~yacine/cnvx.pdf

C. JAKSA, K. IOANNIS. Hedging and Portfolio

Optimization under Transaction Costs: A Martingale

Approach. 1996, 133-165

C. Victoria.Option Pricing Model. FINANCIALEDGE,

2021 https://www.fe.training/free-resources/financial-

modeling/options-pricing-models/

F. Mehrdoust, M. Mirzazadeh. On analytical solution of the

black-scholes equation by the first integral method.

UPB Scientific Bulletin, Series A: Applied

Mathematics and Physics, 2014, 76.4, 85-90.

J. Cvitanic, Z. Fernando. Solutions Manual for Introduction

to the Economics and Mathematics of Financial

Markets. MIT Press, 2004.

M. AVELLANEDA, A. PA. Dynamic Hedging Portfolios

for Derivative Securities in the Presence of Large

Transaction Costs, Appl. Math. Finance, 1994, 165-

194.

R. Langrock, T. Kneib, R. Glennie, R. et al. Markov-

switching generalized additive models. Stat Comput,

2017, 27, 259–270. https://doi.org/10.1007/s11222-

015-9620-3

R. Abhilash. Risk Management Resources.

WallStreetMojo, 2021.

https://www.wallstreetmojo.com/options-spread/

S. Vähämaa. Delta Hedging with the Smile. Financial

Markets and Portfolio Management, 2004, 18, (3), 241-

255. Available at SSRN:

https://ssrn.com/abstract=796630

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

400