“I’s Dined with Ukraine”: Empirical Analysis on Consumer

Preference Change After Russo-Ukrainian War

Hanqi Ma

Princeton High School, Princeton, U.S.A.

Keywords: Russo-Ukrainian War, Bayesian Analysis, Latent Dirichlet Allocation.

Abstract: Recently, the Russo-Ukrainian war has become a major shock to the global market. This study investigates

the impact of conflict on consumer preference and consumer rationality with empirical analysis. This paper

applied the Difference-in-Difference method to measure the external shock’s (war) effect on Ukrainian and

Russian restaurants. The restaurants in the control group in the DiD model are selected with the

identification strategy of spatial matching. After eliminating the impact of Covid by controlling the Covid

Stringency Index as a covariate, the paper constructed a Bayesian structure time series Causal Impact

analysis on each Ukrainian and Russian restaurant visitor count to reflect the change in consumer preference

caused by the external shock. Then, the paper proposed the mechanism behind the changes in customer

visits by adopting a topic modeling approach - Latent Dirichlet Allocation and word cloud method to

analyze customer reviews of these restaurants on Yelp. The results showed that terms such as “Support” and

“Support Ukraine '' had become the trending words in Yelp comments since the start of the war, confirming

that consumers tend to show their support by dining in Ukrainian restaurants.

1 INTRODUCTION

The Russian-Ukrainian conflict has been a hot topic

on the international stage in the past century. When

wars or major pandemics occur, consumers change

their preferences and buying patterns in the short or

long term (Glick & Taylor, 2010). These consumer

behavioral changes could result in many more

consequences. One example is when the prohibition

caused by war from 1910 to 1933 caused less

alcohol consumption and a lower suicidal rate

(Zwanka & Buff, 2021). This paper is interested in

analyzing consumer preference change after the

outbreak of the war: whether people reacted

differently to Ukrainian and Russian products or did

it have no impact on consumer preferences. Because

product sale information is unavailable, consumer

flows in restaurants would be a preferred way of

research since foot-tracking data is available.

Therefore, this paper specifically analyzed the

consumer flow of Ukrainian and Russian restaurants

to investigate the war's effect on consumer

preference. Analyzing every restaurant across the

globe is impossible, so this paper focused on

restaurants in New York City. Sufficient data to

analyze are available for three Russian restaurants

(Mari Vanna, Anyway Cafe, Matryoshka) and four

Ukrainian restaurants (Veselka, Ukrainian East

Village Restaurant, Streecha, and Russian Samovar).

Russian Samovar is marked as a Russian restaurant

on Yelp. Still, this paper finds evidence indicating

that it is owned by a Ukrainian and has supported

Ukraine since the beginning of the war (Wasserman,

1989). Therefore, it is considered a Ukrainian

restaurant. These six restaurants have sufficient

raw_count and normalized_visits data from January

2021 to June 2022.

2 DATA

This study used the SAFE GRAPH data set, which is

collected from the physical world and makes

monthly updates to their data to assure the accuracy

of their dataset. The data is collected by identifying

device services with location components, as devices

with location services can be identified to determine

every user’s time spent at different locations. SAFE

GRAPH can account for the potential biases of

different types of devices and geographic biases.

SafeGraph tested for geographic bias by comparing

424

Ma, H.

“I’s Dined with Ukraine”: Empirical Analysis on Consumer Preference Change after Russo-Ukrainian War.

DOI: 10.5220/0012034100003620

In Proceedings of the 4th International Conference on Economic Management and Model Engineering (ICEMME 2022), pages 424-432

ISBN: 978-989-758-636-1

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

its determination of the state-by-state numbers of

home_location devices in the panel to the accurate

proportions reported by the 2016 US Census. The

result shows that the SafeGraph panel density

closely mirrors true population density, as the

overall average percentage point difference is < 1%,

with a maximum of +/-3% in each state.

Furthermore, SAFE GRAPH can eliminate potential

bias by collecting data from different cellular

carriers. The result shows that the data was collected

from 6 major carriers in the US.

Table 1: Shows the distribution of the six carrier types in the SAFE GRAPH dataset. The distribution shows that Verizon is

the most common carrier, and the distribution in the dataset is similar to the distribution on the public market.

Carrie

Count Ratio

Verizon 10,303,871 35.64%

AT&T 7,267,146 25.13%

T-Mobile 7,129,894 24.66%

rint 3,685,988 12.75%

Altice 323,221 1.11%

C-S

ire 204,800 0.71%

The dataset we used has 866188 rows and 48

columns, with each row representing a specific

location's data in a specific week. Some key

statistics this study used include raw_visit_ counts

and normalized _visits_by _total_visits, These

statistics were all collected and analyzed with

different methods, yet they all reveal the day-by-day

consumer flow to POI in New York City.

raw_visit_counts were collected by randomly

counting the number of visits to a POI. Normalized

data are more complicated and accurate for this

study than raw data because they analyze the portion

of visits or visitors in a POI compared to visits or

visitors in the New York region. Normalized data

will result in very small numbers, but they are more

accurate by limiting the potential impact from

external factors such as the general population flow

in the city.

3 DIFFERENCE-IN-DIFFERENCE

MODEL AND RESULTS

3.1 Model Specifications

To estimate the causal effect of the Russo-Ukrainian

war on the consumer preferences toward Ukrainian

and Russian restaurants, we formulate a panel

regression model entailing the restaurants of interest

and their weekly foot traffic before and after the war

through causal identification strategies. The method

aims to construct counterfactuals to estimate the

effect of an intervention due to the external shock.

By comparing the pre-intervention and post-

intervention data for both the control group and

experimental group, DiD can observe the outcome

trend after the intervention and can estimate an

external shock’s actual effect on the experimental

group. DID is a version of fixed-effect estimation

using panel data, e.g.:



= hypothetical consumers visits to Ukrainian

and Russian restaurants if the war did not occur



= actual consumers visits to Ukrainian or

Russian restaurants after the war occured



and γ



are both potential outcomes, but only

one of them can be observed in reality, i.e., γ



when

the war actually occurred. Therefore, using DID

allows to estimate γ



based on several assumptions:

the irrelevancy between outcome and intervention,

similar trend between control and experimental

groups in pre-intervention period, and that

exchangeability cannot be assumed between control

and experimental groups (Li, Wang & Zhong, 2022).

“I’s Dined with Ukraine”: Empirical Analysis on Consumer Preference Change after Russo-Ukrainian War

425

Figure 1: Difference in Difference graphical representation with linear regression.

In the study’s setting, the control group (blue) is

the non-Ukrainian/Russian restaurants, and the

experimental group (red) is the four Ukrainian or

three Russian restaurants. The DiD model enables us

to establish the counterfactual of the expected post-

intervention trend, and predict the intervention effect

by comparing it with the observed post-intervention

trend. Since DID is a fixed effect model, panel

regression can be used to estimate potential

outcomes along with dummy variables as the

following equation:



a



bγ



cX



ε



Where Y



is the number of visits to Ukrainian or

Russian restaurant i at week t, γ is the intervention

dummy variable that equals to 1 for Ukrainian or

Russian restaurants in post-intervention period, X is

dummy variables for fixed effects such as week and

placekey, and ε is the error term. This paper

compared the result by controlling for different

variables (week, placekey, or both) to validate the

consistency and significance of the result. For the

DID model, we counted 30 weeks before the first

day of the war (February 24, 2022) as the pre-

intervention period and 12 weeks after that as the

post-intervention period.

3.2 Results

We estimate the effect of war on raw visit counts for

the four Ukrainian restaurants shown in Table 2.

Overall, the results are consistent and robust when

both placekey and week fixed effects are included as

control variables, as the intervention effect is

estimated to be 9.40 (p<0.05). The adjusted R2 is

0.653, showing that the model successfully explains

65.3% of the observations. When only the placekey

is controlled, the result is still significant, with the

estimated intervention effect of 13.47 (p<0.01), and

the adjusted R-square to be 0.627. When the control

variable is none or week, the result failed to produce

a large adjusted R2, but it still yielded a strong and

significant intervention effect (p<0.001). The result

indicates that four Ukrainian restaurants had

received an average of 9.4 more customers. Given

that the calculated average number of raw_count

customers to the Ukrainian restaurant during the pre-

intervention period is 45.56, this means that

Ukrainian restaurants experienced a 20.6% increase

in customers just because of the Russo-Ukrainian

war.

Table 2: Raw_visit_counts DiD result for Ukrainian

restaurant customer flow.

Dependent

Variable

raw_visit_

counts

raw_visit_

counts

raw_visit_

counts

raw_visit_

counts

Model Pooled

OLS

Pooled

OLS

Pooled

OLS

Pooled

OLS

Interventio

n effect

31.695 *** 32.121 *** 13.466 ** 9.404 *

[7.323] [7.510] [4.741] [4.797]

Placekey No No Yes Yes

Wee

No Yes No Yes

Adjusted

0.051 0.052 0.627 0.653

# of Obs 942 942 942 942

Table 3 shows the result calculated with

normalized_visits_by_total_visits data for Ukrainian

restaurants, and it is very consistent with results

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

426

shown in table 2. When controlling both week and

placekey, the intervention effect is estimated to be

5.872e-7 (p<0.05) and adjusted R2 to be 0.641.

When the control variable is placekey, the

intervention effect is estimated to be 8.729e-7

(p<0.01) and adjusted R-square equals 0.642. When

the control variable is none or week, the intervention

effect is strong and significant, but the adjusted R2

is small, indicating the model is not a good fit to the

data. During the pre-intervention period, the average

number of normalized_visits is 2.849e-6, meaning

that 20.6% of more customers decided to eat in these

Ukrainian restaurants because of the effect of the

war.

Table 3 Normalized_visits_by_total_visits DiD result for Ukrainian restaurants customer flow.

Dependent Variable normalized_visits normalized_visits normalized_visits normalized_visits

Model Pooled OLS Pooled OLS Pooled OLS Pooled OLS

Intervention effect 1.932e-6 *** 2.004e-6*** 7.729e-7 ** 5.872e-7 *

[4.40e-7] [4.52e-7] [2.85e-7] [2.91e-7]

Placekey No No Yes Yes

Wee

No Yes No Yes

Adjusted R2 0.05 0.043 0.624 0.641

#of Obs 942 942 942 942

Table 4 shows the result generated from Russian

restaurants’ raw_visit_counts data. The result is very

similar to that of Ukrainian restaurants. When the

control variable is none or week, the intervention

effect is insignificant and the adjusted R2 proves the

model’s unfitness. But when placekey is being

controlled, the intervention effect of -2.655 (p<0.01)

becomes significant with the adjusted R2 to be 0.755

showing the model’s good fit. When both variables

are being controlled, the estimated intervention

effect is -3.597 (p<0.01) and the adjusted R2 equal

to 0.78. The average raw_count customers to the

Russian restaurants during the pre-intervention

period is 16.698, which means that the war caused a

21.5% decrease in consumer flow to Russian

restaurants.

Table 4: Raw_visit_counts DiD result for Russian restaurants customer flow.

Dependent Variable raw_visit_counts raw_visit_counts raw_visit_counts raw_visit_counts

Model Pooled OLS Pooled OLS Pooled OLS Pooled OLS

Intervention effect -3.094 -3.218 -2.655 ** -3.597 **

[1.727] [2.119] [1.018] [1.160]

Placekey No No Yes Yes

Week No Yes No Yes

Adjusted R2 0.003 -0.042 0.755 0.780

# of Obs 493 493 493 493

Table 5 shows the result calculated with

normalized_visits_by_total_visits data for Russian

restaurants, and it is different from the result on

table 4. When controlling both week and placekey,

the intervention effect is estimated to be -1.341e-7

and adjusted R2 to be 0.731, but it is not statistically

significant enough (p>0.05). When the control

variable is placekey, the intervention effect is

estimated to be -1.644e-7 (p<0.05) and adjusted R-

square equals 0.719. When the control variable is

none or week, the intervention effect is strong and

significant, but the adjusted R2 is small, indicating

the model is not a good-fit to the data. The average

number of normalized_visits to the Russian

“I’s Dined with Ukraine”: Empirical Analysis on Consumer Preference Change after Russo-Ukrainian War

427

restaurants during the pre-intervention period is

1.826e-6, which means that the war caused a 17.6 %

decrease in consumer flow to Russian restaurants

Table 5: Normalized_visits_by_total_visits DiD result for Russian restaurants customer flow

Dependent Variable normalized_visits normalized_visits normalized_visits normalized_visits

Model Pooled OLS Pooled OLS Pooled OLS Pooled OLS

Intervention effect -3.552e-7 ** -2.969e-7 * -1.644e-7 * -1.341e-7

[1.35e-7] [1.57e-7] [7.80e-8] [9.37e-8]

Placekey No No Yes Yes

Wee

No YesNoYes

Adjusted R2 0.006 -0.04 0.719 0.731

# of Obs 493 493 493 493

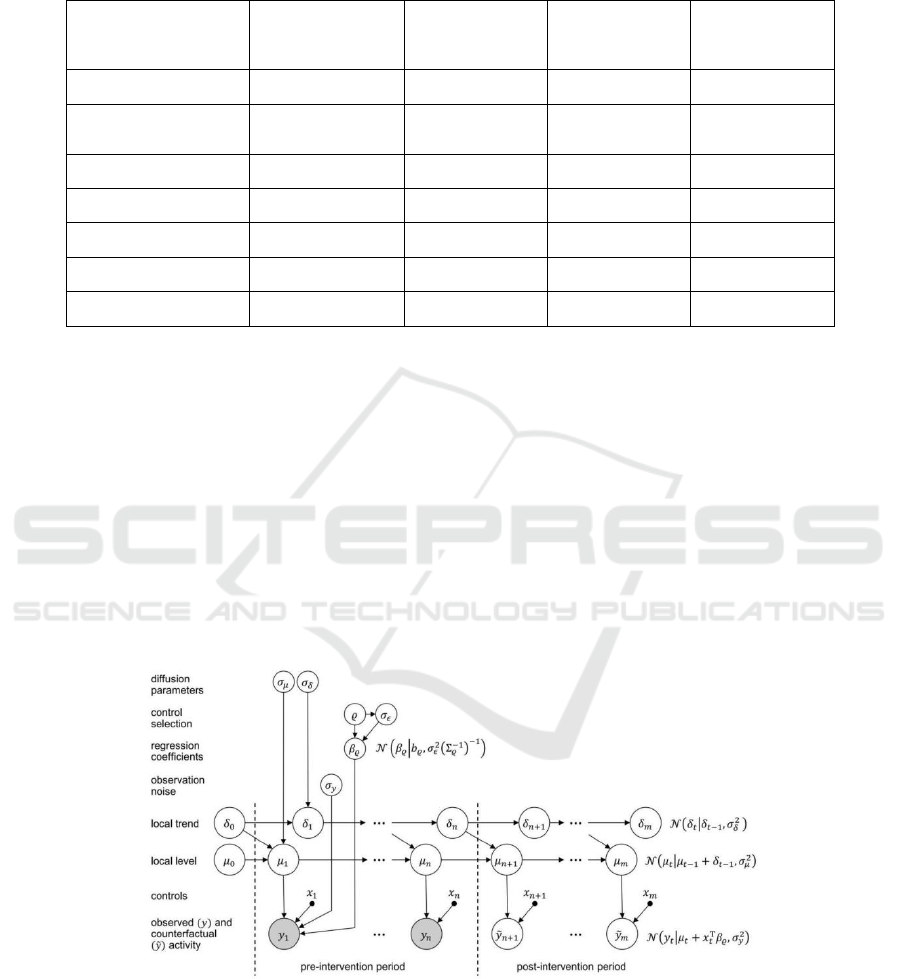
4 BAYESIAN STRUCTURAL

TIME SERIES MODEL AND

RESULTS

4.1 Model Specifications

This paper adopted the Bayesian Structural Time

Series Model and applied the Causal Impact analysis

on each individual Ukrainian and Russian restaurant

(Brodersen, Gallusser & Scott.,2015). This method

will predict a counterfactual on a time-series model

and predict an external shock’s intervention effect as

shown in Figure 2. The Russian Samovar restaurant,

although labeled as a Russian restaurant on Yelp,

was classified as an Ukrainian restaurant in this

study because most of its employees are Ukrainians.

The restaurant also showed its support to Ukraine

after the war happened (Alyson, 2022), such as

hosting fund-raisers or posting a blue and yellow

flag on the door and a sign that says, “Stand by

Ukraine. No War.”

Figure 2: Bayesian structure time-series model and Causal Impact methodology graphical representation.

In the real world, there is the observed data Y1,

and the goal is to estimate the counterfactual data

Y0, what would happen if the war never occurred.

Since there isn’t an actual experiment, the “control”

group doesn’t exist, so the goal of synthetic control

is to estimate something that just looks like a control

group (Abadie, Diamond & Hainmueller, 2015).

The difference between the counterfactual data

and observed data at time t is the intervention’s

effect. Constructing a Bayesian time-series model,

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

428

the Causal Impact method can estimate the post-

intervention trend by analyzing the pre-intervention

and controlling for certain fixed characteristics or

“covariates.” The Causal Impact model is based on

two important assumptions: 1) There is a controlled

time-series that is not affected by the intervention. 2)

The relationship between covariates and time-

series, established in pre-intervention, remains stable

throughout the post-intervention. In this study, the

covariate being used is the covid Stringency Index,

which measures the actual effect of Covid in New

York.

The Causal Impact model will produce some key

statistics such as the predicted customer count,

actual customer count, intervention absolute effect

and relative effect, their standard deviation, the

posterior tail-area p value, and each value’s 95%

confidence interval. The model also produces a

graph set showing the predicted vs. actual value,

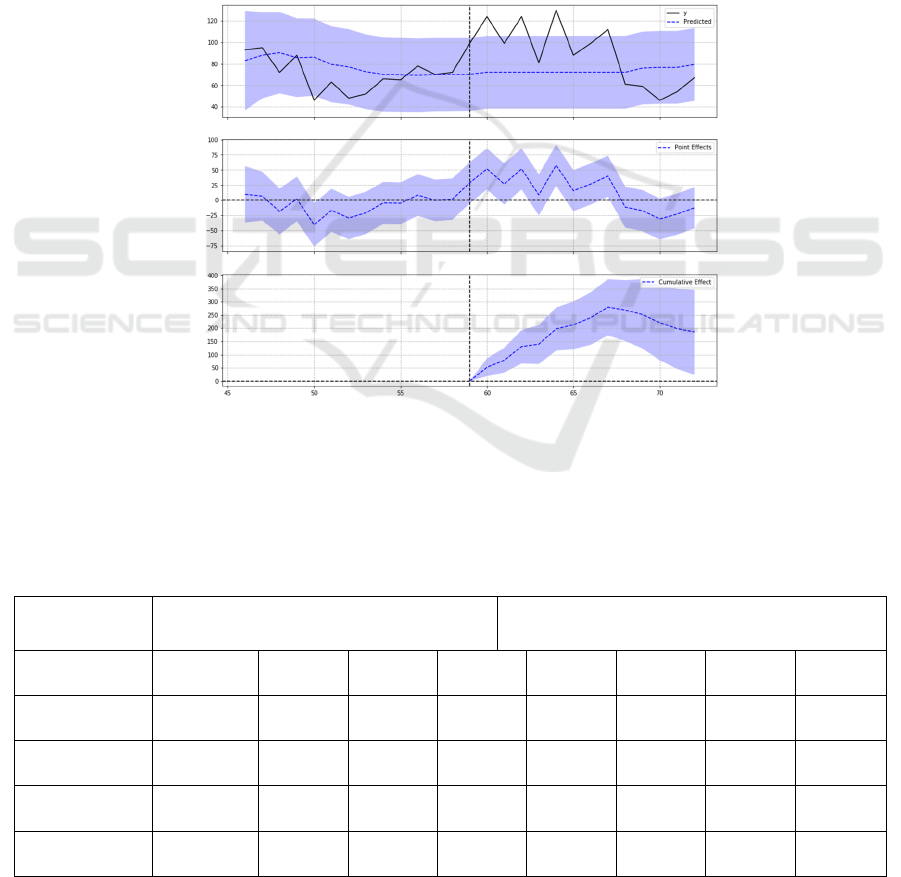
point effect, and cumulative effect. Figure 3 shows

the graphs produced with the raw_visit_counts of the

Ukrainian restaurant Vesekla. The first graph shows

the actual customer flow versus the predicted

customer 25 to 35 weeks before the war and 10

weeks after the war. The second graph shows the

point effect of y versus predicted over time. The

third graph shows the cumulative effect after the

intervention. A Bayesian structure time-series model

along with Causal Impact analysis will be applied to

each of the seven Ukrainian or Russian restaurants

to estimate the war’s effect on consumer preference

change.

Figure 3: Causal Impact graphing result for Veselka restaurant.

4.2 Results

Table 6 shows the result of causal Impact analysis

on Ukrainian restaurants. For each restaurant, the

patterns found in raw_visit_counts and

normalized_visits_by_total_vists are very similar.

Table 6: Bayesian structure time-series with Causal Impact result for Ukrainian restaurants.

Dependent

Variable

raw_visit_counts normalized_visits_by_total_visits

Restaurant number 1 2 3 4 1 2 3 4

Actual 88.0 15.62 19.8 110.3 0.53 0.1 0.14 0.69

Prediction 74.19 16.71 11.87 37.83 0.44 0.1 0.07 0.22

S.D. (4.53) (2.31) (3.88) (14.92) (0.02) (0.01) (0.02) (0.1)

Relative effect 18.61%*** -6.5% 66.8%*** 191.6%** 20.0%*** -4.9% 99.9%*** 215.2%***

“I’s Dined with Ukraine”: Empirical Analysis on Consumer Preference Change after Russo-Ukrainian War

429

S.D. (6.1%) (13.8%) (32.7%) (39.5%) (5.5%) (13.1%) (35.8%) (45.1%)

95% confidence

interval

[6.2%,

30.2%]

[-33.3%,

21.0%]

[4.0%,

132.2%]

[117.2%,

271.8%]

[9.5%,

31.2%]

[-30.8%,

20.6%]

[27.5%,

168.0%]

[128.6%,

305.4%]

Veselka (1)'s result shows that during the post-

intervention period, the response variable had an

average value of approx. 88.0. By contrast, in the

absence of an intervention, we would have expected

an average response of 74.19. In relative effect, the

response variable showed an increase of +18.6%.

The 95% interval of this percentage is [6.2%,

30.2%]. This means that the positive effect observed

during the intervention period is statistically

significant and unlikely to be due to random

fluctuations. The probability of obtaining this effect

by chance is very small (Bayesian one-sided tail-

area probability p = 0.0). This means the causal

effect can be considered statistically significant.

Streecha (2)’s result shows that during the post-

intervention period, the response variable had an

average value of approx. 15.62. In the absence of an

intervention, we would have expected an average

response of 16.71. In relative effect, the response

variable showed a decrease of -6.6%. The 95%

interval of this percentage is [-33.4%, 20.8%]. This

means that, although it may look as though the

intervention has exerted a negative effect on the

response variable when considering the intervention

period as a whole, this effect is not statistically

significant and so cannot be meaningfully

interpreted. The apparent effect could be the result

of random fluctuations that are unrelated to the

intervention. This is often the case when the

intervention period is very long and includes much

of the time when the effect has already worn off. It

can also be the case when the intervention period is

too short to distinguish the signal from the noise.

Finally, failing to find a significant effect can

happen when there are not enough control variables

or when these variables do not correlate well with

the response variable during the learning period. The

probability of obtaining this effect by chance is p =

31.1%. This means the effect may be spurious and

would generally not be considered statistically

significant.

Ukrainian East Village Restaurant (3)’s result

shows that the response variable had an average

value of approximately during the post-intervention

period. 0.14. By contrast, without intervention, we

would have expected an average response of 0.07. In

relative effect, the response variable showed an

increase of +99.9%. The 95% interval of this

percentage is [31.2%, 170.5%]. This means that the

positive effect observed during the intervention

period is statistically significant and unlikely to be

due to random fluctuations. The probability of

obtaining this effect by chance is very small

(Bayesian one-sided tail-area probability p = 0.0).

This means the causal effect can be considered

statistically significant.

Russian Samovar(4)’s result shows that during

the post-intervention period, the response variable

had an average value of approx. 110.3. By contrast,

in the absence of an intervention, we would have

expected an average response of 37.83. In relative

terms, the response variable showed an increase of

+191.6%. The 95% interval of this percentage is

[117.2%, 271.8%]. This means that the positive

effect observed during the intervention period is

statistically significant and unlikely to be due to

random fluctuations. The probability of obtaining

this effect by chance is very small (Bayesian one-

sided tail-area probability p = 0.0). This means the

causal effect can be considered statistically

significant.

Table 7: Bayesian structure time-series with Causal Impact result for Russian restaurants.

Dependent

Variable

raw_visit_counts normalized_visits_by_total_visits

Restaurant

numbe

5 6 7 5 6 7

Actual 29.23 3.42 7.0 0.18 0.02 0.04

Predicted 35.46 5.66 20.02 0.21 0.04 0.12

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

430

S.D. (2.79) (0.99) (2.39) (0.02) (0.01) (0.01)

Relative effect -17.6%** -39.7%*** -65.0%*** -15.3%* -42.6%*** -63.4%***

S.D. (7.9%) (17.5%) (11.9%) (8.4%) (17.1%) (11.6%)

95% confidence

interval

[-32.5%, -1.7%] [-75.9%, -7.3%] [-87.1%, -40.2%]

[-31.5%,

1.3%]

[-76.1%, -9.1%]

[-86.7%, -

41.3%]

Table 7 shows the result of causal Impact

analysis on Russian restaurants. For each restaurant,

the patterns found in raw_visit_counts and

normalized_visits_by_total_vists are also similar.

Mari Vanna (5)’s result shows that during the

post-intervention period, the response variable had

an average value of approx. 29.23. By contrast, in

the absence of an intervention, we would have

expected an average response of 35.46. In relative

effect, the response variable showed a decrease of -

17.56%. The 95% interval of this percentage is [-

32.54%, -1.7%]. This means that the negative effect

observed during the intervention period is

statistically significant. The probability of obtaining

this effect by chance is very small (Bayesian one-

sided tail-area probability p = 0.01). This means the

causal effect can be considered statistically

significant.

Matryoshka (6)’s result shows that during the

post-intervention period, the response variable had

an average value of approx. 3.42. By contrast, in the

absence of an intervention, we would have expected

an average response of 5.66. In relative effect, the

response variable showed a decrease of -39.65%.

The 95% interval of this percentage is [-75.95%, -

7.29%]. This means that the negative effect observed

during the intervention period is statistically

significant. The probability of obtaining this effect

by chance is very small (Bayesian one-sided tail-

area probability p = 0.0). This means the causal

effect can be considered statistically significant.

Anyway Café (7)’s result shows that during the

post-intervention period, the response variable had

an average value of approx. 7.0. By contrast, in the

absence of an intervention, we would have expected

an average response of 20.02. In relative terms, the

response variable showed a decrease of -65.03%.

The 95% interval of this percentage is [-87.08%, -

40.22%]. This means that the negative effect

observed during the intervention period is

statistically significant. The probability of obtaining

this effect by chance is very small (Bayesian one-

sided tail-area probability p = 0.0). This means the

causal effect can be considered statistically

significant.

To summarize, the Bayesian time-series model

significantly proved the change of consumer

preference through investigating the customer flow

on three Russian and three Ukrainian restaurants.

The only restaurant which failed to produce a

statistically significant result is the Russian

restaurant Streecha, with a p-value of 31.07% and

95% confidence interval of [-33.26%, 21.05%].

Even so, it’s almost certain to conclude, with the

result produced by the Causal Impact analysis, that

the consumer preference has been shifted by the

outbreak of Russo-Ukrainian war. The consumers, in

response to the war, are more willing to dine in

Ukrainian restaurants and reluctant to dine in

Russian restaurants.

5 DISCUSSION

The DiD and Causal Impact results have shown the

shift in consumer preference due to the impact of the

Russo-Ukrainian war. When controlling for

variables like week or placekey, the DiD model was

able to generate robust results to prove an

approximately 20.6% increase in customers to

Ukrainian restaurants and a 21.5% decrease in

customers to Russian Restaurants. The Bayesian

structure time-series model and Causal Impact

method specifically analyzed each restaurant. The

method produced statistically significant results for

three of the four Ukrainian restaurants showing the

war’s positive impact on customer flow.

Furthermore, the model successfully proved the

war’s negative impact on all three Russian

restaurants.

This paper, different from many other previous

studies, focuses on the micro-level impact of the

Russo-Ukrainian war. By investigating the customer

flow of Ukrainian and Russian restaurants in New

York City, the study successfully proved that the

war has a robust effect on changing people’s

consumer preferences. People in New York, for

instance, decided to dine in Ukrainian restaurants to

show their attitude and support toward the

Ukrainians. On the other hand, Russian restaurants

“I’s Dined with Ukraine”: Empirical Analysis on Consumer Preference Change after Russo-Ukrainian War

431

like Mari Vanna suffered customer losses and

decreased revenues. In some extreme cases, people

expressed their anger toward Russia by harassing

and threatening Russian people and their businesses

(Anne & Haleluya, 2022). Many restaurant owners

can also sense this change in consumer preference.

Some owners, for example, decided to rebrand their

restaurants from “Russian” to “Ukrainian” or

“Eastern European” to avoid customer losses

(Kailey, 2022). This phenomenon will not last short,

however. Consumer preference will likely continue

to change and favor Ukrainian products in the next

few years, especially given that the war is continuing

and showing no sign of calling a truce. This paper

also confirmed the result of previous research stating

that major crisis and international events, such as

covid, are likely to affect consumer behaviors and

activities (Anastasiadou, Chrissos & Karantza,

2020).

6 FUTURE INSIGHT AND

IMPROVEMENT

While the result produced by this research is robust

and convincing, there could still be some potential

flaws that might lead to errors. One limitation of this

research is the small sample size. Because of the

unavailability of sufficient data, the only observation

units are the seven restaurants in New York City.

For future research, more samples should be added

across different regions to confirm the result's

significance. Another way this research could be

improved is by adding more control variables. Many

factors could impact a restaurant's customer flow.

This research did not account for all the possible

factors and may have ignored some unfound

possibilities and confounding factors.

Future research could also use additional data to

examine each restaurant's influence level from the

war. Although this research confirmed the war's

impact on consumer preferences, it is uncertain why

some Ukrainian restaurants experienced higher

customer growth than others. Future research could

build on top and study some notable characteristics

of a restaurant that would determine its level of

influence from external shocks like war or covid.

REFERENCES

Abadie, A., Diamond, A., & Hainmueller, J. (2015).

Comparative Politics and the Synthetic Control

Method. American Journal of Political Science, 59(2),

495–510. http://www.jstor.org/stable/24363579

Alyson Krueger (2022), New York’s Russian Restaurants

Feel War’s Impact, New York Times,

https://www.nytimes.com/2022/03/08/nyregion/russia

n-ukraine-restaurants-new-york.html

Anastasiadou, E., Chrissos Anestis, M., Karantza, I. and

Vlachakis, S. (2020), "The coronavirus' effects on

consumer behavior and supermarket activities: insights

from Greece and Sweden", International Journal of

Sociology and Social Policy, Vol. 40 No. 9/10, pp.

893-907. https://doi.org/10.1108/IJSSP-07-2020-0275

Anne D'Innocenzio and Haleluya Hadero (2022) , Russian

businesses in US face backlash from war in Ukraine,

https://abcnews.go.com/Business/wireStory/russian-

businesses-us-face-backlash-war-ukraine-83502964

Brodersen KH, Gallusser F, Koehler J, Remy N, Scott SL.

Inferring causal impact using Bayesian structural time-

series models. Annals of Applied Statistics, 2015, Vol.

9, No.1,247-274.

http://research.google.com/pubs/pub41854.html

Ira M. Wasserman. (1989). The Effects of War and

Alcohol Consumption Patterns on Suicide: United

States, 1910-1933. Social Forces, 68(2), 513–530.

https://doi.org/10.2307/2579258

Kailey Broussard (2022), A restaurant serving Russian

food rebrands itself after Russia invades Ukraine,

https://www.npr.org/2022/03/21/1087806514/a-

restaurant-serving-russian-food-rebrands-itself-after-

russia-invades-ukraine

Li, W., Wang, A., Zhong, W., & Wang, C. (2022). An

Impact Path Analysis of Russo–Ukrainian Conflict on

the World and Policy Response Based on the Input–

Output Network. Sustainability, 14(14), 8672.

https://doi.org/10.3390/su14148672

Reuven Glick & Allen Taylor (2010). COLLATERAL

DAMAGE: TRADE DISRUPTION AND THE

ECONOMIC IMPACT OF WAR. The Review of

Economics and Statistics, 92(1), 102–127.

http://www.jstor.org/stable/25651393

Russel Zwanka & Cheryl Buff. (2021). COVID-19

generation: A conceptual framework of the consumer

behavioral shifts to be caused by the COVID-19

pandemic. Journal of International Consumer

Marketing, 33(1), 58–67.

https://doi.org/10.1080/08961530.2020.1771646

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

432